Applying Continuity and Bernoulli's Equation
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Streamlines
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's start by understanding the concept of streamlines. Who can explain what a streamline is?

Isn’t it a line that represents the direction of fluid flow at every point?

Exactly! Streamlines help visualize fluid movement. Imagine a series of small balls following the path of the fluid—those are our 'virtual fluid balls.'

So, do we always have to draw these streamlines before applying Bernoulli's equation?

Yes, it's crucial! It ensures we understand how the pressure and velocity change throughout the flow. Remember the mnemonic 'Flow Visual - Draw First, Apply Later' to help you recall this step.

What happens if we skip drawing them?

Not drawing them can lead to misunderstandings about the flow dynamics and may result in miscalculating pressures or velocities. So it’s like drawing a roadmap before a trip!

To summarize, streamlines represent the direction of flow and are essential for applying Bernoulli's equation accurately.
Understanding Bernoulli's Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's dive into Bernoulli's equation. Can anyone tell me the basic form of this equation?

It relates pressure, kinetic energy, and potential energy of a fluid.

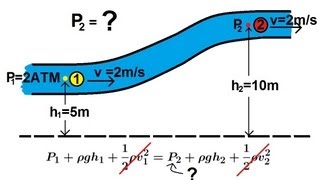
Correct! It can be written as: P + 0.5ρv² + ρgh = constant. The three components represent pressure energy, kinetic energy, and gravitational potential energy.

Why do we say it applies only to incompressible and frictionless flows?

Great question! Incompressibility assumes that the fluid density remains constant, which is valid at low speeds. Frictionless assumption means we ignore viscous effects, which isn't accurate near solid boundaries.

So, it has its limitations?

Yes, and misuse commonly occurs when those conditions aren’t met. Always assess the flow type when applying Bernoulli's equation.

To cap this off, remember, Bernoulli’s applications must be carefully considered with respect to their limitations.
Practical Application: Open Jet Problem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's solve a practical problem involving an open jet. How would we set this up using Bernoulli's principles?

We would apply the equation from the free surface to the jet exit.

Exactly! At the surface, the velocity is zero and pressure is atmospheric. At the exit, we have a velocity V and the pressure is also atmospheric.

How do we obtain the velocity from the height then?

Great! We deduce it using the energy conservation from Bernoulli's equation. The resulting relationship links the velocity to the height using V = √(2gh)! Remember this relation.

What if we introduce friction or any other real-world factors?

In such cases, we have to account for a discharge coefficient 'Cd' to apply corrections for energy losses. Always consider your flow conditions!

In summary, applying Bernoulli’s equation involves understanding how energy converts between pressure, kinetic energy, and potential energy, factoring in necessary adjustments.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, the principles of continuity and Bernoulli's equation are explained, emphasizing the need for understanding fluid flow along streamlines and recognizing its assumptions and limitations. The section highlights how these equations effectively quantify relationships between pressure, velocity, and energy in fluid systems, while cautioning against common misapplications.
Detailed
Applying Continuity and Bernoulli's Equation
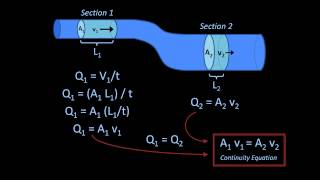
In fluid dynamics, the continuity and Bernoulli's equations are fundamental principles that aid in analyzing fluid motion. This section emphasizes visualizing fluid movement by sketching streamlines, which represent the flow paths of virtual fluid elements—referred to as fluid balls—traveling through different locations.
Key points include:
- Pressure and Energy Relationships: The pressure and velocity properties at two points dictate the energy transformations in fluid flow. In steady-state conditions, Bernoulli's equation allows for the computation of velocity based on pressure differences and potential energy changes due to height differences.
- Limitations of Bernoulli's Equation: While Bernoulli's equation is versatile, it has limitations. It is best applied under steady, incompressible, and frictionless flow scenarios. Misapplication can occur, especially in unsteady flows or near solid boundaries where viscous effects play a significant role. An implication of this is that while Bernoulli's equations can simplify many fluid mechanics problems, they also risk over-simplification, leading to potentially erroneous conclusions.
- Practical Applications: The example of an open jet shows how to derive relationships between exit velocity and fluid height using the Bernoulli equation. Important correction factors, such as the coefficient of discharge, are highlighted to compensate for real-world effects not accounted for in ideal models.
Overall, understanding the intricacies and assumptions of these equations is crucial for their correct application in engineering and fluid mechanics contexts.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Fluid Movement
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Similar way, the potential energy by this. So, if you it, instead of understanding or deriving along the streamlines, the same concept we can visualize it, if a virtual fluid balls is moving from one location to two locations, since it is a virtual fluid balls, again I am to talk about these, where we consider it is not a one fluid flow ball movements, we consider there are n number of fluid balls are there. They are having a pressure exiting one by others. Because of that, there will be a flow energy, which we quantify into pressure into area into delta x.
Detailed Explanation
In fluid dynamics, we can visualize fluids as 'virtual fluid balls' that travel along streamlines. Each 'ball' represents a group of fluid particles interacting based on pressure differences. This interaction results in energy flow, which is defined by the equation: Flow Energy = Pressure × Area × Distance. This means that as pressure changes, the energy associated with the flow also changes, showcasing how fluids behave in various conditions.
Examples & Analogies
Imagine a crowd of people (the fluid balls) moving through a narrow hallway (the streamline). The pressure with which they push against each other and the walls generates movement. If more people (higher pressure) enter the hallway, they move faster and create a flow of individuals much like how fluid movement is dictated by pressure differences.
Applying Bernoulli's Equation
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, we can say it, any fluid balls if you consider it, the flow energy per weight, the kinetic energy per weight, and the potential energy per weight, that is what is custom. So, this is the difference between a simple ball and the virtual fluid ball. So, what I am telling is that, whenever you apply the Bernoulli equation, you should draw the streamlines. You should visualize how the fluid moves.
Detailed Explanation
Bernoulli's equation relates the flow energy, kinetic energy, and potential energy of fluid to how they change along the streamline. It emphasizes the importance of visualizing the flow by drawing streamlines. Each point along a streamline needs to be analyzed to accurately apply Bernoulli's equation and understand how fluid velocity and pressure interact at different locations.
Examples & Analogies
Think of a water slide. As water flows down, it's similar to a 'virtual fluid ball'. The water at the highest point (potential energy) will eventually gain speed as it moves down (kinetic energy). If you visualize the slide as a streamline, you can predict how fast the water will be at various points along its path, which resembles the application of Bernoulli's equation.
Limitations of Bernoulli's Equation
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let us have a very quick, what are the limitations of Bernoulli equations. Bernoulli equations can be applied for unsteady flow, but the simplified derivations what you use it, those are for per steady flow. That means, there is no time component is there. And remember it, this equation is most frequently used, also misused equations, okay.
Detailed Explanation
Bernoulli's equation has limitations. It is primarily derived for steady, incompressible, and frictionless flow. When applying it to unsteady flows, like in real-life conditions, one must be cautious. Misuse often occurs due to misunderstandings about when and where the equation applies, which might lead to incorrect analyses.
Examples & Analogies
Imagine trying to use a detailed math formula for a specific scenario without considering the context. If you were to solve for the time it takes to finish a race at a steady pace, it wouldn’t work if the runner suddenly stopped then sprinted. Similarly, applying Bernoulli's equation without understanding its conditions can lead to errors in predicting how fluids behave.
Assumptions for Application
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The most important assumption is that the frictionless flow, that means it cannot be applied near to the solid. Because as you know it, whenever the fluid goes through near the solid, if there is a solid fixed surface, there will be the velocity gradient, there will be the shear stress acting on that. Viscous effect will come to pictures.
Detailed Explanation
Bernoulli’s equation assumes that the flow is frictionless. However, near solid surfaces, friction and shear stress come into play, which complicates how fluids move. This means if a fluid is flowing close to a pipe wall or any surface, Bernoulli's equation cannot accurately describe the flow due to these effects.
Examples & Analogies
Consider sliding a book across a table. The more surface area in contact (like fluid near a wall), the harder it is to slide due to friction. If you tried to calculate the motion of the book using an equation that doesn't account for friction, your results would be inaccurate. Similarly, Bernoulli’s equation needs to account for such friction in real-world fluid situations.
Practical Applications and Limitations
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
That is the reasons Bernoulli equations has a lot of advantages.
Detailed Explanation
Despite its limitations, Bernoulli's equation has significant advantages in simplifying fluid flow analysis. It can easily account for energy losses or gains in different systems, making it versatile for engineers in various applications like piping systems, aerodynamics, and hydraulics.
Examples & Analogies
Think about how engineers design roller coasters. They use concepts like Bernoulli's equation to predict how fast cars will go down slopes and how high they will climb safely. Understanding energy dynamics helps ensure thrilling but safe rides, showcasing the practical advantages of applying Bernoulli’s equation in transportation engineering.
Key Concepts
-
Streamlines: Lines representing fluid flow direction.
-
Bernoulli's Equation: Describes the relationship between pressure, velocity, and height.
-
Discharge Coefficient (Cd): Adjusts theoretical outcomes to reflect real-world inefficiencies.
Examples & Applications
An open tank with fluid flowing out of a nozzle can be analyzed using Bernoulli’s equation to find the outlet velocity based on fluid height.
In wind tunnel testing, Bernoulli's principle can be used to determine lift generated by airfoils by measuring pressure changes.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Pressure, velocity, height in play, Bernoulli's helps us find the way.
Stories
Imagine a river where the water flows fast; the surface is calm, but deep waters have the blast. Using Bernoulli, we can tell, how fast the water’s doing well!
Memory Tools
Remember: PE + KE + Pressure = Constant (PKE = Constant) for Bernoulli's equation.
Acronyms
B.P.E - Bernoulli’s Pressure Energy; helps you remember the components of energy.
Flash Cards
Glossary
- Bernoulli's Equation
A principle in fluid dynamics that relates pressure, velocity, and height in steady, incompressible, frictionless flow.
- Streamline
A line that represents the flow direction of a fluid at every point.
- Coefficient of Discharge (Cd)
A dimensionless number used to characterize the flow efficiency of a nozzle, accounting for energy losses in real applications.
- Flow Energy
The energy associated with the flow of a fluid, quantified by pressure, velocity, and elevation.
Reference links
Supplementary resources to enhance your learning experience.
