Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hydrostatic Pressure
Unlock Audio Lesson
Today we will dive into hydrostatic pressure. Can anyone tell me what hydrostatic pressure is?
Is it the pressure exerted by a fluid at rest?
Exactly! Hydrostatic pressure increases with depth due to the weight of the fluid above. How do you think this impacts the design of wells?
I guess the deeper the well, the higher the pressure at the bottom?
Right! Think of it this way: deeper wells must be structurally sound to withstand this pressure, particularly during seasonal fluctuations in water levels.
Pressure Distribution on Surfaces
Unlock Audio Lesson
Let’s look at pressure distribution. How does pressure behave on a horizontal surface compared to a vertical surface?
On a horizontal surface, the pressure is uniform, right?
Correct! And what about vertical surfaces?
The pressure distribution is trapezoidal since pressure increases with depth?
Exactly! Remember, pressure increases as you go deeper. This knowledge helps in calculating the forces acting on these surfaces.
Calculating Hydrostatic Forces
Unlock Audio Lesson
We can calculate hydrostatic forces by integrating pressure across the area. What do you recall about this process?
We need to know the pressure at the centroid of the area, right?
Exactly! Pressure at the centroid multiplied by the area gives the total force. Can anyone explain why the center of pressure is important?
It's where the resultant hydrostatic force acts, which is crucial for structural design.
Well said! Understanding where the force acts helps in creating safe and effective designs.
Practical Applications and Historical Context
Unlock Audio Lesson
Let’s connect hydrostatics to history. How did ancient engineers utilize these principles in their designs?
Did they design structures that could withstand pressure fluctuations in wells?
That's right! Structures like stepwells have withstood time because of this advanced knowledge of hydrostatics. Can anyone think of modern examples where this knowledge is still relevant?
Bridges and dams, for instance!
Exactly! Hydrostatics is essential for modern engineering just as it was for our ancestors.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explains how hydrostatic pressure acts on submerged surfaces, including vertical, horizontal, and inclined planes. It outlines how ancient stepwells were designed considering these principles and discusses the computation of hydrostatic force and the location of the center of pressure.
Detailed
Basic Principles of Hydrostatic Force
Hydrostatic force refers to the pressure exerted by a fluid at rest. This section explores its fundamental principles, especially in the context of ancient well designs, specifically in stepwells. The depth of these wells can exceed 50 meters, and they serve not only for water supply but also as social gathering places.
Key Points:
- Hydrostatic Pressure Dynamics: Water pressure varies with seasons, being higher during rainy seasons and lower in summer. This aspect is crucial in understanding how water levels affect the well’s structure.
- Pressure Distribution: The section illustrates how pressure on different surfaces—horizontal, vertical, and inclined—changes depending on the water height. A uniform pressure acts on horizontal surfaces, while trapezoidal distributions occur on vertical surfaces.
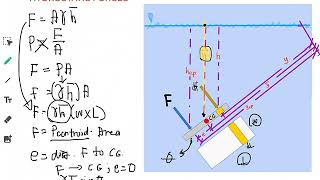
- Calculating Hydrostatic Forces: The force can be determined by integrating the pressure over the submerged area. The center of pressure, where this force acts, is typically below the centroid of the area due to pressure distribution dynamics.
- Practical Applications: The knowledge of hydrostatics allows for proper design and maintenance of structures like wells that have existed for centuries without damage.
Understanding these principles is essential for engineers, architects, and anyone involved in designing structures influenced by fluid dynamics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Hydrostatic Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So if you look at these constructions, they have considered hydrostatic pressure when conditions are extreme, like when a well is full. Simplifying the geometry involves considering surfaces like inclined, vertical, and horizontal surfaces. Water levels fluctuate with seasonal changes — rising during rainy seasons and lowering in summer.
Detailed Explanation
Hydrostatic pressure is the pressure exerted by a fluid at rest due to the force of gravity. In structures like wells, engineers must consider how this pressure varies with depth and how it affects different surfaces. For instance, during extreme conditions, the water pressure can act significantly on inclined, vertical, and horizontal surfaces. It is essential to realize that these pressures change with the water depth; thus, the design must accommodate varying pressure conditions throughout the year.
Examples & Analogies
Imagine a swimming pool. When the pool is full of water, the pressure at the bottom is much greater than at the surface due to the weight of the water above. Similarly, within a well, the pressure increases with depth, requiring architects to design walls that can withstand this pressure.
Pressure Distribution on Surfaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
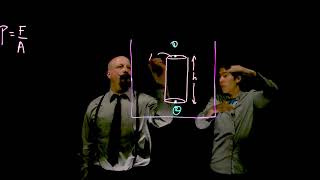
When considering a horizontal surface, the pressure distribution is uniform. The maximum force acts at the centroid of the surface because of uniform pressure. Vertical surfaces experience a trapezoidal pressure distribution, with pressure increasing with depth. An inclined surface also has a trapezoidal distribution as the pressure acts normal to it.
Detailed Explanation
In hydrostatics, the distribution of pressure on surfaces varies depending on their orientation. A horizontal surface experiences uniform pressure, which means that the force is evenly distributed across it, peaking at the center. For vertical surfaces, pressure increases with depth, creating a trapezoidal distribution — the deeper you go, the greater the pressure. For inclined surfaces, the pressure also increases but combines aspects of both horizontal and vertical distributions. This knowledge is vital for calculating the total force acting on these surfaces.
Examples & Analogies
Think of a large sheet of ice on a lake. As you move deeper into the water, the pressure from the water above increases. If you were to visualize the pressure on the ice from each water layer, it starts evenly at the surface but becomes heavier at the bottom, just like the pressure on a vertical dam wall.
Calculating Hydrostatic Force
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To find the total hydrostatic force acting on a submerged surface, we can calculate the area of the pressure distribution multiplied by the pressure at the centroid. The overall force can often be calculated more easily without complex integrations if the centroid is known.
Detailed Explanation
The total hydrostatic force acting on a submerged surface can be computed by taking the pressure at the centroid of the surface and multiplying it by the area of the surface. This is a simplified approach, especially when dealing with uniform fluids. For complex geometries or fluid interactions, integrations might be necessary. Knowing where the centroid lies simplifies calculations, allowing us to avoid complex integral calculus in many cases.
Examples & Analogies
Picture a classroom filled with students sitting at their desks. If you wanted to calculate the total weight pressing down on the floor beneath their desks, you could take the average weight of a student multiplied by the total number of students. Similarly, for submerged surfaces, finding the average pressure at a central point allows us to determine the overall force without needing to average every single point.
Center of Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The center of pressure is where the total hydrostatic force acts. This is not the same as the centroid; it's typically below it for submerged surfaces, as pressure varies with depth.
Detailed Explanation
The center of pressure is crucial in engineering, as it determines how forces applied to a submerged surface behave. It is statistically proven to be below the centroid because the pressure increases with depth. When designing structures like dams or bulkheads, knowing the exact point where the resultant force acts helps in creating stable designs that can withstand various pressures without failing.
Examples & Analogies
Imagine holding a heavy book in one hand. If you can find the 'sweet spot' where the weight feels balanced, that's similar to finding the center of pressure. However, if you held the book higher or lower, it might feel different because of the shifting balance — just like how pressure changes at different depths under the water.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydrostatic Pressure: Pressure that varies with fluid depth.
-
Center of Pressure: The location where total force acts, usually below the centroid.
-
Pressure Distribution: Different shapes exhibit unique pressure distributions based on the geometry.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A vertical dam experiences different pressures at various depths, requiring careful calculations for structural integrity.
-
An ancient stepwell shows the design considerations necessary to manage seasonal water level changes.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Hydrostatic pressure goes down, as the water's weight wears the crown.
📖 Fascinating Stories
-
Imagine a deep well. Each season, the water level rises and falls, pressurizing the walls differently, reminding us of nature's great balance.
🧠 Other Memory Gems
-
C.H.P.: Centroid Height Pressure - remember the centroid for hydrostatic calculations.
🎯 Super Acronyms
P.E.A.C.E.
- Pressure
- Elevation
- Area
- Center of pressure
- and Engineering - think of what aspects matter.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatic Pressure
Definition:
The pressure exerted by a fluid at rest, increasing with depth.
-
Term: Center of Pressure
Definition:
The point where the total hydrostatic force acts on a submerged surface.
-
Term: Trapezoidal Distribution
Definition:
A pressure distribution that varies linearly with depth; typically seen on vertical surfaces.
-
Term: Centroid
Definition:
The center point of a shape or area; used to calculate pressure at that point.