Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hydrostatic Pressure
Unlock Audio Lesson
Today, we're going to explore hydrostatic pressure and how it affects structures like wells. Who can tell me what hydrostatic pressure is?
Is it the pressure exerted by a fluid at rest due to the weight of the fluid above?
Exactly! Hydrostatic pressure increases with depth. The formula is P = P_atmosphere + ρgh. Here, ρ is the fluid density and g is gravity. Can anyone tell me what this means for a well?
So if a well has water increasing in depth, the pressure at the bottom will be much greater than at the top, right?
Right again! Understanding this concept helps us design safer and more effective wells. Remember, greater depth means greater pressure. Let's summarize: Hydrostatic pressure increases with depth!
Pressure Distribution on Different Surfaces
Unlock Audio Lesson
Now, let's talk about how pressure varies based on the surface orientation. What happens on a horizontal surface?
The pressure is uniform across the entire area.
Correct! For vertical surfaces, however, the pressure creates a trapezoidal distribution. Can someone explain why?
It's because pressure increases linearly with depth, so it's higher at the bottom compared to the top.
Exactly! And this is crucial for calculating forces acting on structures. Lastly, for inclined surfaces, what do we do?
We integrate the pressure over the area to find the total force.
Spot on! Remembering these distribution types is essential. Let's summarize: Horizontal surfaces have uniform pressure, vertical surfaces have trapezoidal pressure distribution, and inclined surfaces require integration!
Calculating Center of Pressure
Unlock Audio Lesson
Next, let's determine where the total hydrostatic force acts. This is known as the center of pressure. Why do you think this is important?
I guess it helps in knowing how the structure will behave under load.
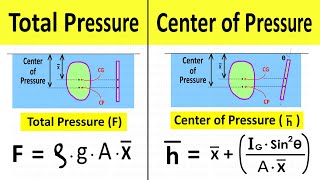
Exactly! The center of pressure is always below the centroid of the area. Given that, what happens to the amount of pressure distributed?
It means that as the pressure increases with depth, the force will shift downwards, influencing design decisions.
Correct again! Always remember: center of pressure informs structural safety and integrity. Let's summarize: The center of pressure is below the centroid and it's crucial for design.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses how ancient wells were designed with consideration for hydrostatic pressure, varying water levels, and how these factors affect forces on different surfaces. Key concepts include pressure distributions on vertical, horizontal, and inclined surfaces, and the significance of calculating the center of pressure in engineering design.
Detailed
Center of Pressure in Structural Design
In structural engineering, understanding the concept of center of pressure is crucial for designing structures that withstand hydrostatic pressure effectively. This section begins by highlighting the historical significance of wells, particularly in areas prone to seasonal changes in water levels. It describes the various kinds of surfaces—horizontal, vertical, and inclined—that are subjected to hydrostatic pressure, emphasizing that pressure varies locally based on depth.
Hydrostatic Pressure Dynamics
The text explains that the pressure at any depth in a fluid is determined by the equation: P = P_atmosphere + ρgh, where ρ is the fluid density, g is the acceleration due to gravity, and h is the depth below the surface. The pressure distribution at horizontal surfaces is uniform and concentrated at the surface's centroid, while for vertical surfaces, pressure increases linearly, resulting in a trapezoidal distribution.
Furthermore, for inclined surfaces, similar principles apply, but the calculations involve integrating pressure areas to derive total force and location of the center of pressure (CP). Understanding these distributions is critical to ensuring structures, particularly ancient well designs, remain functional and safe despite changing hydrostatic conditions.
Lastly, the section touches on derivations for calculating the total force on submerged surfaces and emphasizes practical approaches, including straightforward methods for single liquid cases alongside integration methods for more complex multi-liquid scenarios. The calculation of the center of pressure relative to the surface area informs design decisions crucially related to safety and structural integrity.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Hydrostatic Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Very interestingly when design it that means we need to determine what is the pressure force acting on vertical surface, horizontal surface, and the inclined surface. For a horizontal surface like what here it is a very easy. If I have the fluid and height is h pressure at this point is P atmosphere you know it the pressure at this point will be the P atmosphere plus rho g h. The pressure distributions will be the uniform as it is the horizontal surface.
Detailed Explanation
This chunk introduces the concept of hydrostatic pressure as it relates to different types of surfaces (horizontal, vertical, and inclined) in engineering design. It explains that when designing structures that interact with fluids, engineers must account for the pressure forces acting on these surfaces due to the fluid's weight. Specifically, for horizontal surfaces, the pressure exerted is uniform across the surface, which simplifies calculations. The pressure at a specific depth 'h' is calculated by adding the atmospheric pressure to the pressure resulting from the weight of the fluid above, expressed as 'rho g h'.
Examples & Analogies
Consider a swimming pool. When you are at the bottom of the pool, the water above you exerts pressure downwards. This pressure is the same across the entire bottom of the pool but increases as you go deeper, which is similar to how the hydrostatic pressure is calculated in engineering for surfaces such as dams.
Pressure Distribution on Vertical Surfaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The surface can be a circular, can be elliptical shape, but that what will act on that. So you have the results of that. When you have these vertical surface let we consider this case okay. You can find out that as you know if it is h and this is the h. So the pressure distributions will be the trapezoidal distributions.
Detailed Explanation
This segment explains how the pressure distribution behaves on vertical surfaces when submerged in fluid. It notes that unlike horizontal surfaces, vertical surfaces experience varied pressure across their height, resulting in a trapezoidal distribution of pressure. The pressure is greatest at the bottom of the vertical surface due to the weight of the fluid above it, which is not the case for horizontal surfaces. This difference is crucial for calculating forces on structures that have vertical components, such as walls of water tanks.
Examples & Analogies
Think about the walls of a water tank. The water at the bottom of the tank presses harder against the walls than the water at the top, causing a trapezoidal distribution of pressure. This is similar to the way a person pressing down a pump handle feels more resistance at the bottom of the handle due to the weight of their hand.
Calculating Total Force from Pressure Diagrams
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So we can get the pressure diagram which will be trapezoidal forms and if I know this pressure diagram, I can compute what will be the total force acting due to this pressure diagram which is a very simplified thing to find out the area of these pressure diagrams.
Detailed Explanation
In this section, the focus is on how engineers can calculate the total force acting on a submerged surface based on its pressure diagram. By recognizing that the pressure distribution can be represented as a trapezoid, engineers can simplify their calculations. The total force is determined by calculating the area under the pressure distribution curve, which demonstrates how much force is acting on that specific surface due to the fluid pressure.
Examples & Analogies
Imagine trying to calculate how much someone is pushing against a wall by visualizing the wall covered in sticky notes. Each sticky note represents a different amount of pressure - the more notes there are at the bottom (where the pressure is highest) forms a larger area. By counting the total area covered by sticky notes, you would find out how much total force is being applied against the wall.
Center of Pressure (CP) Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look it that, let us coming to the derivations of the hydrostatic pressures on a submerged surface. That means surface is submerged in a liquid. So we have the atmospheric pressure acting on that. We have the free surface and I am just putting a surface which is the x and y projections in these directions.
Detailed Explanation
This chunk dives into the concept of the center of pressure (CP), which is crucial for understanding where the total hydrostatic force acts on a submerged surface. The center of pressure is calculated by taking into account the pressure distribution across the surface and its depth underwater. As pressure varies with depth, the center of pressure usually lies below the centroid of the area due to increased force from greater depths. This insight is necessary for accurate structural design, especially in hydraulic applications.
Examples & Analogies
Picture a large billboard covered in water with someone trying to push it over from above. While the center of gravity (CG) of the board is easy to find halfway up, the actual point where the water pressure acts to push it is lower than the CG. Just like that billboard, engineers must remember that the point of pressure action is further down, helping stabilize the structure as water levels change.
Integration for Exact CP Location
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look it that, that means to get a total hydrostatic pressure we have to do integrations, the area integration, surface integrations of this quantity okay. If h is the depth, we know it. The depth is a functions with the unit weight. Substituting that any point the pressure will come it as pressure atmospheric pressure plus unit weight of the waters or any liquid what we are considering.
Detailed Explanation
In this part, the concept of mathematical integration is introduced for calculating total hydrostatic pressure accurately. By integrating the pressure over the submerged surface area, engineers can account for variations in pressure across the entire surface. The integration allows for precise determination of both the total force and the specific point of force application (CP), which is critical in structural design involving fluids.
Examples & Analogies
Think of pouring sand into an hourglass. As you pour, the sand settles unevenly and piles up at the bottom; each layer of sand represents a different pressure acting on the glass. To measure how much force is pressing down on the glass, you would not just measure the bottom layer, but account for all the layers above it. In engineering, integration serves the same purpose—it provides a complete picture of the pressure acting on a submerged surface.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydrostatic Pressure: Increases with depth in a fluid.
-
Pressure Distribution: Varies for horizontal, vertical, and inclined surfaces.
-
Center of Pressure: The point of action for the total hydrostatic force, always below the centroid.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
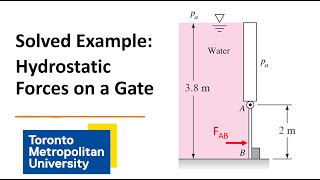
Consider a tank filled with water. The pressure at the bottom can be calculated using the formula P = P_atmosphere + ρgh, where g is gravity.
-
If a submerged vertical plate is 5 m deep in water, its top experiences a pressure of 50 kPa, while the bottom experiences 100 kPa, demonstrating trapezoidal distribution.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Pressure grows deeper, strong and mighty, keeps our wells sturdy and tighty.
📖 Fascinating Stories
-
Imagine an ancient well during a rainy day. As water fills it high, pressure increases, pushing down, reminding builders to calculate wisely for strong structures.
🧠 Other Memory Gems
-
HPC - Hydrostatic Pressure Calculation: Height, Pressure, Centroid.
🎯 Super Acronyms
CP - Center of Pressure
- It's the C-point where the P-force directs.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatic Pressure
Definition:
Pressure exerted by a fluid at rest due to the weight of the fluid above.
-
Term: Center of Pressure (CP)
Definition:
The point where the total hydrostatic force acts on a submerged surface.
-
Term: Trapezoidal Pressure Distribution
Definition:
Pressure distribution pattern that occurs on vertical surfaces, increasing linearly from top to bottom.
-
Term: Surface Integrations
Definition:
Mathematical integration used to calculate forces on submerged surfaces based on pressure distribution.