Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Hydrostatic Pressure Basics
Unlock Audio Lesson
Good day class! Today, we will explore hydrostatic pressure and how it affects the structures of ancient wells. Can anyone tell me what hydrostatic pressure is?
Isn’t that the pressure exerted by a fluid at rest?
Exactly! It's the pressure exerted by water at a specific depth, which increases with depth. We measure it in terms of fluid density, the acceleration due to gravity, and the height of the fluid column.
How do these factors affect the shape of the wells?
Great question! The design considers pressure distributions across different surfaces—horizontal, vertical, and inclined. Each surface type has a different pressure acting on it.
Can we use an acronym to remember these surface types?
Yes! Think of 'HVI': Horizontal, Vertical, Inclined. Remembering 'HVI' can help you categorize the surfaces!
Got it! HVI for Hydrostatic Pressure distributions.
Exactly! Let's summarize the key takeaways from this discussion: Hydrostatic pressure increases with depth, and the design of well structures considers these different pressure distributions.
Calculating Hydrostatic Force
Unlock Audio Lesson
Now that we understand the basic principles, let's talk about calculating hydrostatic forces. How do you think we can determine the force on a submerged surface?
We could integrate the pressure over that surface area?
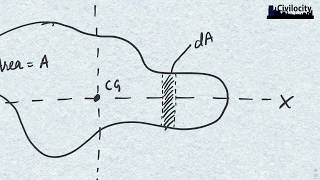
Exactly! By integrating pressure multiplied by area, we find the total hydrostatic force. What happens to pressure at a horizontal surface?
The pressure remains uniform, and the force acts at the centroid!
Correct! For vertical surfaces, the pressure varies. Can anyone describe the pressure distribution?
It forms a trapezoidal shape! The pressure increases with depth.
Well done! This trapezoidal distribution requires a specific integration approach. Let’s summarize this: To find total force, integrate pressure over the area and consider the centroid for force location.
Center of Pressure
Unlock Audio Lesson
Moving on to the center of pressure, why do you think it's important?
Maybe because it determines where the total force acts on the structure?
Exactly! It’s crucial for structural integrity. The center of pressure is typically below the centroid. Why could that be?
Because pressure increases with depth, causing more force to act lower down?
Exactly! More pressure means more force, therefore the center of pressure shifts down. Let's recap: The center of pressure is below the centroid due to varying pressure distribution.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on the principles of hydrostatic pressure in wells, describing how pressure varies across horizontal, vertical, and inclined surfaces due to changes in water level. Key concepts include calculating force areas, understanding pressure distribution, and applying these principles to real-world ancient engineering structures.
Detailed
Integration for Total Hydrostatic Force
This section discusses the fundamental principles of hydrostatic pressure in the context of well systems that are over 2000 years old, particularly in the western part of a country where elaborately designed step wells are found. It highlights how these wells account for seasonal fluctuations in water levels with a depth that extends beyond 50 meters, indicating that they serve not just for water access but also for social gatherings.
Key concepts include distinguishing between pressure distributions across different surfaces:
- Horizontal surfaces exhibit uniform pressure distribution where the force acts at the centroid of the surface.
- Vertical surfaces experience trapezoidal pressure distribution, leading to variations in the pressure at different depths due to hydrostatic pressure, calculated as a function of fluid density, gravitational acceleration, and height.
- For inclined surfaces, the pressure distribution is similar but requires integration of pressure over the surface.
The calculation of total hydrostatic force involves integrating the pressure over these surfaces and determining the center of pressure, which is generally located below the center of gravity of the submerged plane due to pressure distribution effects. The section concludes by discussing the implications of these calculations for the design of ancient structures, showcasing historic knowledge of hydrostatic principles.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Hydrostatic Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So how they have designed it, what is the water pressure acting on this surface. Working on these surfaces, surface A, surface B, one is horizontal and the other is vertical, could have inclined and curved surfaces. These water levels fluctuate. During the summer seasons, it goes down. During the rainy season, it goes up and down with seasonal variability.
Detailed Explanation
This chunk sets the foundation by explaining the concept of hydrostatic pressure as it relates to water levels in wells. Hydrostatic pressure refers to the pressure exerted by a fluid at rest. It varies with height; as the water level increases, so does the pressure exerted on surfaces. Therefore, during the rainy season, the water levels rise, increasing the pressure on the submerged surfaces within the well, while during dry seasons, this pressure decreases as the water level drops.
Examples & Analogies
Imagine a tall glass filled with water. When you pour more water into the glass, the pressure at the bottom of the glass increases due to the additional weight of the water above. Similarly, as rain fills a well, the pressure on the well's surfaces increases, akin to more water in the glass.
Understanding Pressure Distribution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a horizontal surface, the pressure at this point will be P atmosphere plus rho g h. The pressure distributions will be uniform. As it is a horizontal surface, you will have a pressure distribution that will be uniform and the maximum force will act at the centroid of this surface.
Detailed Explanation
This chunk explains how pressure is distributed across different types of surfaces. For horizontal surfaces, pressure increases uniformly with depth due to the hydrostatic pressure equation P = P_atmosphere + ρgh, where ρ is the fluid density, g is the acceleration due to gravity, and h is the depth. This means the deepest point of the surface has the highest pressure, and thus the greatest force acts at the centroid of the surface area.
Examples & Analogies
Think of a sponge submerged in water. The deeper parts of the sponge experience more pressure from the water above. In essence, just like the sponge, surfaces submerged in water experience varying pressure depending on their depth, with the maximum pressure felt at the deepest point.
Force Calculation on Vertical Surfaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For the vertical surface, as you know if it is h1 and this is the h2. The pressure distributions will be trapezoidal because at this point the pressure will come it as rhoh1 and at this point the pressure will be rhoh2.
Detailed Explanation
In this chunk, we learn about how to calculate forces acting on vertical surfaces. The pressure does not increase uniformly across a vertical surface; it increases with depth, leading to a trapezoidal pressure distribution. The pressure at different depths results in different force calculations depending on the height of water above that point, leading to various pressures calculated as rhoh1 and rhoh2.
Examples & Analogies
Consider a dam wall. Water pressure is higher at the bottom where the water is deepest compared to the top. This pressure differential creates a trapezoidal distribution across the dam, which engineers must account for when designing the structure to ensure it can withstand the forces on it.
Center of Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The locations of this force acting is the center of pressure. The center of pressures can be computed it very easily. When you have an inclined surface, we can determine the pressure diagrams.
Detailed Explanation
This part introduces the center of pressure, the point at which the total hydrostatic force can be considered to act. For all surfaces, including inclined surfaces, this calculation is crucial for understanding how forces act on structures submerged in fluids. The center of pressure is usually found below the centroid of submerged surfaces due to how pressure increases with depth.
Examples & Analogies
Think of an umbrella in the rain. The force of water hitting the umbrella is spread out, but if you imagine a single point where all that force is concentrated, that’s like finding the center of pressure. Structurally speaking, knowing where this point is helps engineers determine the best way to design the umbrella to prevent it from breaking or flipping over.
Integration of Hydrostatic Force
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Total force caused by retaining liquid is what we are looking at where it acts. To get a total hydrostatic pressure, we have to do integrations, the area integration, surface integrations of this quantity.
Detailed Explanation
In this chunk, the process of calculating total hydrostatic pressure is discussed. Integration is used to account for the varying pressures across the surface area. By integrating the pressure over the submerged surface, we can find the total force exerted by the fluid. This is crucial in many engineering designs, allowing for accurate force estimations on submerged structures.
Examples & Analogies
Imagine pouring a steady stream of water over a surface. The water doesn’t exert the same force at every point; instead, it varies based on how deep the water is at different points. Integrating is like measuring the cumulative effect of that varying force over the whole surface, ensuring that we accurately understand how the entire surface is affected.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydrostatic pressure increases with depth, leading to a variation in pressure across surfaces.
-
For horizontal surfaces, the pressure distribution is uniform, while vertical surfaces exhibit trapezoidal pressure distribution.
-
The center of pressure generally lies below the centroid of submerged surfaces due to depth-related pressure effects.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A well designed for seasonal water levels must consider how the pressure differs between summer and rainy seasons.
-
In a trapezoidal pressure distribution acting on a vertical wall, calculations can reveal how much force is exerted at different depths.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a well that’s deep, pressure takes a leap, HVI will help you keep, hydrostatic forces neat and cheap.
📖 Fascinating Stories
-
Once upon a time, in a land of deep wells, the wise engineers used measurement spells. They learned pressure rose with depth, shaping their designs with finesse and adept.
🧠 Other Memory Gems
-
To remember the surface types: H for Horizontal, V for Vertical, I for Inclined. 'HVI' keeps them aligned.
🎯 Super Acronyms
Use 'PFD' - Pressure Force Distribution, to remember how pressure affects force on different surfaces.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatic Pressure
Definition:
The pressure exerted by a fluid at rest, increasing with depth.
-
Term: Centroid
Definition:
The center point of a shape where forces can be considered to act.
-
Term: Trapezoidal Distribution
Definition:
A type of pressure distribution that varies linearly across a surface.
-
Term: Integration
Definition:
A mathematical process to find total quantities from a rate of change.