Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hydrostatic Pressure
Unlock Audio Lesson
Today, we're discussing hydrostatic pressure, which is the pressure exerted by a fluid at rest. Can anyone tell me why this pressure changes with depth?
I think it’s because the deeper you go, the more fluid there is above you!
Exactly! The pressure at a certain depth is affected by the weight of the fluid above. This leads to a key formula: Pressure = atmospheric pressure + (density × gravity × height). Remember this as PAGh!
What does 'PAGh' mean?
PAGh represents Pressure (P), Atmospheric pressure (A), Gravity (G), and height (h). It's a simple way to recall how pressure varies with depth.
Can we always ignore atmospheric pressure?
Good question! In many cases, especially for deep bodies of water, atmospheric pressure can be negligible compared to hydrostatic pressure. Let's keep this in mind as we discuss surfaces.
What about surfaces? Does pressure act differently on horizontal vs. vertical surfaces?
Yes! Pressure on a horizontal surface is uniform, while on a vertical surface, it varies. We will calculate forces for both types.
In summary, hydrostatic pressure varies with depth due to the weight of the fluid above, and this affects how pressure acts on different surfaces.
Pressure Distribution on Surfaces
Unlock Audio Lesson
Let’s now talk about how pressure acts on different surfaces. On a horizontal surface, the total pressure force acts at the centroid. What happens there?
The pressure is uniform, right?
Yes! On horizontal surfaces, the pressure distribution is constant, which simplifies calculations. Now, what if we moved to vertical surfaces?
It becomes trapezoidal, so the pressure is lower at the top and higher at the bottom.
Correct! This variance means we have to integrate to find the total force. Why is that important?
To get the total effect of the pressure on the structure?
Exactly! Understanding this helps us design safe structures. For instance, total force = average pressure × area.
In summary, pressure on horizontal surfaces is uniform, while vertical surfaces require more complex calculations due to varying pressure distributions.
Determining the Center of Pressure
Unlock Audio Lesson
Now let’s focus on the center of pressure. Does anyone know why this point is important?
Is it where the total force acts?
Yes! The center of pressure is crucial for structural stability. It’s usually below the centroid due to the pressure distribution.
Why is it always below the centroid?
Great question! It’s because the pressure increases with depth, causing the force to shift downwards. Mathematically, we can find it using the formula involving the moment about the centroid.
So how do we calculate it?
We integrate pressure times area to find the location of CP. Remember, it plays a crucial role in designing structures that withstand fluid forces.
In conclusion, the center of pressure is where the resultant force acts, typically situated below the centroid due to varying pressure.
Practical Applications and Examples
Unlock Audio Lesson
Let's look at practical applications. How do you think the concepts we've learned today apply to engineers designing structures like dams or wells?
They need to account for pressure when designing walls to prevent failures.
Exactly! Engineers evaluate forces acting on submerged surfaces to ensure safety. For example, stepwells had aesthetic purposes but were designed effectively using hydrostatic principles.
So, design safety is mainly about understanding where forces act?
Precisely! Knowing the center of pressure helps predict where the force will exert most influence. It’s critical for structural integrity.
In summary, the concepts we’ve explored lay the foundation for effectively designing and evaluating various structures subjected to hydrostatic pressure.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section begins with an overview of ancient well designs, focusing on the impact of hydrostatic pressure on different surfaces of the wells. It details how to determine the pressure force on horizontal, vertical, and inclined surfaces, explains the concept of center of pressure, and delves into how these principles influence structural design.
Detailed
Center of Pressure Determination
This section delves into the concept of hydrostatic pressures acting on submerged surfaces and the determination of the center of pressure (CP). The discussion begins with the historical context of stepwells, emphasizing how ancient structures utilized hydrostatic principles in their design to withstand seasonal water fluctuations.
Key Concepts:
- Hydrostatic Pressure: Pressure exerted by a fluid at rest due to the force of gravity, which varies with depth.
- Surface Types:
- Horizontal Surfaces: Experiences uniform pressure distribution; the total force acts at the centroid.
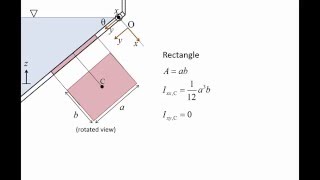
- Vertical Surfaces: Exhibits trapezoidal pressure distribution; requires integration for total force and understanding of its center of pressure.
- Inclined Surfaces: Similar to vertical surfaces but requires adjustments for pressure distribution calculations.
- Total Force Calculation: This is achieved by integrating pressure over the area of interest, resulting in a relationship where total force equals pressure at the centroid multiplied by the area.
- Center of Pressure: Represents the point where the total force acts on a submerged plane and is mathematically lower than the centroid due to pressure distribution characteristics.
The importance of properly calculating these forces lies in their application for designing structures capable of enduring varying hydrostatic pressures and ensuring longevity and functionality.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Hydrostatic Pressure Basics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, if you look at these the constructions how they have considered the hydrostatic pressure when you have a extreme flow conditions or when you have this well are at the full filled conditions. Like for examples this well is considered let be the flood level here. Now, I am not considering so complex geometry what is there. If I consider very simplified geometry what I had sketching it here these are there are inclined surface, there are vertical surface, there are may be curved surface are there and there are horizontal surface and all. And these water levels if you can understand it fluctuates okay. During the summer seasons it goes down. During the rainy season it goes up. So it goes up and down with a seasonal variability.
Detailed Explanation
Hydrostatic pressure is the pressure exerted by a fluid at equilibrium due to the force of gravity. In the context of wells, this pressure changes with the water level, which fluctuates seasonally. During rainy seasons, the well is filled to a higher level, increasing the hydrostatic pressure on the surfaces in contact with the water. In summer, the level decreases, reducing the pressure. Understanding this concept helps in assessing how structures like wells are designed to handle varying pressures.
Examples & Analogies
Think of a balloon filled with water. When you squeeze it, the water (representing the hydrostatic pressure) pushes back against your hand. Similarly, in a well, when it fills up during the rainy season, it’s like the balloon being filled: the pressure increases on the walls of the well.
Pressure on Different Surfaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
And how they have designed it. What is the water pressure is acting on this surface, working on these surface it is surface A, surface B, one is a horizontal, another is vertical, another is inclined and it could you have the curve nature what is there? There are the curve, the projections and all. How much of water pressure acted when you have totally the tank while well is in a filled condition. Very interestingly when design it that means we need to determine what is the pressure force acting on vertical surface, horizontal surface, and the inclined surface.
Detailed Explanation
When determining how pressure affects various surfaces, it's essential to analyze each surface type: horizontal, vertical, and inclined. For horizontal surfaces, pressure is uniform across its area. For vertical surfaces, pressure increases with depth, leading to a trapezoidal pressure distribution. Inclined surfaces present even more complexity but generally follow the same principles: pressure is highest at the bottom and decreases above.
Examples & Analogies
Imagine a rectangular pool. The pressure at the bottom because of the water is much greater than just a few inches down the side. But if you were to look at the side of the pool, you would see that pressure is not the same all the way up.
Calculating Pressure Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So we can get the pressure diagram which will be trapezoidal forms and if I know this pressure diagram, I can compute what will be the total force acting due to this pressure diagram which is a very simplified thing to find out the area of these pressure diagrams, okay multiplied with the perpendicular distance or that what is many of the time we consider unit distance.
Detailed Explanation
To calculate the total force due to pressure on a submerged surface, one can graph the pressure distribution, which often appears as a trapezoidal shape for vertical surfaces. The area under this graph represents the total force, which can be calculated by multiplying the area by the distance from the water surface to the centroid of that area.
Examples & Analogies
Think about pricing at a store: if a product costs more the deeper you get into the store, then at any given moment, you can consider the total amount spent as the 'pressure'. The deeper you are in the store, the more you’re paying. When you chart out your expenses, you might find the total amount you would spend based on where you're standing, similar to calculating pressure on a submerged surface.
Center of Pressure Concept
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us compute to that we need to compute center of pressure. That means, the point of action of total hydrostatic force on this submerged surface. That what I tried to explain it that it is not that where his force acting. That is what also the plays a major role to design a structures okay, design a gate, design a any wall we need to know it where this force, the location of the force also matter it and that is what the center of pressures.
Detailed Explanation
The center of pressure is the point where the total hydrostatic force can be considered to act on a surface. It is essential for designing structures, as knowing this point helps engineers determine how to balance forces more effectively and ensure structural stability.
Examples & Analogies
Imagine balancing a seesaw. The point where you sit to balance your side acts like the center of pressure. If you sit too far to one side, the seesaw tips over. Understanding where forces act helps engineers design balanced and stable structures.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydrostatic Pressure: Pressure exerted by a fluid at rest due to the force of gravity, which varies with depth.
-
Surface Types:
-
Horizontal Surfaces: Experiences uniform pressure distribution; the total force acts at the centroid.
-
Vertical Surfaces: Exhibits trapezoidal pressure distribution; requires integration for total force and understanding of its center of pressure.
-
Inclined Surfaces: Similar to vertical surfaces but requires adjustments for pressure distribution calculations.
-
Total Force Calculation: This is achieved by integrating pressure over the area of interest, resulting in a relationship where total force equals pressure at the centroid multiplied by the area.
-
Center of Pressure: Represents the point where the total force acts on a submerged plane and is mathematically lower than the centroid due to pressure distribution characteristics.
-
The importance of properly calculating these forces lies in their application for designing structures capable of enduring varying hydrostatic pressures and ensuring longevity and functionality.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of calculating hydrostatic pressure on a submerged wall using known parameters.
-
Case of a well designed using hydrostatic principles to illustrate how ancient engineers used these concepts.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Pressure goes deep, like roots of a tree; as water flows down, it affects me!
📖 Fascinating Stories
-
Imagine a castle built by ancient engineers. They understood that water pushes down, so they built thick walls below and made them fancy to welcome the cool water and friends.
🧠 Other Memory Gems
-
Remember PAGh for hydrostatic pressure calculation: P for pressure, A for atmospheric pressure, G for gravity, and h for height!
🎯 Super Acronyms
CP stands for Center of Pressure, where the total force feels its greatest impact on a submerged body.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatic Pressure
Definition:
The pressure exerted by a fluid at rest due to the weight of the fluid above a given point.
-
Term: Center of Pressure (CP)
Definition:
The point at which the total pressure force acts on a submerged surface, typically located below the centroid.
-
Term: Hydrostatic Force
Definition:
The total force exerted by a fluid at a submerged surface due to hydrostatic pressure.