Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hydrostatic Pressure
Unlock Audio Lesson
Today we'll dive into hydrostatic pressure. Can anyone tell me what hydrostatic pressure is?
Isn’t it the pressure exerted by a fluid at rest?
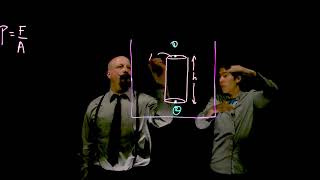
Exactly! Hydrostatic pressure increases with depth and can be described by the formula P = P_atmos + ρgh. Remember, ρ is the fluid density and h is the depth!
So deeper water creates more pressure?
Yes! As we go deeper, h increases. That’s essential to remember - *Deeper = More Pressure*.
Is the atmospheric pressure also part of that?
Yes! But often we focus on the pressure due to the fluid itself when calculating forces.
What if the fluid has different densities?
Good question! If different liquids are involved, we may need to use integration to solve the pressures correctly.
To remember the pressure formula, think of it as 'Pressure equals Atmosphere plus weight of depth'. Let's move on to pressure distribution!
Pressure Distribution on Surfaces
Unlock Audio Lesson
Next, let’s discuss how pressure acts differently on horizontal vs. vertical surfaces. Can someone explain what happens in these cases?
Horizontal surfaces experience uniform pressure, right?
Correct! And what about vertical surfaces?
I think they have trapezoidal pressure distributions because the pressure increases with depth.
Exactly! As we move down a vertical surface, the pressure increases, creating a trapezoidal shape for the pressure diagram.
How do we calculate the total force from those pressure distributions?
We calculate the total force by integrating the area of the pressure distribution and multiplying it by the pressure at the centroid. Remember, force = Area x Pressure at Centroid.
So, if we get the area and know where the centroid is, we can find the total force!
Exactly! Visualize this with our *Area and Centroid* laminated chart. Now onto computing the center of pressure!
Center of Pressure
Unlock Audio Lesson
Who can explain what the center of pressure is?
Is it the point where the total force acts on a submerged surface?
Correct! It’s essential to know where this point is to ensure proper design. Typically, the center of pressure is below the centroid, due to pressure distribution.
How do we calculate its position?
We can calculate it using the moments about an axis, similar to solid mechanics principles. Integrating will yield the exact position.
How does this affect the design of structures?
Great question! Knowing the center of pressure helps engineers design safer and more stable structures that can withstand the forces acting on them during different conditions.
Remember, *CP is below CG*! Practice this concept with your homework and we will discuss it in our next class.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore how hydrostatic pressures vary with depth in liquids and how these variations influence design considerations for submerged surfaces, particularly in historical structures such as stepwells. The derivations of pressure forces acting on horizontal and vertical surfaces, as well as methods to calculate total forces and centers of pressure, are discussed extensively.
Detailed
Detailed Summary
This section elaborates on the principles of hydrostatic pressure, particularly in structures like ancient stepwells, which showcase impressive engineering considering the effects of hydrostatic forces. The passage breaks down how the pressure varies depending on the geometry and depth of submerged surfaces.
- Hydrostatic Pressure Fundamentals: Hydrostatic pressure increases with depth due to the weight of the fluid above. The basic formula is given as:
Pressure (P) = Atmospheric Pressure (P_atmos) + ρgh
where ρ is the density of the fluid, g is the acceleration due to gravity, and h is the height of fluid above that point.
- Pressure Distribution: We discuss how pressure distributions differ based on surface orientation: horizontal surfaces bear uniform pressure, while vertical surfaces experience trapezoidal distributions due to increasing pressure with depth. This section gives insights into calculating forces based on these distributions:
- Total Force = Area of Pressure Distribution x Pressure at Centroid
- Center of Pressure shifts below the geometric center due to distribution characteristics.
- Integration for Complex Shapes: For irregular shapes or multi-liquid scenarios, integration is necessary to accurately determine pressure forces. Relevant equations and methodologies guide the design of structures that can withstand these forces over time.
- Applications and Significance: The knowledge derived from understanding hydrostatic pressures has allowed ancient civilizations to create long-lasting audacious infrastructural designs that remain functional even after centuries. These principles are foundational in engineering applications, notably in dams and aqueducts.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Hydrostatic Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look it that, let us coming to the derivations of the hydrostatic pressures on a submerged surface. That means surface is submerged in a liquid. So we have the atmospheric pressure acting on that. We have the free surface and I am just putting a surface which is the x and y projections in these directions is it look it from this point you will have an inclined surface which is having this x and y.
Detailed Explanation
In this introduction, we are focusing on hydrostatic pressure, which is the pressure exerted on a submerged surface. When a surface is submerged in a liquid, atmospheric pressure affects it, combined with the pressure from the liquid above it. In our scenario, we visualize it with a surface that is inclined, and we need to analyze the force acting on it due to these pressures.
Examples & Analogies
Think of a person diving into a swimming pool. As they go deeper, they feel more pressure on their body from the water above them. The deeper they go, the greater the pressure, similar to how the submerged surfaces experience hydrostatic pressure.
Calculating Forces on Small Elements
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If these two things we know it then we can design these things that what type of material to be used, what type of lifting arrangements will be there, if this is as equal to a get conditions. The submerged plane can be considered as a get conditions. So total force caused by retaining liquid that what we are looking and directions and lineup for actions as the directions will be always perpendicular to the surface that what the directions and the line of actions what of the force is the center of pressure.
Detailed Explanation
To understand how hydrostatic forces act on submerged surfaces, we focus on small elements of the surface area. Each element experiences a force due to the water pressure, which acts perpendicularly to the surface. The total force on the submerged surface can be determined by summing up the contributions from all these small elements. This also helps us understand how to design structures, like gates or walls, that need to resist this force.
Examples & Analogies
Imagine a large sheet of paper being pressed down on by a heavy book. Each small part of the paper experiences a force from the book's weight. In a similar way, each small element of a submerged surface feels the pressure from the water above it.
Integration of Pressure Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I consider a small element okay, let me consider a small element. In this small element of the dA if the pressure is P Then P into dA will be the force, pressure into area will be force.
Detailed Explanation
Here, we are taking a more mathematical approach by introducing integrals. For each small area element (dA) on our submerged surface, the force can be calculated as the pressure (P) multiplied by the area. To find the total force acting on the entire submerged surface, we would integrate these forces across the entire area.
Examples & Analogies
Think of using a sponge to absorb water. Each tiny part of the sponge absorbs a certain amount of water based on the pressure of the water it's in. To find out how much water the entire sponge absorbs, you need to consider all those tiny parts together—just like using integration to find total force.
Force Calculation and Centroid Finding
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
That means if I just put all these values what I am getting this part, which is the Pc multiply the area that what will come is the force.
Detailed Explanation
Once we have integrated and found the pressure at the centroid of the submerged surface, we can calculate the total hydrostatic force. This is done by multiplying the pressure at that centroid (Pc) by the area of the submerged surface. This gives us a clear numerical value for the force acting on that surface.
Examples & Analogies
Picture a water balloon. When you press on it, the pressure at the center of the balloon will tell you how much force you're exerting. Just like that, knowing the pressure at the centroid of an area lets us calculate the total force acting on it.
Understanding the Center of Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us compute to that we need to compute center of pressure. That means, the point of action of total hydrostatic force on this submerged surface.
Detailed Explanation
In the analysis of hydrostatic forces, understanding where this total force acts is crucial. This point is known as the center of pressure. It is determined by considering the moments produced by the force about a reference point (like an axis) and can be calculated using principles similar to those used in solid mechanics.
Examples & Analogies
If you think of a seesaw, the point where the forces are balanced is like the center of pressure. Just as the seesaw tilts towards the heavier side, the center of pressure helps us understand how the structure will behave under hydrostatic forces.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydrostatic Pressure: Increases with depth and is given by the formula P = P_atmos + ρgh.
-
Pressure Distribution: Varies on horizontal (uniform) and vertical (trapezoidal) surfaces.
-
Center of Pressure: Always located below the centroid due to pressure distribution characteristics.
-
Integration Techniques: Utilized to calculate forces and pressure effects on complex geometries.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of calculating the pressure at a depth of 10m in water: P = P_atmos + ρgh.
-
Illustration of how pressure acts differently on a submerged rectangular vs circular surface.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Hydrostatic might seem grand, / But pressure builds on sand; / With depth you will find, / More weight from behind.
📖 Fascinating Stories
-
Imagine diving into a pool. The deeper you go, you feel pressure on your ears—this is hydrostatic pressure acting upon you.
🧠 Other Memory Gems
-
Remember 'P for Pressure, A for Area, C for Center' to link pressure force calculation.
🎯 Super Acronyms
HAP = Hydrostatic, Area, Pressure - key terms to remember.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatic Pressure
Definition:
The pressure exerted by a fluid at rest, increasing with depth.
-
Term: Centroid
Definition:
The geometrical center of an area, where total area can be thought to act.
-
Term: Center of Pressure
Definition:
The point at which the total hydrostatic force acts on a submerged surface.
-
Term: Pressure Distribution
Definition:
The variation of pressure across a surface, which differs based on orientation.