Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Hydrostatic Pressure
Unlock Audio Lesson
Today, we're diving into hydrostatic pressure, especially how it affects constructions like wells. Can anyone tell me why understanding water pressure is crucial for engineers?
It's important because it helps in designing structures that can withstand the forces of water.
Exactly! Hydrostatic pressure plays a vital role in ensuring that structures remain stable, especially when water levels fluctuate. Remember, as water depth increases, so does pressure—this is key.
What about different surface orientations? Do they affect pressure too?
Great question! The pressure is distributed differently on horizontal, vertical, and inclined surfaces. Let's explore these differences.
Pressure Distribution on Different Surfaces
Unlock Audio Lesson
So, how does pressure behave on a horizontal surface?
It should be uniform since the pressure acts straight down due to gravity.
Correct! And for vertical surfaces, what happens?
The pressure increases with depth, forming a trapezoidal distribution.
Right again! This means as you go lower, the pressure contributing to forces exerted on the surface increases, leading to potential structural issues if not designed properly.
Calculating Total Hydrostatic Force
Unlock Audio Lesson
Let’s talk about how we calculate the total hydrostatic force on a submerged surface. Can someone explain the basics?
We consider the pressure at the centroid of the area and multiply it by the area to find the force?
Yes! So we can simplify our calculations by finding pressure at the center of gravity. Does anyone remember how that pressure is computed?
It’s the atmospheric pressure plus the water pressure based on depth.
Exactly! This equation is crucial for ensuring that we accurately estimate the forces acting on our structures.
Center of Pressure and Its Importance
Unlock Audio Lesson
Now, let's consider the center of pressure. How does it differ from the center of gravity?
The center of pressure is always below the center of gravity for submerged surfaces, right?
That's right! This positioning is critical as it ensures stability against the forces acting on the structure. Can anyone think of examples where this might be particularly important?
Maybe in dam structures or large underwater barrier systems?
Great thinking! Understanding where that force acts helps engineers design safer and more efficient structures.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section provides an overview of how hydrostatic pressure is calculated in submerged surfaces, the importance of understanding water pressure distribution on different surfaces of wells, and how ancient designs effectively incorporate these principles. It examines horizontal, vertical, and inclined surfaces and explains how to determine the total force and center of pressure.
Detailed
Hydrostatic Pressure Considerations
This section explores the concepts associated with hydrostatic pressure, particularly in the context of ancient well constructions.
Ancient wells, some of which are over 2000 years old, serve not only as sources of water but also as spaces for social gatherings. These designs showcase remarkable architectural skills, especially in regions where seasonal rainfall significantly alters water levels. This dual purpose of well designs highlights how effectively ancient civilizations utilized hydrostatic principles to ensure structural integrity during various flow conditions.
Key Concepts:
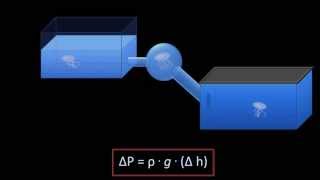
Hydrostatic pressure pertains to the pressure exerted by a fluid at equilibrium due to the force of gravity. The distribution of pressure acting on submerged surfaces varies depending on the orientation of these surfaces:
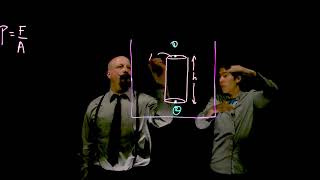
- Horizontal Surfaces: Pressure is uniform, governed by the formula:
P = P_atmosphere + ρgh
where P signifies pressure, ρ signifies fluid density, g is acceleration due to gravity, and h is the height of the fluid above the point of measurement.
- Vertical Surfaces: The pressure distribution follows a trapezoidal shape, as pressure increases with depth.
- Inclined Surfaces: Similar to vertical surfaces, the pressure distribution can be integrated to find the area it occupies, affecting the force felt across the surface.
Understanding these distributions is crucial for calculating the total hydrostatic force acting on these surfaces, along with determining its center of pressure (CP). This principle signifies that CP is always located below the center of gravity (CG) of the submerged surface due to the nature of fluid pressure distribution.
This knowledge aids in designing structures such as gates and walls and ensures they remain functional and safe under various conditions.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Hydrostatic Pressure
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So if you look at these the constructions how they have considered the hydrostatic pressure when you have extreme flow conditions or when you have this well are at the full filled conditions. Like for examples this well is considered let be the flood level here. Now, I am not considering so complex geometry what is there.
Detailed Explanation
In this chunk, we discuss the importance of hydrostatic pressure in the design of wells and structures. Hydrostatic pressure is the pressure exerted by a fluid at rest, due to the force of gravity. It is crucial in ensuring that constructions like wells can withstand varying water levels, especially during floods and dry seasons. The text mentions that we’ll look into simplified geometries to understand these pressures better, avoiding complexities while still capturing the essential ideas.
Examples & Analogies
Imagine a water balloon. When you fill it with water, the pressure inside it increases as more water is added. If the balloon is too weak (like a poorly designed well), it might burst under pressure. Engineers consider these pressures to ensure that structures like water tanks can safely hold the water without collapsing.
Variation of Water Levels
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These water levels fluctuate. Okay. During the summer seasons it goes down. During the rainy season it goes up. So it goes up and down with a seasonal variability.
Detailed Explanation
Water levels in wells change with seasons; they rise during rainy seasons and fall in dry seasons. This variation significantly affects the hydrostatic pressure acting on well surfaces. As water levels change, the pressure increases when the water level is high and decreases when it falls. Understanding these variations is crucial for designing structures that can withstand the pressure changes throughout the year.
Examples & Analogies
Consider a sponge soaking in water. When you first dip it in, it absorbs water and expands. When you take it out, it starts to shrink as it dries. Similarly, wells 'expand' under pressure when filled with water and 'shrink' when empty, which engineers must account for.
Pressure Distribution on Surfaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
How much of water pressure acted when you have totally the tank while well is in a filled condition. Very interestingly when design it that means we need to determine what is the pressure force acting on vertical surface, horizontal surface, and the inclined surface.
Detailed Explanation
In this chunk, we focus on how hydrostatic pressure applies to different surface orientations of the well. There are three main types: horizontal, vertical, and inclined surfaces. The pressure varies based on the orientation of the surface due to the depth of water above it. For example, the pressure is uniform on a horizontal surface but varies linearly on vertical surfaces, creating a trapezoidal distribution of pressure.
Examples & Analogies
Think about how a piece of paper behaves when you blow on it. If you blow directly onto the flat surface (horizontal), the pressure is even (similar to pressure on a flat surface of a well). Now if you angle the paper and blow from above (like a vertical surface), the force of the air creates a different effect depending on your angles, just like how water affects different surfaces of a well.
Hydrostatic Pressure Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The pressure for horizontal surface will be uniform as it is the horizontal surface. As it is a horizontal surface you will have pressure distributions will be uniform.
Detailed Explanation
The pressure on a horizontal surface is uniform, meaning the same pressure acts across the entire area of that surface. This uniform pressure increases with depth according to the formula: P = Patm + ρgh, where P is the pressure, Patm is atmospheric pressure, ρ is the density of the fluid, g is the acceleration due to gravity, and h is the height of the fluid above the point.
Examples & Analogies
Picture the bottom of a swimming pool. When you dive to the bottom, the pressure on your ears increases uniformly; it doesn't matter where you are in the pool but only how deep you are. This is similar to how pressure is distributed across the horizontal bottom of a well.
Analyzing Vertical and Inclined Surfaces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For a vertical surface, the pressure diagrams will be trapezoidal because the pressure varies with depth. As you know if it is h and this is the h1 and h2.
Detailed Explanation
Vertical surfaces experience varying pressure, leading to a trapezoidal pressure distribution. This is because the deeper the water, the more pressure it exerts on the surface area below it. The pressure increases linearly with depth, causing the trapezoidal shape when plotted. This understanding is critical for engineers to calculate the total force acting on the structure accurately.
Examples & Analogies
Consider a sandwich with layers of different ingredients. As you press down the top layer, the pressure isn’t the same through the sandwich; it changes as the pressure is exerted through each layer depending on how thick it is. This is like how the pressure changes with depth in water.
Total Hydrostatic Force Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We can compute what will be the total force acting due to this pressure diagram which is a very simplified thing to find out the area of these pressure diagrams.
Detailed Explanation
To find total hydrostatic force acting on a surface, using the area of the pressure distribution diagram is crucial. By calculating the area under the pressure curve and considering the perpendicular distance from where the force acts, engineers can determine the total force effectively. This involves integrative calculations but can also be simplified by knowing the pressure at the centroid of the area.
Examples & Analogies
Think of how a weight is distributed on a large trampoline. The total weight pressing down affects how much the trampoline sags. By calculating the total weight and the area over which it acts, you can predict how deep it will sag. This is similar to how engineers calculate water pressure acting on structures.
Center of Pressure Location
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us compute to that we need to compute the center of pressure, that means, the point of action of total hydrostatic force on this submerged surface.
Detailed Explanation
The center of pressure is crucial as it is the point where the total hydrostatic force effectively acts. It is usually located below the centroid of the surface area due to the increasing pressure with depth. To find it, engineers perform calculations involving the moments of force distributions, helping them design effective structures that can cope with hydrostatic pressures.
Examples & Analogies
Imagine balancing a seesaw. If you put a heavier weight on one side, it will tip towards that side. The center of mass changes based on where the weight is. Similarly, the center of pressure indicates where the total force acts, and it's important for maintaining balance in engineering designs.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Hydrostatic pressure pertains to the pressure exerted by a fluid at equilibrium due to the force of gravity. The distribution of pressure acting on submerged surfaces varies depending on the orientation of these surfaces:
-
Horizontal Surfaces: Pressure is uniform, governed by the formula:
-
P = P_atmosphere + ρgh
-
where P signifies pressure, ρ signifies fluid density, g is acceleration due to gravity, and h is the height of the fluid above the point of measurement.
-
Vertical Surfaces: The pressure distribution follows a trapezoidal shape, as pressure increases with depth.
-
Inclined Surfaces: Similar to vertical surfaces, the pressure distribution can be integrated to find the area it occupies, affecting the force felt across the surface.
-
Understanding these distributions is crucial for calculating the total hydrostatic force acting on these surfaces, along with determining its center of pressure (CP). This principle signifies that CP is always located below the center of gravity (CG) of the submerged surface due to the nature of fluid pressure distribution.
-
This knowledge aids in designing structures such as gates and walls and ensures they remain functional and safe under various conditions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An ancient stepwell in India illustrates creative use of hydrostatic principles to maintain stability and manage seasonal water variation.
-
Pressure calculations in a dam wall show that the forces acting increase with water depth, influencing the design and safety measures implemented.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Deep in the water, pressure will rise, Understanding these forces keeps us wise.
📖 Fascinating Stories
-
Imagine a well full of water, with children around it. Each child represents a different depth, feeling varying pressure as they dive deep or stay shallow, illustrating how depth influences force.
🧠 Other Memory Gems
-
For 'CP', remember: 'C’ is for Center, ‘P’ is for Pressure, think of where all the pressure is centered on submerged walls.
🎯 Super Acronyms
HCP — Hydrostatic Pressure = Change in depth results in Pressure!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hydrostatic Pressure
Definition:
The pressure exerted by a fluid at equilibrium due to the force of gravity.
-
Term: Center of Pressure (CP)
Definition:
The point where the total hydrostatic force acts on a submerged surface.
-
Term: Center of Gravity (CG)
Definition:
The average location of the weight of an object; for submerged surfaces, it is usually above the center of pressure.
-
Term: Pressure Distribution
Definition:
The variation of pressure over a given area, depending on the type of surface and orientation.
-
Term: Trapezoidal Distribution
Definition:
A pressure distribution that increased with depth, typically observed in vertical surfaces submerged in fluid.