Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Dimensional Homogeneity
Unlock Audio Lesson
Welcome students! Today we are diving deep into dimensional analysis, specifically focusing on Buckingham's Pi Theorem. Can someone explain why we care about dimensional homogeneity in experiments?
It helps ensure that the equations we're using make sense, right? Like the dimensions on both sides of an equation need to match?
Exactly! If we have an equation, the left-hand side must have the same dimensions as the right-hand side. This principle keeps our calculations valid.
So, how does this relate to complex experiments?
Great question! By ensuring dimensional homogeneity, we can identify which variables are critical, making our experiments more efficient. Let's think about a specific example to clarify this.
Understanding Buckingham's Pi Theorem
Unlock Audio Lesson
Now, let’s discuss Buckingham's Pi Theorem itself. Can anyone summarize what it states?
It states that for a given problem involving n variables, we can form dimensionless groups by reducing variables based on their units.
Well done! More specifically, if we have n variables and k fundamental dimensions, the number of dimensionless groups we can form is given by n - k. It's a powerful tool for simplifying complex problems!
How do we apply this in real-world scenarios?
Let’s take the example of drag force on a sphere in flow. We consider variables like diameter, velocity, and fluid properties. Who can formulate the dimensionless groups using Buckingham's theorem from these parameters?
Application of the Theorem
Unlock Audio Lesson
Using Buckingham's Pi Theorem allows us to create relationships between our variables in fluid mechanics. Let's revisit the drag force on a sphere. What do we need to consider?
The diameter of the sphere, the fluid velocity, and the viscosity, right?
Exactly! This gives us several variables to work with. Now, by reducing these with Buckingham’s Pi process, we can define dimensionless numbers, like the Reynolds number, which characterizes flow regimes.
Does this mean we could reduce the number of experiments we run?
Yes! By understanding the dimensionless relationships, we can reduce the number of experiments significantly, making our research more cost-effective.
Practice and Example Problems
Unlock Audio Lesson
Let’s practice with a problem! Suppose we have a cylinder, and we're looking at drag forces based on various dimensions. How would we identify our dimensionless groups?
We would identify the key parameters and check which fundamental quantities they relate to, like mass and length.
Exactly! We need to see how many independent variables we have. The key is to look for what remains consistent across our variables.
Can you give us a hint on calculating the Reynolds number?
Sure! The Reynolds number is calculated using fluid velocity, characteristic length, and kinematic viscosity. It's quantified as Re = (od * density * velocity) / viscosity.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section covers Buckingham's Pi Theorem, explaining its significance in dimensional analysis and how it assists in deriving dimensionless numbers that simplify the analysis of relations between physical quantities. Examples are provided to illustrate the application of the theorem in fluid mechanics.
Detailed
Detailed Summary
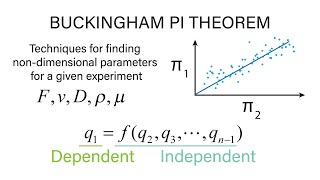
Buckingham's Pi Theorem is a vital concept in the field of fluid mechanics that deals with dimensional analysis. This theorem allows engineers and scientists to create dimensionless parameters, which simplifies the relationship between different physical variables. The core idea is that if you have a set of n physical variables, the number of independent dimensionless groups you can form, also known as Pi terms, is equal to n minus the number of fundamental dimensions involved (mass, length, time).
In practical terms, when designing experiments, especially those related to fluid dynamics, it can be prohibitively expensive to conduct numerous tests with all combinations of variables. Buckingham's Pi Theorem aids in reducing experimental work by highlighting the key dimensionless groups to consider, allowing for fewer experiments while still capturing critical relationships. The chapter discusses the drag force acting on a sphere in fluid motion as a practical application of this theorem.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Buckingham's Pi Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Buckingham's Pi theorem is fundamental for understanding how to analyze and simplify complex physical problems by reducing the number of variables involved.
Detailed Explanation
Buckingham's Pi theorem states that if you have a physical problem with a certain number of variables, you can reduce this problem to a set of dimensionless parameters. This means you take into account the physical dimensions of each variable and group them together to form dimensionless quantities (called Pi terms), which reveal relationships between variables without the clutter caused by units.
For example, if you are studying the drag force experienced by an object in a fluid (like a sphere), you would start by listing all the variables affecting the drag force, such as the diameter of the sphere, fluid velocity, fluid density, and dynamic viscosity. The theorem helps find a simplified equation that can predict how drag varies with these variables without needing to know their specific units.
Examples & Analogies
Imagine you are trying to bake the perfect cake. You have numerous ingredients: flour, sugar, eggs, baking powder, etc. Instead of focusing on the specific amounts of each ingredient (which could vary widely), Buckingham’s Pi theorem suggests creating ratios of ingredients that matter most to achieve the desired cake texture. This way, you can simplify your recipe and still bake a great cake regardless of the specific measurements you start with.
Dimensional Analysis and Grouping
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To apply Buckingham's Pi theorem, identify the dependent and independent variables within the problem and determine their basic dimensions (mass, length, time).
Detailed Explanation
To utilize Buckingham's Pi theorem effectively, first identify the variables involved in the experiment and classify them as dependent or independent. For instance, in our drag force example, you would classify drag force as a dependent variable affected by diameter, velocity, density, and viscosity, which are independent variables.
Next, determine the fundamental dimensions of each variable. For example, mass (M) is typically expressed in kilograms, length (L) in meters, and time (T) in seconds. Using these dimensions, you can create dimensionless groups (Pi terms) to analyze relationships without specific units, simplifying complex equations into more manageable ones.
Examples & Analogies
Consider a car engine's performance. You want to evaluate its efficiency based on fuel consumption (dependent variable) while considering the type of fuel, speed, and engine size (independent variables). Instead of measuring each aspect in gallons, horsepower, or liters, you can convert them into dimensionless terms based on ratios like kilometers per liter (efficiency) that relate directly to performance, allowing for quick assessments without the confusion of various unit systems.
Deriving Dimensionless Groups
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Once the dependent and independent variables are identified, apply the theorem to derive dimensionless groups that simplify the relationship between these variables.
Detailed Explanation
Using the previously identified variables, you now construct dimensionless groups according to Buckingham's Pi theorem. Each group is formed by multiplying variables in such a way that any units cancel out, resulting in dimensionless quantities. For instance, you might create a dimensionless drag coefficient (CD) that relates drag force to other factors like fluid density and velocity in a formula like CD = F/(0.5 * rho * V^2 * A), where A is the area of the sphere.
This allows engineers to create a generalized equation that can predict the drag force for any diameter or speed without recalculating for every unique case, because each group captures essential physics without reliance on dimensions.
Examples & Analogies
Think of how chefs might use ratios to create sauces. If a chef uses a ratio of ingredients that creates a certain flavor profile, they can replicate that flavor with different ingredient measurements. Similarly, using dimensionless groups, engineers can maintain consistency in performance across variable scales, much like a recipe that works with various quantities yet yields the same tasty sauce.
Number of Dimensionless Groups
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The number of independent dimensionless groups is determined by subtracting the number of fundamental dimensions from the total number of variables involved.
Detailed Explanation
The number of independent dimensionless groups can be calculated through the formula n - k, where n represents the total number of variables and k is the number of fundamental dimensions (mass, length, time). For example, if we have five variables in our drag force experiment (drag force, diameter, velocity, density, viscosity) and the three basic dimensions, the calculation would yield 5 - 3 = 2 independent dimensionless groups. This informs researchers about how many unique relationships they can establish from their analyses, streamlining their experimental design.
Examples & Analogies
Picture a classroom where students can submit multiple projects. If each project represents a different variable in a study, subtracting the basic subjects (Math, Science, Art) from the total projects tells you how many different topics or approaches can arise from shared principles. Just as each project might lead to unique outcomes under the same educational framework, dimensionless groups allow multiple solutions or insights based on core scientific laws governing the relationships.
Application and Importance
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Applying Buckingham's Pi theorem leads to significant time and resource savings in experimental studies, enabling more efficient data interpretation and analysis.
Detailed Explanation
By applying Buckingham's Pi theorem, researchers can conduct fewer experiments while gaining equivalent data insights. It enables them to create a set of dimensionless curves that can represent relationships for various conditions without running each unique scenario individually. This efficiency not only saves time but also resources, making it cost-effective, especially in fields like fluid mechanics where experiments can be extensive and complex.
Examples & Analogies
Consider how scientists study weather patterns. Instead of measuring every possible variable for each weather condition—temperature, humidity, pressure—they develop models based on simplified relationships that help predict weather forecasts across varying situations. Similarly, Buckingham's Pi theorem helps streamline complex experimental designs into manageable analyses, allowing researchers to obtain reliable results and predictions swiftly.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Dimensional Homogeneity: The requirement that equations maintain consistent dimensions across all terms.
-
Buckingham's Pi Theorem: A method for reducing the complexity of multiple variables in dimensional analysis.
-
Dimensionless Groups: Constructing groups of variables that eliminate units, simplifying relationships.
-
Reynolds Number: A critical dimensionless parameter used for describing flow regimes in mechanics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Describing the drag force on a sphere using diamond dimensions of diameter, velocity, and viscosity.
-
Using Buckingham's theorem to relate multiple fluid flow experiments to a single dimensionless group, reducing the number of experiments needed.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
If the units don’t align, your experiments may misdefine.
📖 Fascinating Stories
-
Imagine a scientist working tirelessly to test fluid flows. With so many combinations, they'll go broke! But with Buckingham, they find the right dimensions and can run fewer tests with clear conclusions.
🧠 Other Memory Gems
-
PIG - Pi (independent groups), n - variable count, k - dimensional types. This helps remember the key aspects of Buckingham’s theorem.
🎯 Super Acronyms
DIM - Dimensional Identities Matter. This reminds us of the importance of dimensional analysis.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Dimensional Homogeneity
Definition:
The principle that states that all terms in an equation must have the same dimensions.
-
Term: Buckingham’s Pi Theorem
Definition:
A theorem in dimensional analysis that states the number of dimensionless parameters (Pi terms) is equal to the number of variables minus the number of fundamental dimensions.
-
Term: Dimensionless Group
Definition:
A group of variables that can be expressed in such a way that they do not have any dimensions.
-
Term: Reynolds Number
Definition:
A dimensionless number that describes the flow characteristics in fluid dynamics, representing the ratio of inertial forces to viscous forces.