Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Dimensional Homogeneity
Unlock Audio Lesson
Today, we're diving into dimensional homogeneity. Can anyone tell me what dimensional homogeneity means?
I think it means that all terms in an equation have to have the same dimensions.
Exactly! For an equation to be valid, both sides must be dimensionally homogeneous. This ensures that when you perform calculations, the units cancel or agree correctly. Can anyone give an example of how we check for dimensional homogeneity?
For example, in the equation for pressure, we can check if it equals force per area, which would be mass times acceleration over area.
Great example! The units must match across the equation. Let’s summarize: Dimensional homogeneity helps validate equations in fluid mechanics.
Understanding Buckingham's Pi Theorem
Unlock Audio Lesson
Now, let's talk about Buckingham's Pi Theorem. Who can explain its significance?
It helps us determine the number of dimensionless groups we need for our experiments, right?
Exactly! If we have `n` variables and `k` fundamental dimensions, we can calculate the number of independent dimensionless groups as `n - k`. Why do we care about dimensionless groups?
They let us reduce the number of tests we need to perform when designing experiments!
Correct! Knowing how many groups we need streamlines our experimental process. Let's remember: `Pi groups` can reveal relationships between different fluid behaviors.
Application of Non-Dimensional Analysis
Unlock Audio Lesson
Next, let’s discuss practical applications of non-dimensional analysis. Can anyone think of examples where this is beneficial?
The Reynolds number is a big one! It helps us predict flow types.
Perfect! The Reynolds number is derived from dimensional analysis and helps determine whether a flow is laminar or turbulent. How does this impact our understanding?
It helps engineers optimize designs to control flow and reduce drag!
Absolutely, reducing drag is crucial for efficiency. Summarizing today, non-dimensional analysis not only simplifies relationships in fluid mechanics but also saves costs and time in experiments.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, non-dimensional analysis is explored as a powerful tool in fluid mechanics to design experiments and derive relationships between variables using dimensional homogeneity and Buckingham's Pi Theorem. The importance of dimensionless groups in improving experimental efficiency and data interpretation is highlighted.
Detailed
Detailed Summary
Non-dimensional analysis is a critical approach used in fluid mechanics that simplifies complex equations and experiments by removing units of measurement. This section focuses on the following key concepts:
Dimensional Homogeneity
Dimensional homogeneity states that all terms in a physical equation must have the same dimensions. In practice, this allows engineers and scientists to verify if equations are set up correctly by ensuring that both sides of the equation can be expressed in terms of the same basic dimensions: mass (M), length (L), and time (T).
Buckingham's Pi Theorem
The Buckingham Pi Theorem is fundamental in non-dimensional analysis, stating that if there are n variables in a problem, and k fundamental dimensions, the number of independent dimensionless groups (π groups) can be found using the formula: \( π = n - k \). This theorem provides a systematic method for deriving dimensionless quantities which can be used in experimental analysis, significantly reducing the number of experiments needed to explore relationships between variables.
Applications in Fluid Mechanics
Examples are presented on how dimensionless numbers like the Reynolds number, which helps predict flow patterns and drag on objects in a fluid, are derived using non-dimensional analysis. This process not only aids in designing experiments more efficiently but also enhances a deeper understanding of the fluid behaviors without requiring extensive model testing.
In summary, non-dimensional analysis stands as a vital part of fluid mechanics, facilitating innovation in experimental design and data interpretation by using dimensionless parameters to relate various fluid properties.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Non-Dimensional Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we will come to the dimensionless groups. I think these are quite well-known, even at the class 11th or 12th levels. So basic dimensions are mass, length, and time. These are the three basic dimensions: mass, length, and time.
Detailed Explanation
Non-dimensional analysis is a technique that simplifies the analysis of physical phenomena by removing units from equations and results, making them easier to interpret and compare. The primary dimensions involved in such analyses are mass (M), length (L), and time (T). By focusing on these fundamental parameters, scientists and engineers can derive relationships and understand systems more universally, regardless of the specific units used.
Examples & Analogies
Think of non-dimensional analysis like cooking a recipe. The ingredients are like the basic dimensions: you can have flour (mass), water (volume/length), and time (how long you cook). If you make the same dish in different quantities (scales), as long as you keep the proportions the same, the dish will turn out fine. Similarly, in fluid mechanics, if we can formulate our equations in a non-dimensional way, we can understand the flow regardless of the scale of our model.
Basic Dimensions and Fluid Properties
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Fluid properties are related to dimensions, such as length, area, and volume. Length is L1, L2, and area is L2, while volume is L3. You can understand what velocity is: length per time.
Detailed Explanation
In fluid mechanics, understanding fluid properties such as velocity, kinematic viscosity, and strain rate is essential. Velocity is defined as the distance traveled over time, which can be expressed as length (L) over time (T). For larger-scale phenomena like the behavior of fluids in pipes or around objects, knowing how to express these relationships dimensionally and non-dimensionally helps in ensuring that experiments or simulations will yield similar results under varying conditions.
Examples & Analogies
Consider a river and a garden hose—both involve water flowing, but the flow rates (velocities) differ vastly. By understanding the critical dimensions affecting their flow (like width and pressure), we can predict how water behaves in each case, even if we have not directly measured every scenario.
Principles of Dimensional Homogeneity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Most equations in engineering are dimensionally homogeneous. This means that the dimensions of the left-hand side (LHS) of an equation should match those of the right-hand side (RHS).
Detailed Explanation
Dimensional homogeneity is the principle that dictates that for an equation to be valid, the dimensions of all terms must be consistent. This principle is critical for engineers and scientists to ensure that their equations are valid representations of physical laws. If an equation is not dimensionally homogeneous, it indicates a flaw in the formulation, helping to catch errors before physical trials.
Examples & Analogies
Imagine trying to bake a cake and your recipe calls for ingredients by weight (like flour in grams) while your measuring scale only measures volume (like liters). If you mixed measures without consistent units, your cake may not turn out right! Similarly, in physics, maintaining consistent dimensions ensures the equations behave as expected.
Non-Dimensional Groups and Experiments
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
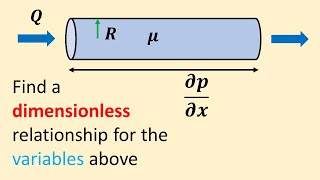
If we look at the fluid flow and drag force, it could depend on variables like diameter D, velocity V, density ρ, and dynamic viscosity μ. You can conduct fewer experiments by using dimensional analysis to identify the relationships among these variables.
Detailed Explanation
Using non-dimensional groups allows for the reduction of experimental complexity. Instead of conducting numerous experiments for every possible variable combination, dimensional analysis helps in developing correlation equations by identifying key dimensionless parameters, such as the Reynolds number. This key parameter simplifies the situation by providing the same results regardless of the specific scales of the system, thereby saving time and resources.
Examples & Analogies
Think of an athlete running a race. Different athletes (D) may run at varying speeds (V) and face different conditions (ρ and μ -- like wind resistance). If we can define a dimensionless factor such as the speed-to-resistance ratio, it gives us a clearer view of performance across different scenarios without needing to compare every individual athlete in every condition.
Buckingham's Pi Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Buckingham's pi theorem states that if there are n dependent variables, the number of independent dimensionless groups we can generate is n - 3. This helps in further simplifying experiments.
Detailed Explanation
The Buckingham Pi theorem provides a systematic method to derive dimensionless numbers from physical problem statements involving multiple variables. It emphasizes that only a subset of combined variables needs to be studied in-depth, which makes study design efficient and allows researchers to focus on more significant parameters. This theorem supports the idea that by understanding these relationships, researchers can derive broader principles applicable across different scenarios.
Examples & Analogies
Consider a team preparing for a sports event—rather than assessing the individual performance of every athlete in every condition, they could focus on key metrics like speed, endurance, and skill levels. In doing so, they develop techniques that apply to a wide range of performances, much like reducing the complexity of fluid dynamics using the Buckingham Pi theorem.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Dimensional Homogeneity: Ensures all terms in equations have the same dimensions, facilitating accurate calculations.
-
Buckingham's Pi Theorem: Provides a systematic method to determine the number of independent dimensionless groups.
-
Dimensionless Groups: These quantities allow for simpler relationships between variables in fluid mechanics.
-
Reynolds Number: A crucial dimensionless group for understanding flow patterns and types.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using dimensional analysis to derive the Reynolds number to study flow characteristics.
-
Designing experiments with fewer variations by applying Buckingham's Pi Theorem.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Dimensionally homogenous, equations must agree, Left-hand and right-hand both must be free.
📖 Fascinating Stories
-
Imagine an engineer trying to measure water flow. He notes that without making measurements dimensionless, comparing different systems is like speaking different languages—no one understands each other!
🧠 Other Memory Gems
-
To remember Buckingham's Pi Theorem: N - K = π (N = number of variables, K = dimensions). Think: 'No K, No Pi!'
🎯 Super Acronyms
PIG
- Pi's Independent Groups - helps remember that you can isolate independent influences through dimensional analysis.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Dimensional Homogeneity
Definition:
A principle stating that all terms in a physical equation must have the same dimensions.
-
Term: Buckingham's Pi Theorem
Definition:
A theorem that states the number of independent dimensionless groups in a problem can be calculated as the difference between the number of variables and fundamental dimensions.
-
Term: Dimensionless Group
Definition:
A quantity without physical units that helps relate different variables in an equation.
-
Term: Reynolds Number
Definition:
A dimensionless group used to predict flow patterns in fluid dynamics.
-
Term: Fluid Mechanics
Definition:
The branch of physics concerned with the behavior of fluids at rest and in motion.