Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Dimensional Analysis
Unlock Audio Lesson
Today we are delving into dimensional analysis, a vital tool in fluid mechanics. Can anyone tell me what the basic dimensions are?
Isn’t it mass, length, and time?
Exactly! We denote them as M, L, and T. Now, why do you think these dimensions are important?
They help in describing fluid properties, right?
Correct! They allow us to express everything from velocity to pressure. Let’s remember the acronym V = L/T to recall how velocity relates to these dimensions.
How do we apply these dimensions in experiments?
Great question! By ensuring dimensional homogeneity, we can simplify complex equations. Remember, dimensional analysis helps us create general equations applicable across different scenarios.
Dimensional Homogeneity and Its Importance
Unlock Audio Lesson
Let’s talk about dimensional homogeneity. What does it mean when we say an equation is dimensionally homogeneous?
It means all terms in the equation should have the same dimension.
Exactly! This ensures that our equations are physically meaningful. If we make a mistake in dimensions, what could happen?
The results could be incorrect or meaningless.
Precisely! Always check your equations for dimensional consistency. It’s like a safety check in engineering.
Introduction to Buckingham's Pi Theorem
Unlock Audio Lesson
Now, let’s explore Buckingham's pi theorem. Can someone summarize what this theorem helps us find?
It helps us identify independent dimensionless groups from a list of variables?
Exactly! For instance, if we have four variables and three fundamental dimensions, how many dimensionless groups can we form?
One dimensionless group, I think?
Close! In general, we can derive the dimensionless groups as 'n - r', where 'r' is the number of basic dimensions. So if we have four variables and three basic dimensions, we’d have one dimensionless group.
Application of Dimensionless Groups
Unlock Audio Lesson
Why do we utilize dimensionless groups in experimental designs?
To simplify the number of experiments needed?
Correct! By using dimensionless groups like the Reynolds number, we can predict flow behavior without massive test setups.
So, if we derive a relationship in one scenario, we can apply it across others?
Exactly! This concept saves us time and resources, especially in fluid mechanics. Think of it as finding shortcuts to complex problems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section covers the importance of dimensionless groups in understanding fluid mechanics, explaining how dimensional analysis can simplify experiments and lead to universal correlations. Buckingham's pi theorem is highlighted as a critical tool for deriving dimensionless groups.
Detailed
Dimensionless Groups
In fluid mechanics, dimensional analysis is crucial for simplifying complex scenarios into dimensionless groups. This section elaborates on the concept of dimensional homogeneity, which asserts that all terms in a physical equation must have the same dimensions. The universality of fluid flow phenomena can be expressed through dimensionless numbers such as Reynolds number and others.
Key Points:
- Basic Dimensions: In fluid mechanics, the fundamental dimensions are mass (M), length (L), and time (T). These dimensions form the basis for all fluid properties, from velocity to viscosity.
- Fluid Properties: Properties such as velocity, pressure, and shear stress are expressed in terms of these basic dimensions, leading to a better understanding of their interrelations.
- Dimensional Homogeneity: This principle states that every equation in fluid mechanics should be dimensionally consistent, with each term having compatible units.
- Buckingham's Pi Theorem: This theorem underpins the dependence of physical phenomena, allowing the derivation of dimensionless groups that simplify experimental work.
By employing dimensionless groups, researchers can predict fluid behavior across different scales without conducting extensive individual experiments. This leads to a more efficient study of fluid dynamics.
Youtube Videos
![Common Dimensional group in fluid mechanics @PrakashAcademy [IITK]](https://img.youtube.com/vi/UP1n4Ohe-nY/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Basic Dimensions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Even at the class 11th or 12th levels. So basic dimensions what we have mass length and the time these are 3 basic dimensions mass, length and time. So what we have when we would do a theoretic analysis or the experiment analysis can be made universal okay that is what exactly highlighting here independent of its specific locations using a diverse group to express them.
Detailed Explanation
In fluid mechanics, we often deal with measurements and calculations involving three basic dimensions: mass, length, and time. These dimensions are essential because they help us describe the physical quantities in a universal way. When we conduct experiments or theoretical analyses, we aim for the results to be applicable in various scenarios, regardless of the specific conditions of the experiment. For example, knowing how mass, length, and time relate to each other allows us to convert units and understand the behavior of fluid systems under different conditions.
Examples & Analogies
Think of these basic dimensions like the ingredients for a recipe. Just as you need flour (mass), water (length), and time to bake bread, in scientific experiments, you need mass, length, and time to analyze fluid behavior accurately. If you know the relationships among these 'ingredients', you can replicate a successful recipe (or experiment) in different kitchens (or environments).
Fluid Properties and Dimensional Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look at the fluid properties what we have some of the fluid properties if you know it is related to the dimensions okay that is the length area and the volume. So it is just a dimension and geometric dimensions so it has only unit in terms of the length okay. So that means length is L1 L2 and area will be L2 the volume will be L3 so you can understand what is the velocity you know it length power unit time.
Detailed Explanation
Fluid properties such as length, area, volume, velocity, and acceleration can all relate back to the basic dimensions. For instance, volume is calculated as length cubed (L^3), area as length squared (L^2), and velocity is defined as length over time (L/T). Knowing how different properties are represented dimensionally helps us understand their relationships and allows for calculations in fluid dynamics. This connection between properties and dimensions is crucial in analyzing and predicting fluid behavior.
Examples & Analogies
Imagine a water bottle: its volume tells you how much water it can hold (which is tied to the length of each side). If you know the dimensions of the bottle, you can quickly calculate how much liquid it can contain. Similarly, in fluid mechanics, understanding the dimensions of fluid properties makes it easier to analyze systems, like predicting how fast water will flow through a pipe based on its diameter (length) and how long it has been flowing (time).
Principle of Homogeneity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us go for what is the principal of homogeneity all the equations not all the equations so most of the questions in engineering the most of the equations of engineering dimensionally homogenous not all that is the let me have a repeat these things that means what it indicates as that the dimensions of the equations will be the same okay the left side of dimensions LHS should have a dimensions of right hand side.
Detailed Explanation
The principle of homogeneity in engineering states that equations must have the same dimensions on both sides. This means if you are analyzing forces, velocities, and other quantities in fluid mechanics, the dimensions represented by the variables used must balance out. For example, if we're looking at drag force, the expression on one side of the equation must equate to the drag force's dimensions represented on the other side. This principle is fundamental because it ensures that the equations we derive are valid and meaningful.
Examples & Analogies
Think of it like a balanced scale. When you're weighing two objects, both sides need to hold items that can be measured similarly—if one side has apples and the other has oranges, the scale won't balance. Similarly, in fluid mechanics equations, keeping the dimensions balanced ensures our calculations are correct, much like ensuring a recipe is balanced in ingredients for the perfect cake.
Reynolds Number and Dimensional Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
You just substitute it and try to find out the Reynolds number which is a well-known equations which we call the Reynolds equations. So okay Reynolds numbers okay we will discuss more about that in pipe flow and so if we look at that what I developed now I instead of F functions we are looking at G functions which is a really sensitive tool non-dimensional group. One is left side and the right side this would have the same and I will be looking at different functions if it that did the conditions.
Detailed Explanation
The Reynolds number is a dimensionless quantity that helps predict flow patterns in different fluid flow situations, such as laminar or turbulent flow. By using dimensional analysis, we can derive this number based on a combination of the relevant fluid properties (such as velocity, density, and viscosity). The beauty of non-dimensional numbers like the Reynolds number is that they allow us to critically analyze fluid behavior without the need for extensive experimentation because they offer a universal understanding applicable to various scenarios.
Examples & Analogies
Consider trying to understand the traffic flow at an intersection. If you think about cars (fluid) moving at a certain speed and how that is affected by the size of the intersection (diameter) and how dense the traffic is (density), you can gauge whether the flow will be smooth or chaotic (laminar or turbulent). The Reynolds number acts like a traffic signal, guiding us on whether we need to prepare for a smooth cruise or a bottleneck!
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Basic Dimensions: Mass (M), Length (L), Time (T) are the foundational dimensions in fluid mechanics.
-
Dimensional Homogeneity: All equations must be dimensionally consistent, meaning all terms have the same dimensions.
-
Buckingham's Pi Theorem: A way to derive dimensionless groups by considering the number of independent variables and fundamental dimensions.
-
Reynolds Number: A critical dimensionless group that helps predict flow conditions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
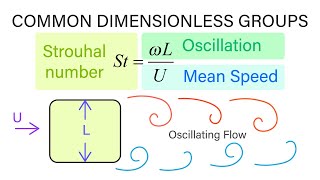
An example of a dimensionless group is the Reynolds number, calculated using parameters like fluid density, speed, and characteristic length.
-
In experiments, using dimensionless groups allows simplifications, which reduces the number of tests required—such as varying the diameter of a cylinder in fluid flow studies.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When you analyze dimensions with care,
📖 Fascinating Stories
-
Imagine a scientist designing an experiment. He learns that to simplify his tests, he must ensure that every measurement—mass, length, and time—aligns perfectly, like pieces of a puzzle fitting together in harmony.
🧠 Other Memory Gems
-
Remember the acronym MLT for Mass, Length, Time; it’s fundamental in fluid mechanics.
🎯 Super Acronyms
Use the acronym BLT
- Basic Length Time to remember the dimensions in fluid mechanics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Dimensionless Group
Definition:
A quantity that has no physical dimensions and is derived from physical variables, allowing for easier comparisons and analyses.
-
Term: Dimensional Homogeneity
Definition:
A principle stating that all terms in an equation must have the same dimensional representation.
-
Term: Buckingham's Pi Theorem
Definition:
A method for deriving dimensionless numbers from physical equations based on the number of variables and dimensions involved.
-
Term: Reynolds Number
Definition:
A dimensionless number that indicates the type of flow (laminar or turbulent) based on fluid properties and flow conditions.