Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Drag Forces
Unlock Audio Lesson
Alright, everyone! Today, we are diving into drag forces. Can anyone tell me what drag force refers to?
Isn't it the resistance an object experiences when moving through a fluid?
Exactly! It's the force that opposes the motion of an object through a fluid. Now, why is it so important to analyze drag force?
Because it affects how fast or how efficient an object can move through water or air?
Correct! Analyzing drag forces helps engineers design vehicles and structures efficiently. Let's now move to how we can represent and compute drag forces quantitatively.
Dimensional Analysis
Unlock Audio Lesson
One core principle in fluid mechanics is dimensional homogeneity. Can anyone explain what that means?
I think it means that both sides of an equation must have the same dimensions, right?
Spot on! This principle ensures that the equations we use to compute drag forces are valid. Let's take an example of drag force calculated for a cylinder in airflow.
How do we express that mathematically?
We can express it using basic dimensions: mass, length, and time. Remember M for mass, L for length, and T for time. Knowing these basics helps in dimensional analysis.
Buckingham's Pi Theorem
Unlock Audio Lesson
Now, let's discuss Buckingham's Pi theorem. Why do you think it's vital in fluid mechanics?
Because it allows us to simplify complex problems by reducing variables?
Exactly! It helps us form dimensionless groups which can represent the relationship between physical quantities. What would be an example of a dimensionless number in fluid mechanics?
The Reynolds number?
Yes! The Reynolds number is essential for characterizing flow regimes. Remember, dimensional analysis aids in understanding how different systems correlate.
Experimental Design
Unlock Audio Lesson
Let's connect everything by talking about designing experiments. Why would we want to reduce the number of experiments needed?
To save resources and time!
Right! Using dimensional analysis allows us to conduct fewer experiments by focusing on critical relationships. Can anyone summarize how to use dimensional analysis in our experimental design?
We can identify independent and dependent variables, apply Pi theorem, and derive relationships that minimize the number of tests needed.
Great summary! This method can lead to more effective studies while saving us significant time and effort.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Drag force analysis is crucial in fluid mechanics for understanding how objects interact with fluid flows. This section dissects the importance of dimensional homogeneity, introduces Buckingham's Pi theorem, and demonstrates how to apply these concepts through experimental design and analysis.
Detailed
Drag Force Analysis
Drag force plays a significant role in fluid mechanics, especially in the design and analysis of experiments involving fluid flow around objects. Understanding the relationship between drag force and various fluid properties is essential for predicting the behavior of objects in a fluid medium. This section emphasizes the following key concepts:
1. Dimensional Homogeneity
Dimensional homogeneity refers to the principle that equations must be dimensionally consistent, meaning both sides of the equation must have the same dimensions. For instance, when analyzing drag forces, the relationship can be expressed in terms of basic dimensions such as mass (M), length (L), and time (T).
2. Drag Force Calculation
The drag force acting on objects like cylinders in fluid flow can be calculated using pressure coefficients which depend on the object's geometry, the fluid's density and viscosity, and the flow velocity. The formula for the pressure coefficient (Cp) is introduced to facilitate these calculations.
3. Dimensionless Groups
The section discusses the creation of dimensionless groups using Buckingham’s Pi theorem, which helps reduce the complexity of the analysis and streamline the experimental design process. Dimensionless variables enable comparisons between different systems and flows, thereby enriching the understanding of drag behavior across various scenarios.
4. Experimental Design
Understanding how to design experiments to measure drag force is illustrated, highlighting the importance of conducting fewer experiments through the application of dimensional analysis. This leads to significant time and cost savings while still enabling robust experimental outcomes.
By synthesizing these concepts, the section highlights the theoretical framework and practical applications of drag force analysis in fluid mechanics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Drag Force
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we will come to the dimensionless groups I think these quite you know it. Even at the class 11th or 12th levels. So basic dimensions what we have mass length and the time these are 3 basic dimensions mass, length and time.
Detailed Explanation
In fluid mechanics, understanding the basic dimensions—mass, length, and time—is essential. These dimensions form the foundation of how we describe physical phenomena, including the forces acting on objects in a fluid. For example, when analyzing drag force, we need to consider the mass of the fluid, the length of the object (like a cylinder), and the time over which the fluid flows. This helps us create relationships between these variables and conduct proper experiments.
Examples & Analogies
Imagine you're riding a bicycle. The mass of you and your bike affects how fast you can go through the air (which is like the fluid in this case). Additionally, the size of the bike (length) and how long you pedal (time) all impact how much air pushes back on you—the drag force. Understanding these dimensions helps us predict how to improve speed and efficiency.
Understanding Fluid Properties
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The acceleration similar way you can do it let me look at what is the distance or volumetric rate volume or unit time that is what we Lq divide by That will be the volumetric then now we have come to the 2 different parts one is Kinematic viscosity as we discuss in newtons laws of viscosity is that it is independent of mass.
Detailed Explanation
Fluid properties like kinematic viscosity are critical in drag force analysis. Kinematic viscosity measures a fluid's resistance to flow and is expressed in the dimensions of length and time only—making it independent of mass. This means that when considering drag force, the speed of the fluid and its viscosity play a significant role in determining how much force will act on a body moving through that fluid.
Examples & Analogies
Think of kinematic viscosity as the 'thickness' of a fluid, like honey compared to water. Honey is thicker (has higher viscosity) and will create more drag on a moving object than water. When you push through honey, you feel more resistance than when you push through water, illustrating how different viscosities can significantly affect drag force.
Calculating Drag Force
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
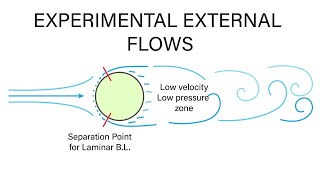
So the drag force what is happening is it is a function of D is the diameter of the cylinder V is the velocity of the flow. And the rho and the mu is the fluid properties related to density and the dynamic viscosities the viscous force components.
Detailed Explanation
To calculate the drag force on a cylinder in a fluid, we need to consider various factors including the diameter of the cylinder (D), the flow velocity of the fluid (V), the density of the fluid (ρ), and the dynamic viscosity of the fluid (μ). This relationship shows that as the diameter increases, or the velocity increases, or depending on the fluid's properties, the drag force will change accordingly. This is essentially an application of dimensional analysis, where we derive relationships between various forces and parameters.
Examples & Analogies
Imagine you're trying to push a large beach ball through a pool. The bigger the ball (larger diameter), the more difficult it becomes to push it through the water, especially if you're trying to do so fast (higher velocity). The thickness of the water (its viscosity) also matters—if the pool is filled with thick syrup, it would be much harder to push the ball than in normal water. This real-world experience reflects the principles described in drag force calculations.
Dimensional Analysis and Experimental Design
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So the non-dimensional experiments making us that we can make a dimensionless force plot. And we can conduct the experiment with the different Reynolds numbers and plot because once you do with different Reynolds experiment you will get the course you know the velocity you move the diameters of the cylinders then you can compute it what will be the non dimensionless force component here.
Detailed Explanation
Dimensional analysis helps simplify experiments by allowing researchers to create dimensionless groups, such as Reynolds numbers, which relate the drag force to other fluid characteristics. By conducting experiments across a range of Reynolds numbers, scientists can plot curves of non-dimensional forces, allowing them to predict behavior in different scenarios without needing to perform every possible combination of tests beforehand.
Examples & Analogies
Consider baking cookies. You don’t need to bake every possible combination of ingredients to know what will taste best. Instead, you might use a standard recipe and test a few variations. Similarly, by understanding the fundamental relationships through dimensional analysis, researchers can reduce the number of experiments while still obtaining useful and predictive results about drag forces in different fluid flows.
The Importance of Dimensionless Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Almost all the time do any experimentalists they start designing this experiment using dimensional analysis.
Detailed Explanation
Dimensionless analysis is a critical component in experimental design across many fields, including fluid mechanics. By reducing complex relationships into basic dimensionless numbers, researchers can conduct more efficient experiments, gather predictive data, and make sense of their results more effectively. This analytical approach significantly enhances the understanding of fluid dynamics.
Examples & Analogies
Imagine a sports coach trying to train players of different skill levels. Instead of creating unique drills for each player, the coach devises a series of drills that emphasize fundamental skills relevant to all players. This way, the coach saves time and resources while improving skill development. In fluid mechanics, dimensionless analysis provides a similar efficiency, helping scientists and engineers design impactful experiments without redundancy.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Dimensional Homogeneity: Ensures equations are dimensionally consistent.
-
Drag Force Calculation: Method of computing drag forces using various parameters.
-
Dimensionless Groups: Formulated using Buckingham’s Pi theorem for simplifying analysis.
-
Experimental Design: Importance of reducing experiments through dimensional analysis.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Calculating the drag force on a cylinder in airflow using pressure coefficients.
-
Using Reynolds number to understand the behavior of fluid flow around different shapes.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Drag force, it slows you down, in water or air, it wears a frown.
📖 Fascinating Stories
-
Imagine a fish swimming upstream; it faces drag from water currents, making the journey tougher. But with the right understanding of forces, it can navigate efficiently!
🧠 Other Memory Gems
-
To remember dimensionless groups: Remember 'Pioneer Friends Name Valiant Rivals' (Pi, Fluid properties, Number, Velocity, Resistance).
🎯 Super Acronyms
D.R.A.G - Dimension, Resistance, Airflow, Geometric shape.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Drag Force
Definition:
The resistance force encountered by an object moving through a fluid.
-
Term: Dimensional Homogeneity
Definition:
The principle stating that all terms in an equation must have the same dimensions.
-
Term: Buckingham’s Pi Theorem
Definition:
A theorem used for dimensional analysis that allows the reduction of physical variables to dimensionless groups.
-
Term: Reynolds Number
Definition:
A dimensionless quantity used to predict flow patterns in different fluid flow situations.