Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Dimensional Analysis
Unlock Audio Lesson
Today, we will dive into the world of dimensional analysis. This tool helps us relate different physical quantities by incorporating their dimensions.
What do you mean by dimensions, and why are they important?
Great question! Dimensions like length, time, and mass provide the fundamental building blocks for equations. Without them, we could not make sense of how variables interact.
So, all variables in fluid flow must have dimensions?
Exactly! In fluid mechanics, we typically use repeating variables such as length, velocity, and viscosity. Let's remember them with the mnemonic 'L V V' - Length, Velocity, and Viscosity.
How do we transform these into non-dimensional forms?
That's where we use π groups! These are combinations of our variables that yield a dimensionless value. For example, let's consider the Reynolds number.
What's special about the Reynolds number?
The Reynolds number helps us determine the flow regime, whether it is laminar or turbulent, based on the ratio of inertial and viscous forces. Remember: 'Reynolds relates inertia to viscosity!'
To summarize, dimensional analysis is crucial in fluid mechanics for understanding and simplifying complex interactions.
Understanding Reynolds Number
Unlock Audio Lesson
Now we’ll explore Reynolds number in detail. What does it represent?
Isn’t Reynolds number the ratio of inertial forces to viscous forces?
Absolutely! And as we measure flow conditions, it helps us identify critical phenomena in fluid dynamics. A low Reynolds number means smooth, orderly flow, while a high value indicates turbulence.
Can you give an example of where this is used?
Sure! Take blood flow in arteries; under normal conditions, we expect a laminar flow, reflected by a low Reynolds number.
What happens if that number increases?
Good question! An increased Reynolds number can lead to turbulence, introducing chaotic behavior in the flow, which could affect transport and mixing.
In summary, the Reynolds number is key in determining flow regimes and impacts practical scenarios significantly.
Introduction to Froude Number
Unlock Audio Lesson
Next, let's discuss Froude number. This dimensionless number compares the inertia forces to gravitational forces. Who can explain its relevance?
It would be important in situations involving waves or free-surface flows, right?
Exactly! For example, in dam spillways, when we analyze overflow, the Froude number gives insight into how gravity influences fluid motion.
How do we calculate it?
The formula is Fr = v / sqrt(gL), where 'v' is the flow velocity, 'g' is gravitational acceleration, and 'L' is the characteristic length. Keep in mind the acronym 'FGI' - Froude Gravitational Inertia.
What about when the Froude number changes?
When Fr is less than one, gravity dominates, leading to tranquil flow; greater than one indicates dominance of inertial forces, which can produce turbulence.
To summarize, the Froude number helps us analyze and predict the behavior of fluids under various conditions.
Other Dimensionless Numbers
Unlock Audio Lesson
Now let’s discuss additional dimensionless numbers, such as Weber and Euler numbers. Who can tell me what these represent?
Weber number compares inertial forces to surface tension, right?
Correct! This number is crucial in scenarios like droplet formation. We also have the Euler number, which compares pressure forces to inertial forces.
Could you provide practical examples of where they're applied?
Definitely! The Weber number is vital in analyzing spray atomization in engines, while the Euler number is often referenced in turbomachinery to ensure structural integrity.
Can we derive any relationships from these numbers?
Certainly! Many engineering problems can establish correlations based on these non-dimensional forms, which simplify complex interactions.
To summarize, Weber and Euler numbers complement our understanding of fluid dynamics by giving insights into surface and pressure-driven phenomena.
Dimensional Analysis Examples
Unlock Audio Lesson
Finally, let's look at some specific examples of dimensional analysis in practice. Can anyone provide an example of a scenario where we apply dimensional analysis?
What about volumetric discharge as a function of radius, dynamic viscosity, and the gradient of pressure?
Excellent! In this case, we have Q as volumetric discharge, with various interdependent variables. How would we start analyzing this?
We would identify the dimensions of all variables involved.
Exactly! Each has its dimensions, and we can derive several independent dimensionless groups from this. It’s crucial for fluid dynamics.
How do we ensure that our derived groups are correct?
We validate them through substitution into the dimensional analysis equation and ensure they maintain dimensionless integrity!
To summarize, examples in dimensional analysis help demonstrate how to simplify and understand complex relationships among fluid properties.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section provides a comprehensive overview of dimensional analysis in fluid mechanics, emphasizing the significance of non-dimensional forms. It discusses different repeating variables, the use of dimensionless groups like Reynolds and Froude numbers, and offers examples to illustrate these concepts for easy understanding.
Detailed
Detailed Summary
Dimensional analysis is an essential method in fluid mechanics used to derive relationships between variables. This section begins by introducing the repeating variables in fluid mechanics, including length, velocity, and viscosity. The concept of non-dimensional forms such as π groups is evaluated, specifically in relation to identifying patterns and simplifying equations within fluid flow problems.
Key number groups are discussed:
- Reynolds Number: A ratio indicating the relative importance of inertial forces to viscous forces in fluid flow, essential for differentiating between laminar and turbulent flow.
- Froude Number: A dimensionless number comparing inertia forces to gravitational forces, crucial for analyzing free surface flows and waves.
- Weber and Euler Numbers: These include comparisons of inertia forces to surface tension and pressure changes, respectively, vital for understanding phenomena like cavitation.
Furthermore, examples illustrating independent dimensional groups clearly demonstrate how different fluid characteristics can be combined and analyzed through the lens of dimensional analysis. By using foundational variables and transforming them to dimensionless forms, one gains a clearer understanding of the principles underlying fluid mechanics, ultimately allowing for effective exploration of real-world applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Dimensional Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now to look at that this is a called a theorem it is a very easy concept that though please do not have a conclusion with the means 3.14 it is a non dimensionless form of p is okay. So if it is that I can have a 3 variables okay that is the length velocity and the force these are called the repeating variables length velocity and viscosity I will put the repeating variables and with the F.
Detailed Explanation
In dimensional analysis, we examine the relationships between physical quantities by considering their dimensions (like length, velocity, and force). The term 'theorem' here indicates that there are established rules for how these dimensions relate. Three specific variables—length, velocity, and force—are mentioned as important in this context. They form the repeating variables in the analysis, which are used to create dimensionless groups.
Examples & Analogies
Think of a chef who is using different ingredients (length, velocity, viscosity) to bake a cake. The cake recipe (the dimensional analysis) allows the chef to know how to mix these items in proportion to achieve the perfect texture without needing to know the specific details of each ingredient's chemistry.
Understanding Non-Dimensional Forms
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Similar way the length velocity will be the repeating variability and then I substituting the power experiment could be there to make a non-dimensional form of length, velocity density and the dynamic viscosity to make a will be non-dimensional.
Detailed Explanation
In this step, the focus is on converting the interdependent variables of length, velocity, density, and dynamic viscosity into non-dimensional forms. This involves understanding how to express these physical quantities in a way that their relationships do not depend on the specific units involved, allowing for generalized results.
Examples & Analogies
Consider making a fruit smoothie. Each ingredient like bananas, yogurt, and milk has a specific measure (like length or speed). However, you might want to express the recipe in a way that anyone can recreate it regardless of their measuring cups. This is similar to making the recipe (or relationship) non-dimensional—it's the same taste without depending on the particular size of the measuring tools.
Identifying Key Variables in Fluid Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now i can see the show you figures I do believe it these figures will talk many things what I may not express with these so-called limited times time-space. If you look at the things what it happens that when we have fluid flows in different force acts and the different force dominate at different conditions and when you do the fluid flow problems, we should point out which one is dominated.
Detailed Explanation
Here, the text explains that in fluid flow problems, we need to analyze the different forces at play and determine which one has the greatest impact under each condition. This is crucial for accurate prediction and analysis of fluid behavior in various scenarios.
Examples & Analogies
Imagine trying to redesign a roller coaster. Depending on how steep the hill is or how fast the train is moving (the forces acting on it), you need to consider which force (like gravity vs air resistance) is the most significant to ensure a safe and thrilling ride. Just like in fluid mechanics, understanding which force dominates helps make better designs.
Forces in Fluid Mechanics: Reynolds and Froude Numbers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
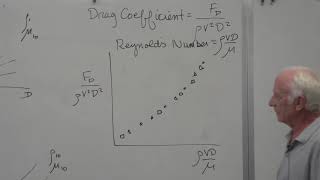
These are what? These are 2 forces are dominated here one is inertia forces the momentum blocks and another easy viscous component. These 2 forces are dominant and those 2 forces the ratio is Reynolds number. You can compute this...
Detailed Explanation
The discussion about Reynolds number indicates how fluid flow relates to inertia and viscous forces. The Reynolds number is a key dimensionless quantity that helps predict flow patterns in different fluid scenarios. A higher Reynolds number indicates turbulence, while a lower value suggests laminar flow.
Examples & Analogies
Think of it like comparing the flow of water through a garden hose (low Reynolds number, smooth flow) versus a wide, fast river (high Reynolds number, turbulent flow). The way water behaves in these two situations is crucial for determining how to manage fluid flow in engineering applications.
Other Dimensionless Numbers: Weber and Euler Numbers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look at other 2 numbers we not many times we use it but nowadays the level of the fluid mechanics problems what we are solving it we look at these formulas. One is called where the surface tension dominancy is there...
Detailed Explanation
Weber and Euler numbers are introduced as additional dimensionless groups important in analyzing fluid behavior. The Weber number reflects the influence of surface tension on fluid dynamics, while the Euler number relates pressure changes to inertial forces. These numbers help extend our understanding of fluid flow to situations where surface tension and cavitation are significant.
Examples & Analogies
When looking at bubbles in water, the Weber number helps us understand how surface tension affects their stability and formation. If you blow a bubble, you see that surface tension must be strong enough to hold it together against the forces trying to burst it where pressure changes can lead to interesting phenomena such as cavitation—like bubbles collapsing violently in a waterfall.
Conclusion and Application of Dimensional Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
That is what the dimensional analysis would not do for fluid mechanics any experiment we do these dimensional analysis to know the relationship between dependant variables and the independent variable in terms of dimensionless formats.
Detailed Explanation
The conclusion emphasizes the overall purpose of dimensional analysis in fluid mechanics: to establish relationships between interacting physical variables by transforming them into dimensionless groups. This essential practice aids in simplifying complex fluid dynamics problems and improving our understanding of fluid behaviors.
Examples & Analogies
Think of a recipe again. By converting the recipe to a general format (dimensionless), one can cook an entire meal (solve a problem) without being restricted to specific ingredients or measurements. Dimensional analysis does just that for fluid dynamics—letting scientists apply their findings broadly.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Dimensional Analysis: The process of using physical dimensions to analyze relationships between variables.
-
Reynolds Number: Ratio helping to distinguish flow regimes, vital in fluid dynamics.
-
Froude Number: Critical in free-surface flow scenarios, comparing inertia to gravity.
-
Weber Number: Important for analyzing droplet behavior and surface effects.
-
Euler Number: Relates pressure changes to inertial forces.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of Reynolds number applied in blood flow within arteries.
-
Froude number applied in analyzing water flow over spillways.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Reynolds flows so neat, low for laminar, high for turbulent beats.
🎯 Super Acronyms
F.G.I. for Froude
- F: = Inertia
- G: = Gravity
- I: = Important in flow.
🧠 Other Memory Gems
-
Remember 'R F W E' for Reynolds, Froude, Weber, and Euler when analyzing flow.
📖 Fascinating Stories
-
Imagine a race between gravity and inertia; the Froude number determines the winner based on flow conditions.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Dimensional Analysis
Definition:
A mathematical technique used to relate different physical quantities by their dimensions.
-
Term: Reynolds Number
Definition:
A dimensionless number that compares inertial forces to viscous forces in fluid flow.
-
Term: Froude Number
Definition:
A dimensionless number that compares inertial forces to gravitational forces, indicating flow regimes.
-
Term: Weber Number
Definition:
A dimensionless number that compares inertial forces to surface tension within a fluid.
-
Term: Euler Number
Definition:
A dimensionless number that compares pressure forces to inertial forces in a fluid flow.
-
Term: Dimensional Homogeneity
Definition:
The property of an equation where all terms have the same dimensions.
-
Term: Surface Tension
Definition:
The elastic tendency of liquids that makes them acquire the least surface area, influencing fluid behavior.