Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Dimensionless Forms
Unlock Audio Lesson
Welcome everyone! Today, we're diving into dimensionless forms, which are crucial in fluid mechanics. Can anyone explain why we might want to use dimensionless forms?
I think it's because it makes things easier to compare across different systems.
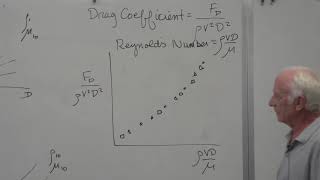
Exactly right! Dimensionless forms help us generalize principles across different fluid systems without focusing on the specifics of each one. One common example is the Reynolds number, which relates inertial forces to viscous forces.
How do we come up with the value of the Reynolds number?
Good question! It's calculated as the ratio of inertia to viscous forces. Remember, a higher Reynolds number indicates turbulent flow. Can we summarize this concept with an acronym?
Maybe we can use 'R' for Reynolds? Like, 'R' is for ratio of forces?
Great idea! 'R' for Reynolds. Let's keep that in mind as we move forward.
Key Variables in Fluid Flow
Unlock Audio Lesson
Now, let's look into the key variables: length, velocity, viscosity, density, and pressure. Who can tell me how these variables interact in fluid flow?
They probably influence each other, right? Like, changing the viscosity could change how fast a fluid flows.
Exactly! These fundamental variables work together in complex ways. For instance, if you change the viscosity, it can indeed affect the fluid's velocity and behavior.
Are there any dimensionless groups we derive from these variables?
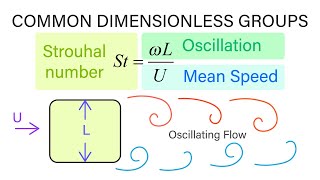
Yes! Using these variables, we can form several dimensionless groups like the Froude number, which compares inertia to gravity. This helps understand how gravitational effects might dominate in certain flow conditions.
And is that related to wave patterns?
Precisely! The Froude number is particularly important in scenarios involving waves, like in rivers or spills.
Practical Application of Dimensionless Forms
Unlock Audio Lesson
Let's discuss how dimensionless forms simplify our problems in fluid dynamics. Can anyone think of a complex problem that might become easier?
I imagine problems with varying fluid flows, like rivers, would be easier once we apply these forms.
Absolutely! By using dimensionless forms, we can predict flow patterns and behavior without getting bogged down by varying units and scales. What about another example?
Maybe when designing airplanes, we use these forms to ensure stability across different speeds?
That's correct! Engineers apply these principles to design safe and efficient aircraft that can maintain performance across various conditions. What’s a common non-dimensional form associated with such applications?
The Mach number, which compares flow speed to the speed of sound!
That's right! Keeping in mind these essential concepts sets the stage for deeper studies in fluid mechanics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section outlines the foundation of using dimensionless forms in fluid dynamics, explaining the significance of variables like length, velocity, viscosity, and how they relate to dimensionless numbers such as Reynolds number, Froude number, Weber number, and others. It highlights their role in simplifying fluid flow problems.
Detailed
Introduction to Dimensionless Forms
This section emphasizes the necessity of utilizing dimensionless forms in fluid mechanics, allowing complex fluid dynamics problems to be analyzed more effectively. It begins by introducing the fundamental variables in fluid flow, namely length, velocity, viscosity, density, and pressure. The repetitive nature of these variables leads to a derived understanding of their interactions through dimensionless numbers.
Key players in this discussion are various dimensionless numbers:
- Reynolds Number: This number is crucial in determining flow patterns; it relates inertial forces to viscous forces, indicating whether the flow is laminar or turbulent.
- Froude Number: This relates inertial forces to gravitational forces, affecting flow behavior near free surfaces.
- Weber Number and Euler Number: These capture the effects of surface tension and pressure changes, respectively, making them essential in scenarios involving fluid interfaces.
The section illustrates that by grouping variables appropriately, one can develop dimensionless forms that simplify modeling and computational analysis, enhancing the understanding of fluid effects under varying conditions. Ultimately, mastering dimensionless analysis aids in predicting fluid behavior across scales and applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Dimensionless Forms
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Dimensionless forms are important in fluid mechanics. They allow us to simplify complex relationships between physical quantities such as length, velocity, and viscosity into groups without physical units.
Detailed Explanation
Dimensionless forms help in comparing different systems by removing the units from the equations. For instance, when we use dimensionless variables, we can analyze the fluid flow based on ratios, like the Reynolds number, which characterizes the flow regime without the need for specific dimensional analysis for each case.
Examples & Analogies
Think of dimensionless forms like a recipe scaled for several servings. The actual amount of ingredients (like length and pressure) varies, but the ratio of ingredients (dimensionless numbers) remains the same. This allows anyone to understand the cooking process regardless of kitchen sizes.
The Role of Repeating Variables
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Repeating variables are essential in establishing dimensionless forms. In fluid mechanics, we typically consider length, velocity, and viscosity as repeating variables when creating dimensionless groups.
Detailed Explanation
Repeating variables are quantities that we can vary in our experiments, while still allowing us to analyze results without dimensionality. By expressing all variables in terms of these repeating variables, we generate dimensionless groups that simplify our equations. For example, using the length (L), velocity (V), and viscosity (μ) enables us to construct important dimensionless groups such as the Reynolds number.
Examples & Analogies
Imagine a team working on a group project where everyone has a specific task (length, velocity, viscosity). By coordinating these tasks (repeating variables), the team creates a smooth flow of work (dimensionless form) that leads to successful project completion without confusion about individual responsibilities (dimensionality).
Key Dimensionless Numbers
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In fluid mechanics, several key dimensionless numbers are significant: the Reynolds number, Froude number, Weber number, and Euler number. Each of these numbers relates different forces acting on a fluid.
Detailed Explanation
Dimensionless numbers represent relationships between different fluid properties. For instance, the Reynolds number helps us determine whether the flow is laminar or turbulent by comparing inertial forces to viscous forces. The Froude number compares inertial forces to gravitational forces, providing insights into fluid behavior under gravitational effects. Similar roles are played by the Weber and Euler numbers concerning surface tension and pressure drop effects, respectively.
Examples & Analogies
These dimensionless numbers can be likened to performance metrics in sports. Just as an athlete's performance is often measured by ratios, like time per distance run (speed), fluid mechanics uses ratios to understand the behavior of flows under various conditions, allowing engineers and scientists to 'optimize' designs for efficiency.
Application of Dimensionless Forms
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
By applying dimensionless forms, we can predict behavior in complex fluid scenarios without conducting exhaustive experiments. This helps engineers design better systems and understand flow characteristics.
Detailed Explanation
Using dimensionless forms allows engineers to simulate and predict fluid behavior across different systems without needing to treat each scenario uniquely. By comprehending how dimensionless groups interact, we can apply knowledge from one system to predict behavior in another, aiding in everything from aircraft design to understanding natural waterways.
Examples & Analogies
It's similar to understanding game strategies in different sports. A coach who recognizes patterns in gameplay can apply similar tactics across various sports disciplines, achieving success without reinventing strategies for each game. Similarly, engineers can apply dimensionless concepts learned from one type of fluid flow to inform analyses of other flows.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Dimensionless Forms: Important for simplifying fluid mechanics problems and comparing different systems.
-
Reynolds Number: Measures the ratio of inertial forces to viscous forces, indicating flow behavior.
-
Froude Number: Helps understand gravitational influences and wave patterns in fluid flows.
-
Weber Number: Represents the effect of surface tension compared to inertial forces.
-
Euler Number: Indicates the relationship between pressure forces and fluid inertia.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
To calculate the Reynolds number for a fluid, plug the velocity, density, and viscosity into the formula: Re = (Density * Velocity * Length) / Viscosity and interpret it to determine if the flow is laminar or turbulent.
-
In a spillway design, engineers might use Froude number to assess how water behaves over the spillway, leading to safe and effective design strategies.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In flows that twist and turn, Reynolds number's what you learn, high for turbulence, low for calm, keep it handy as your balm.
📖 Fascinating Stories
-
Imagine two rivers: one calm and the other rushing. The calm river is all about peace (low Reynolds number), while the rushing one is wild and turbulent (high Reynolds number). They both show us how flows can differ greatly!
🧠 Other Memory Gems
-
Remember 'FREWE' - Froude for waves, Reynolds for flow, Euler for pressure, Weber for surface tension. This will keep the dimensionless numbers straight!
🎯 Super Acronyms
MEMORIZE
- M: for Mach
- E: for Euler
- R: for Reynolds
- F: for Froude
- and W for Weber - these leads to fluid mechanics success!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Dimensionless Form
Definition:
A mathematical representation that does not have physical units, allowing for easier comparison and analysis.
-
Term: Reynolds Number
Definition:
A dimensionless quantity used to predict flow patterns in different fluid flow situations, defined as the ratio of inertial forces to viscous forces.
-
Term: Froude Number
Definition:
A dimensionless number that compares inertia to gravitational forces in fluid flows, significant in understanding wave motion.
-
Term: Weber Number
Definition:
A dimensionless number that describes the relative importance of inertial forces to surface tension forces in a fluid.
-
Term: Euler Number
Definition:
A dimensionless number that expresses the ratio of pressure forces to inertial forces in a fluid flow.