Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fluid Mechanics and Bernoulli's Equation
Unlock Audio Lesson
Good afternoon everyone! Today, we'll explore the fascinating world of fluid mechanics, starting with Bernoulli's equation. Can anyone tell me what Bernoulli's equation relates?
It relates pressure, velocity, and height of fluid?
Exactly! The equation illustrates the conservation of energy in fluid flow. We can think of it as: 'Pressure + Kinetic Energy + Potential Energy = Constant.' Who can remind us what this means physically?
It means that as fluid speeds up, the pressure decreases!
That's right! This principle is vital when considering the effects of hurricanes or cyclones on buildings. Now, can you think of another context where we apply this equation?
Maybe in piping systems or water flow control?
Correct! Great job! Remember, Bernoulli's equation helps us solve practical problems in numerous fields, especially in civil engineering.
Mass Conservation Principles
Unlock Audio Lesson
Next, let's dive into mass conservation. What can you tell me about the mass conservation equation?
It says that mass inflow must equal mass outflow in a steady flow?
Exactly! This is crucial for analyzing fluid systems. Can anyone explain how we mathematically express this idea?
You can express it as Q1 = Q2, where Q is the volumetric flow rate!
Great! Q1 and Q2 represent flow rates at different points. Understanding these relationships aids in simplifying complex scenarios.
What happens if the velocities change?
Good question! If velocity changes, the cross-sectional area must also change to keep Q constant. This leads us to the concept of continuity. Remember the acronym A1V1 = A2V2—it sums it up!
Applying Bernoulli's Equation
Unlock Audio Lesson
Now that we've covered the principles, let's apply Bernoulli's equation with a real-world example. Can anyone suggest a situation?
Wind load on a building during a cyclone!
Exactly! If a cyclone generates wind speeds of 250 km/h, how do we determine the pressure difference across the building?
We can use the Bernoulli equation to calculate that!
Correct again! The pressure outside decreases as the wind speed increases, which leads to potential uplift on structures like roofs. This example perfectly illustrates the real-world importance of fluid mechanics.
Are there assumptions we need to keep in mind when using Bernoulli's equation?
Yes! It assumes steady, incompressible, and non-viscous flow. Remembering these helps refine our calculations.
Momentum Conservation in Fluid Mechanics
Unlock Audio Lesson
Finally, let’s address momentum conservation. How is it different from mass conservation?
Momentum considers the mass flow rate multiplied by velocity?
Precisely! Hence the expression: F = Δ(mv)/Δt. What implications does this have in fluid dynamics?
It can help determine forces exerted by fluids, right?
Exactly! Understanding these forces is key when evaluating structures like pipes or tanks under various flow conditions.
What kind of examples can we see in real life?
Good question! Consider water jets in hydraulic machines or aircraft wings generating lift. Each applies these principles to efficiently manipulate fluids.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section introduces basic fluid mechanics equations, emphasizing Bernoulli's equation and its applications, particularly in assessing wind loads on structures and understanding fluid flow in various contexts. It details the principles of mass and momentum conservation to facilitate problem-solving in fluid mechanics.
Detailed
In fluid mechanics, fundamental equations play a crucial role in analyzing fluid behaviors and structures under various forces. This section elaborates on these expressions, particularly Bernoulli's equation, which articulates the relationship between pressure, velocity, and elevation in fluid flow. Through real-life examples, such as estimating wind impact on structures during cyclones, the relevance of these equations becomes evident. The section further establishes mass and momentum conservation principles, outlining necessary assumptions (like steady and one-dimensional flow) to simplify complex problems into manageable equations. These foundational equations enable engineers to calculate parameters like lift forces and fluid velocities effectively.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Mass Conservation Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
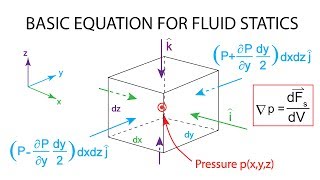
Like if you look it that these mass conservation equations which are very basic equations. If you look any control volume, we have considered is that this is a change in the mass flow rates. And this is mass out flux, influx. That is what is should equal to zero. This is what the mass conservation equations.
Detailed Explanation
The mass conservation equation states that in any control volume, the mass inflow must equal the mass outflow in a steady state. This means whatever mass enters a control volume must leave it, leading to no accumulation of mass within the system, resulting in the equation: inflow - outflow = 0. If we simplify this, we can express it as Q1 = Q2, indicating that the flow rate at entry and exit of a control volume remains consistent.
Examples & Analogies
Imagine a water tank. If water flows in through a pipe at a certain rate and must simultaneously flow out through another pipe, the flow rates must balance for the tank to remain at a constant level. If more water flows in than out, the tank will fill up; if more flows out than in, it will empty.
Momentum Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Similar way if you look at this momentum equations what we derived earlier and that what will be expressions like this. So what you supposed to do it whenever write these type of big equations, try to write this all these dimensions and check it the dimensions of each components whether they are equal.
Detailed Explanation
The momentum equation in fluid mechanics relates the momentum of a fluid parcel to the forces acting on it. It's vital to ensure units are consistent when formulating these equations; thus, checking dimensions ensures that each term is compatible. The momentum equation can show how fluids respond when forces are applied, crucial for applications like flow in ducts or around objects.
Examples & Analogies
Think of a soccer ball being kicked. The amount of force applied to the ball (momentum change) depends on how hard it is kicked (effect of force). Just like in fluid mechanics, understanding how much force changes an object's momentum helps predict where the ball will go.
Bernoulli’s Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
And if you look it that basic equations of Bernoulli’s equations which has the pressure head component, the velocity head component and the elevations head those what if you include it as the flow energy for weight, the kinetic energy for weight and the potential energy for weight.
Detailed Explanation
Bernoulli’s equation describes the behavior of a flowing fluid and is derived from the conservation of energy principle. It states that an increase in the fluid's velocity corresponds to a decrease in pressure or potential energy. The equation can be represented as P + (1/2)ρv² + ρgh = constant, where P is the pressure energy, ρv² is the kinetic energy per unit volume, and gh is the potential energy per unit volume. It shows how different forms of energy interchange in fluid flow.
Examples & Analogies
Imagine water flowing through a garden hose. When you place your thumb over the end, you reduce the outlet area; the water speeds up as it exits (higher velocity). Consequently, the pressure in the hose decreases because the energy of the fluid has transformed from pressure energy to kinetic energy.
Application of Bernoulli’s Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
And if you look at this way, it is quite easy to compute the wind load estimations, but we should know exactly how to apply the Bernoulli’s equations and what are the assumptions are there.
Detailed Explanation
To effectively use Bernoulli’s equation, it’s important to understand its assumptions: the flow must be steady, incompressible, and frictionless. When analyzing real-world problems, such as estimating wind loads on structures during storms, Bernoulli's can predict how pressure differs at various points in the flow, allowing engineers to calculate forces acting on objects.
Examples & Analogies
Consider a plane's wing. When the plane moves, air flows faster over the top of the wing and slower underneath, creating lower pressure above and higher pressure beneath. This pressure difference generates lift, demonstrating Bernoulli's principle in action.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Bernoulli's Principle: Relates the conservation of energy in flowing fluids, indicating pressure and velocity interrelation.
-
Mass Conservation: A foundational concept ensuring mass inflow equals mass outflow in steady flow conditions.
-
Momentum Conservation: Dictates that momentum is conserved in a fluid system without external forces.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Estimating wind loads on structures such as buildings during cyclones using Bernoulli's principle.
-
Calculation of water flow velocities through varying diameter pipes using mass conservation principles.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a fluid that flows, pressure and speed both shows; as one rises high, the other must sigh.
📖 Fascinating Stories
-
Imagine a river, where the flow speeds up as it narrows. Trees get uprooted if the speed is too quick, just like how pressure drops when velocity peaks.
🧠 Other Memory Gems
-
Remember P = 0.5ρv² + ρgh as 'Pressure minus kinetic and gravitational adds up to none'.
🎯 Super Acronyms
VAP – Velocity, Area, Pressure; remember, when one goes up, the others react!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Bernoulli's Equation
Definition:
An equation that describes the conservation of energy in a flowing fluid, relating pressure, velocity, and height.
-
Term: Mass Conservation
Definition:
A principle stating that mass cannot be created or destroyed, leading to the equation Q1 = Q2 in fluid flow.
-
Term: Momentum Conservation
Definition:
A principle stating that the momentum of a fluid system is conserved in the absence of external forces.
-
Term: Flow Rate (Q)
Definition:
The volume of fluid flowing per unit time, commonly expressed in m³/s.
-
Term: Control Volume
Definition:
A defined region in space where the analysis of fluid flow and properties is conducted.