Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Momentum Equations
Unlock Audio Lesson
Today, we will delve into momentum equations in fluid mechanics. Momentum, as you know, is the product of mass and velocity. Can anyone explain why it’s important to consider momentum in fluid flows?
It's important because fluids exert forces when they move, especially when interacting with objects.
Exactly! When fluids flow past surfaces, they can exert forces that are critical for design and analysis. What do we call the principle that relates mass inflow and outflow in a control volume?
It's the conservation of mass!
Correct! Remember the acronym 'MASS FLOW' to help you recall the steps in conservation principles: **M**ass **A**ccounting **S**tudy **S**teady condition **F**lux **L**imits **O**utflow **W**elter. Alright, let's move on.
Applying Momentum Equations
Unlock Audio Lesson
Now, let’s discuss how to apply these momentum equations. Can anyone tell me the general linear momentum equation for fluids?
Is it something like the change in momentum equals the sum of forces?
"Exactly! It's represented mathematically as:
Bernoulli's Equation
Unlock Audio Lesson
Now let's connect momentum equations to Bernoulli's equation. What does Bernoulli's equation represent?
It represents the conservation of energy for flowing fluids!
Yes! It combines pressure energy, kinetic energy, and potential energy in a flowing streamline. Can anyone remember those components?
P + ½ρv² + ρgh = constant!
Spot on! And how does this help us in real-life scenarios, like the ones we've seen earlier?
It helps us estimate forces on structures caused by fluid movement!
Exactly! Applying Bernoulli's principle allows us to predict and mitigate effects in engineering designs. Before we finish, can anyone explain why Bernoulli’s assumptions matter?
Because they define the conditions under which the equations are valid, like incompressible and non-viscous flow?
Great summarization! Always remember the key assumptions of Bernoulli's equation: ***INVIS*** - Incompressible, Non-viscous, Ideal fluid, Steady flow. Alright!
Real-World Applications
Unlock Audio Lesson
Let’s examine how momentum equations apply to real-world engineering problems. How about estimating wind loads on buildings?
We would need to determine the pressure difference caused by the wind speed!
Exactly! And by using Bernoulli’s equation, we can estimate those pressures. Imagine wind speeds during a cyclone; what pressure would be significant?
Higher wind speeds lead to increased uplift forces on building roofs!
Good! So we would calculate pressure at the wind speed measured and ascertain safety factors in structure designs. Let's consider another example...
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section delves into the concept of momentum equations within the realm of fluid mechanics, emphasizing the application of mass conservation principles and the derivation and relevance of Bernoulli's equations. It highlights the relationship between pressure, velocity, and elevation, crucial for estimating forces and analyzing fluid flow scenarios in engineering contexts.
Detailed
Momentum Equations
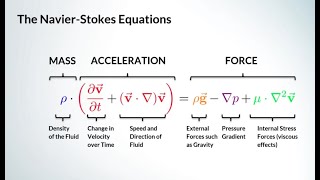
In fluid mechanics, momentum equations play a vital role in understanding the behavior of fluid flows around bodies and within systems. Momentum, defined as the product of mass and velocity, is conserved in fluid flows, and this principle leads to the formulation of momentum equations. The section begins by reiterating the conservation of mass, presenting how mass inflows and outflows in a control volume can be quantified using mass conservation equations.
The momentum equations are crucial when analyzing fluid interactions with structures, as they help calculate forces exerted by fluid flows. This section focuses on the linear momentum equation, which results from applying Newton's second law to fluid motion. Additionally, Bernoulli’s equation is introduced as a method for integrating pressure, velocity, and potential energy terms, providing insights into the energetic relationship of fluids in motion.
Real-world applications are also considered, such as the estimation of wind loads on buildings and the impact of cyclonic forces on structures, showcasing the importance of momentum calculations in civil engineering. By establishing relationships between pressure gradients and flow velocities, practitioners can predict and mitigate risks in engineering design.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Momentum Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
And if you look at this momentum equations what we derived earlier and that what will be expressions like this. So what you supposed to do it whenever write these type of big equations, try to write this all these dimensions and check it the dimensions of each components whether they are the equal.
Detailed Explanation
Momentum equations are derived from fundamental principles of fluid mechanics. They describe how the momentum of fluid changes as it flows through a control volume. In practical applications, it is essential to ensure that the dimensions of each component in the equation are consistent; this is termed 'dimensional analysis.' For example, if you have an equation that expresses force, you need to confirm that all components involved contribute consistently to this force unit (Newtons in SI).
Examples & Analogies
Imagine measuring how fast you can push a car down a hill. You need to consider how heavy the car is (mass), how steep the hill is (angle), and how much force you can exert. If your measurements are not consistent, like mixing pounds with kilograms, the results won't make sense. Similarly, in momentum equations, every term must align dimensionally.
Linear Momentum Relation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Linear momentum relation in the stream wise direction.
Detailed Explanation
The linear momentum relation defines the change in momentum for a unit mass over time due to external forces applied in the direction of fluid flow. It highlights how the velocity of the fluid changes along the streamline, influenced by factors such as pressure and friction. When analyzing flow, it's crucial to account for all forces acting on the fluid, which can significantly affect its momentum.
Examples & Analogies
Think about riding a bike downhill. As you go down, gravity pulls the bike faster, and the momentum increases. If there's a strong wind (a force acting against you), it slows down your speed. This scenario represents how different forces interact to change momentum in fluid systems.
Bernoulli’s Equation Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
And if you look at that basic equations of Bernoulli’s equations which has the pressure head component, the velocity head component and the elevations head those what if you include it as the flow energy for weight, the kinetic energy for weight and the potential energy for weight.
Detailed Explanation
Bernoulli’s equation captures the conservation of energy in a moving fluid, outlining how pressure head, velocity head, and elevation head are interconnected along a streamline. Pressure head corresponds to the stored energy due to fluid pressure, velocity head indicates kinetic energy due to fluid velocity, and elevation head represents potential energy due to gravitational height. Each of these components is crucial for understanding how fluids move and behave under different conditions.
Examples & Analogies
Consider a water slide at a water park. At the top of the slide, the water has maximum potential energy (height) and minimal kinetic energy (motion). As it slides down, this potential energy converts to kinetic energy, increasing the speed of the water. Bernoulli’s principles help explain this energy conversion through pressure, height, and velocity relationships.
Applications of Momentum Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us solve the five questions from GATE question set. The first examples one what I consider is the circular water pipes shown in the sketch are flowing full condition.
Detailed Explanation
Applying momentum equations through practical problems such as fluid flow in pipes offers insights into real-world situations. By setting up equations that equate inflow and outflow, one can calculate important quantities like flow rates and velocities. For example, if you know the diameter of pipes and the velocities at different sections, you can use mass conservation and momentum principles to find unknown speeds.
Examples & Analogies
Think of a water hose where you pinch one end. The pressure builds up, and when released, the water shoots out faster. By analyzing how water flows in the hose, we can predict how much pressure is needed or how fast the water will come out when comparing different hose diameters. These same principles apply to momentum equations in various engineering problems.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Momentum: The product of mass and velocity, crucial in fluid mechanics.
-
Bernoulli's Equation: A principle that relates pressure, velocity, and height in fluid flows.
-
Control Volume: A defined volume in space to apply conservation laws for mass and momentum.
-
Mass Flow Rate: The measure of the mass of fluid passing through a cross-section per unit time.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Estimating wind loads on buildings during cyclones using Bernoulli's equation.
-
Calculating forces exerted by fluid flows in pipes and tanks.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Momentum in flow, just go with the flow, mass times how fast, that's how we know!
📖 Fascinating Stories
-
Once in a kingdom where water flowed, a wise engineer used momentum to forebode, predicting the forces as rivers would grow, he calculated safely, to help us all know!
🧠 Other Memory Gems
-
Remember 'P-V-H' for Bernoulli: Pressure, Velocity, Height, constant for fluidity!
🎯 Super Acronyms
Use 'INVIS' to recall Bernoulli's assumptions
- Incompressible
- Non-viscous
- Ideal fluid
- Steady flow.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Momentum
Definition:
The product of mass and velocity of an object; an important quantity in fluid mechanics.
-
Term: Bernoulli’s Equation
Definition:
An equation that describes the conservation of energy in fluid flow, relating pressure, velocity, and height.
-
Term: Control Volume
Definition:
A specified region in space through which fluid can flow; used for applying conservation laws.
-
Term: Mass Flow Rate
Definition:
The mass of a substance passing through a surface per unit time.