Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Bernoulli’s Equation
Unlock Audio Lesson
Today we will dive into Bernoulli's Equation. Who can tell me what this equation relates?
It relates pressure, velocity, and elevation in a moving fluid?
Exactly! Now, does anyone know what assumptions must be made to apply Bernoulli's Equation effectively?
I think it requires steady flow?
Great point! Steady flow is one of the key assumptions. Another is incompressible flow. Does anyone know why that’s necessary?
Because the density of liquids is pretty much constant, unlike gases, right?
Absolutely! Remember this acronym: **SI** for Steady and Incompressible! Let's keep building on these ideas.
Friction and Non-viscous Flow Assumptions
Unlock Audio Lesson
Moving on, let’s talk about non-viscous flow. Anyone want to explain this assumption?
It means we ignore the frictional forces acting in the fluid?
Exactly! The assumption of non-viscous flow simplifies our calculations, as energy loss due to friction is not considered. How might this affect real-life scenarios?
In real situations, especially in pipes, we do have friction which needs to be accounted for?
Very true! This brings us to the limitations of Bernoulli’s equation in practical applications. My tip: always assess the significance of viscosity in fluids!
Streamlines and Flow Conditions
Unlock Audio Lesson
Lastly, let’s discuss streamlines. Why is it important that Bernoulli’s equation applies along a streamline?
Because the properties of the fluid are consistent along that path?
Correct! Along a streamline, the flow is smooth and continuous, allowing us to analyze it without sudden changes. Remember this concept; it’s integral to fluid dynamics. Can anyone illustrate a scenario where this assumption might break down?
Maybe in turbulence, where the flow breaks and becomes chaotic?
Excellent example! Turbulent flow indeed complicates applications of Bernoulli's equation. Remember: **ST** for Steady and Turbulent conditions. Great work today, everyone!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the assumptions behind Bernoulli’s equation, including steady flow, incompressible flow, and the effects of friction. Understanding these assumptions is crucial for correctly applying Bernoulli’s equation to real-world fluid dynamics problems.
Detailed
Detailed Summary
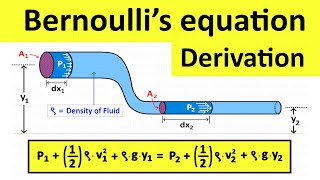
Bernoulli’s Equation is a fundamental principle in fluid mechanics used to describe the relationship between pressure, velocity, and height in a flowing fluid. However, specific assumptions must be satisfied for the equation to be applicable.
The primary assumptions include:
1. Steady Flow: The flow parameters (velocity, pressure, and height) at a given point in the fluid do not change over time.
2. Incompressible Flow: The fluid density remains constant, which is a valid assumption for liquids.
3. Non-viscous Flow: The effects of viscosity (friction) are negligible, which means there is no energy loss due to frictional forces.
4. Along a Streamline: Bernoulli’s equation applies along a streamline, implying that the flow can be considered as a series of parallel, uninterrupted layers.
These assumptions are vital as they allow simplifications that facilitate the analysis of fluid dynamics problems, making it easier to predict how fluids behave under various conditions.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Steady Flow Assumption
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The first assumption of Bernoulli's equation is that the flow must be steady. This means that the flow properties at a point do not change with time.
Detailed Explanation
In a steady flow, the velocity of the fluid at any particular point remains constant over time. This means that if you were to measure the flow properties like velocity, pressure, and elevation at a specific point in the fluid, those measurements would be the same each time you took them. This assumption simplifies calculations because it allows us to use constant values in the equations.
Examples & Analogies
Imagine a river flowing steadily. If you were to stand at a specific spot on the riverbank, the water depth, color, and speed of the water passing by would remain the same as long as no new water is added or removed. This is similar to steady flow in fluid mechanics.
Incompressible Flow Assumption
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Another important assumption is that the fluid is incompressible, meaning its density remains constant throughout the flow.
Detailed Explanation
In many fluid flow situations, especially with liquids like water, density does not change significantly regardless of the pressure or temperature changes. This assumption makes mathematical formulations simpler because we can treat the fluid density as a constant value during calculations and apply it across different sections of the flow.
Examples & Analogies
Think about filling a flexible balloon with water. No matter how much you squeeze it or move it around, the water inside will remain at a nearly constant density. Same thing for most water flow cases, which is why we consider it incompressible in many applications.
Irrotational Flow Assumption
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The flow is assumed to be irrotational, meaning that there is no rotation of fluid elements about their center of mass.
Detailed Explanation
Irrotational flow implies that the fluid moves in such a way that each small element of the fluid does not have any angular momentum about its center, simplifying the analysis. This leads to the conclusion that the potential energy in the flow can be considered uniformly distributed or dependent solely on height, reducing complexity in calculations.
Examples & Analogies
Picture a smoothly flowing river. If you dropped a leaf on the surface, it would move downstream without spinning or swirling around in place. This behavior illustrates irrotational flow where the elements of fluid are translating cohesively rather than rotating.
Negligible Viscosity Assumption
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The effects of viscosity are often neglected in ideal fluid flow conditions, implying that the fluid is non-viscous.
Detailed Explanation
Viscous effects occur due to friction between fluid layers; in ideal scenarios, these effects are minimal or ignored. This makes the equations easier to solve and the behavior of fluids more predictable, as real-world fluids often exhibit complex viscous behavior, particularly in turbulent conditions.
Examples & Analogies
Consider the difference between water and honey. In water, you can imagine fluid layers flowing over one another smoothly with little resistance, leading to less complicating effects and allowing us to use the Bernoulli equation. Honey, however, exhibits strong viscous forces that complicate flow and would not be modeled well by Bernoulli’s equation.
No Energy Loss Assumption
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Bernoulli’s equation assumes that there are no energy losses due to friction, turbulence, or other dissipative factors.
Detailed Explanation
This assumption means that all the energy in the fluid system is conserved and can be transformed from pressure energy to kinetic or potential energy without any losses. While this is not true in all real cases, it provides a good approximation in many idealized scenarios, allowing engineers to predict fluid behavior with reasonable accuracy.
Examples & Analogies
Imagine a perfectly smooth water slide where you slide down without any slowing down due to friction. You start with gravitational potential energy at the top which transforms completely into kinetic energy at the bottom. In the real world, slides will have some friction, slowing you down, but in our idealized scenario, we consider it frictionless.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Steady Flow: A flow condition where properties do not change over time.
-
Incompressible Flow: Assumes fluid density remains constant, essential for liquids.
-
Non-viscous Flow: Assumes negligible effects from viscosity, simplifying calculations.
-
Streamline: The path fluid particles follow in a flow, crucial for applying Bernoulli's equation.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Estimating wind loads on a building during a cyclone, applying Bernoulli’s equation to understand pressure differentials.
-
Fluid flowing through a pipe with varying diameters requires using Bernoulli’s equation under applicable assumptions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For flow that is steady, keep viscosity heavy!
📖 Fascinating Stories
-
Imagine a serene river flowing steadily, with fish gliding through smooth waters—this is the essence of steady and incompressible flow!
🧠 Other Memory Gems
-
Remember SINC for Bernoulli's assumptions: Steady, Incompressible, Non-viscous, along a Streamline.
🎯 Super Acronyms
Use the acronym **STIN** to remember
- Steady
- Turbulent
- Incompressible
- Non-viscous.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Steady Flow
Definition:
A flow condition where fluid parameters at a specific point do not change over time.
-
Term: Incompressible Flow
Definition:
A flow assumption where fluid density remains constant, typically valid for liquids.
-
Term: Nonviscous Flow
Definition:
A flow condition in which frictional effects (viscosity) are ignored.
-
Term: Streamline
Definition:
A trajectory of fluid particles, which helps illustrate the flow path in fluid mechanics.