Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Steady Flow
Unlock Audio Lesson
Today, we’re discussing steady flow. Can anyone tell me what steady flow means?
I think it means the flow parameters like velocity do not change over time?
Exactly! In steady flow, conditions like velocity and pressure at any point in the fluid remain constant over time. This concept allows us to simplify our calculations.
What about if we have different flows at different points? How does that work in steady flow?
Good question! While conditions are constant at a point, they can vary from one location to another. We can analyze these changes using Bernoulli’s equation across different points.
So, we're using the same principle even if the velocities differ?
Correct! The energy balance allows us to compare velocities and pressures across points in the flow.
Bernoulli's Equation in Steady Flow
Unlock Audio Lesson
Let’s apply Bernoulli's equation. Can someone state what it includes?
It includes pressure, kinetic energy, and potential energy per unit weight of fluids.
Exactly! It relates how pressure, velocity, and height interact. The equation is often expressed as the sum of these components being equal along a stream line.
And we use it for practical problems, right? Like assessing wind loads on buildings?
Yes! For example, during a cyclone, we can use Bernoulli’s equation to calculate pressure differences and the impact on structures.
So, the pressure differential is what causes the roof to lift?
Exactly! Conceptually, if we understand how these components interact, we can predict and design structures to withstand such forces.
Mass and Momentum Conservation Principles
Unlock Audio Lesson
Now, let’s shift to mass and momentum conservation. Who can explain what the conservation of mass implies?
It implies that mass inflow equals outflow for steady states.
Correct! This principle simplifies our calculations when analyzing fluid systems. Now, what about momentum?
Momentum conservation applies when a force acts on a fluid, changing its motion?
Exactly! We analyze forces within control volumes to see how momentum is conserved despite external influences.
Like in a pipe bend where the flow direction changes, right?
Exactly! The change results in pressure differences and forces that we need to account for.
Practical Applications of Steady Flow
Unlock Audio Lesson
Let’s go through a real-world problem. Can anyone think of a situation where we apply these concepts?
Estimating wind loads on buildings based on cyclonic winds?
Very good! The calculations involve determining pressure differences using Bernoulli's equation to ensure buildings can withstand such forces.
What data do we need for those calculations?
You will need the wind speed, building dimensions, and height to find pressures and forces from the wind.
And we then apply the mass and momentum equations to support our designs?
Absolutely! All these aspects combine to ensure safe and efficient engineering designs.
Conclusion and Recap
Unlock Audio Lesson
So, to summarize, what have we learned about steady flow today?
Steady flow means no changes at a point over time, and we analyze it using Bernoulli's equation.
We also talked about conservation of mass and momentum in control volumes.
Correct! And these principles allow us to perform practical calculations, such as assessing forces due to wind loads on structures. Remember to always analyze the flow conditions before applying equations.
Thanks! I feel more confident about using these equations for engineering designs.
Me too! I appreciate how everything ties together.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In the study of fluid mechanics, this section focuses on steady flow, key equations including Bernoulli's equation, and practical applications like wind load estimation on buildings. It illustrates problem-solving techniques involving control volumes and flow classifications, particularly in civil engineering scenarios.
Detailed
Steady Flow
In fluid mechanics, the concept of steady flow is essential in analyzing how fluids move through systems, particularly in engineering applications. This section delves into the notation and formulation of key principles such as Bernoulli's equation, conservation of mass, and momentum equations, all crucial in modeling steady flow scenarios.
Key Aspects Covered:
- Real-Life Applications: The discussion starts with practical contexts, such as estimating wind loads on structures during cyclonic conditions. The calculations leverage Bernoulli’s equation under steady-flow assumptions to predict pressure differences caused by external forces like wind.
- Control Volume Concept: Understanding flow through control volumes is introduced, stating that the mass inflow equals outflow at a steady state. This principle assists in simplifying complex flow scenarios into manageable calculations.
- Basic Equations: The section reiterates three primary equations fundamental to fluid mechanics:
- Conservation of Mass: Expressed as mass inflow equals mass outflow for steady-state conditions, indicating that the system does not accumulate or deplete mass over time.
- Momentum Equations: These equations capture the relationship between velocity, force, and momentum change in a fluid's trajectory.
- Bernoulli’s Equation: It describes the balance between pressure, kinetic energy, and potential energy along a streamline, demonstrating that these quantities remain constant when the flow is steady and frictionless.
The significance of these principles is not only theoretical but also extends to practical engineering applications, emphasizing their vital role in various fields, particularly civil engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Steady Flow Concept
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
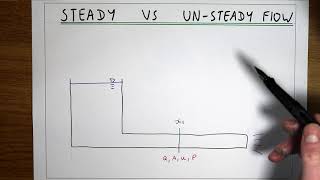
Flow is considered steady if the fluid properties at any given point do not change over time.
Detailed Explanation
In fluid mechanics, 'steady flow' means that conditions like speed, pressure, and density at any point in a fluid system remain constant over time. This implies that if you were to measure these properties at a specific location, your readings would not fluctuate as time passes.
Examples & Analogies
Imagine a river flowing steadily. If you stand at a particular spot and take measurements of the water's speed and temperature, those readings will be consistent as long as the flow conditions remain the same. This is similar to observing traffic on a highway where the cars move at a constant speed without stops.
Mass Conservation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In steady flow, the mass inflow is equal to the mass outflow, leading to the conservation of mass principle.
Detailed Explanation
The principle of mass conservation states that in a steady flow situation, the amount of mass entering a control volume must equal the amount of mass leaving that volume, plus any change in mass stored within it. For example, if you have water flowing through a pipe, the same volume of water that comes in from one side must go out the other side in a given time period, assuming there is no accumulation.
Examples & Analogies
Think of a water balance in a bathtub with the tap running. If water flows into the tub at the same rate that you are draining it, the water level stays constant. If you close the drain, the level rises, but while it’s steady, the flow in equals the flow out.
Bernoulli’s Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Bernoulli’s equation relates the pressure, velocity, and elevation of a fluid in steady flow.
Detailed Explanation
Bernoulli's equation is a fundamental equation in fluid dynamics, expressing the principle of conservation of energy for flowing fluids. It states that the total mechanical energy along a streamline (comprising pressure energy, kinetic energy, and potential energy) remains constant. Thus, if the velocity of the fluid increases, the pressure must drop, and vice versa, as long as the flow is steady.
Examples & Analogies
Consider a garden hose: when you put your thumb over the end, the water shoots out faster because you’re reducing the cross-sectional area. As the speed increases, the pressure at that point drops, demonstrating Bernoulli’s principle as energy is conserved.
Flow Classification
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Flow can be classified into various types, including steady, unsteady, uniform, and non-uniform flows.
Detailed Explanation
In fluid mechanics, different flow types help to analyze and predict fluid behavior. 'Steady flow' means properties do not change with time, while 'unsteady flow' means they do. 'Uniform flow' indicates properties such as velocity are constant across the flow area, while 'non-uniform flow' denotes variations. Understanding these classifications aids engineers in designing systems involving fluids.
Examples & Analogies
Imagine a person running at a constant speed—it’s like steady flow. If they suddenly change pace, that’s unsteady flow. Similarly, a narrow stream of water flowing at the same speed is uniform, while a river that speeds up when going downhill illustrates non-uniform flow due to changes in elevation and area.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Pressure: The force exerted per unit area within a fluid.
-
Velocity: The speed of fluid flow at a specific point.
-
Potential Energy: Energy due to position, typically represented in terms of height in fluid equations.
-
Kinetic Energy: Energy of motion associated with the mass and velocity of the fluid.
-
Conservation of Mass: Principle of mass continuity in fluid systems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of calculating pressure difference using Bernoulli’s equation in a cyclonic wind scenario.
-
Example of how mass inflow and outflow are computed in a control volume for fluid through a pipe.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To keep that flow steady, let pressure be right; Just think of Bernoulli, and feel the might.
📖 Fascinating Stories
-
Imagine a calm river where water flows smoothly, never changing. At no moment does the river surge or fall; that’s the story of steady flow.
🧠 Other Memory Gems
-
BEP = Bernoulli’s Equation Parts: Pressure + Kinetic Energy + Potential Energy.
🎯 Super Acronyms
MEF - Mass In
- Equal Mass Out
- as in finding equilibrium in fluid flow.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Steady Flow
Definition:
A flow condition where fluid parameters, such as velocity and pressure at any given point, remain constant over time.
-
Term: Bernoulli's Equation
Definition:
An equation that describes the relationship between pressure, velocity, and elevation in an incompressible, non-viscous fluid flowing along a streamline.
-
Term: Control Volume
Definition:
A designated volume through which fluid flows, used for analyzing mass and energy equations.
-
Term: Conservation of Mass
Definition:
A principle stating that the mass inflow into a control volume equals the mass outflow, assuming steady-state conditions.
-
Term: Momentum Equation
Definition:
An equation that relates the forces acting on a fluid to the rate of change of momentum within a control volume.