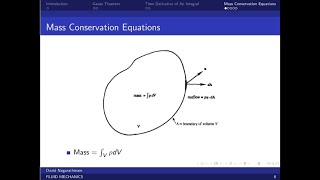
Derivation of Mass Conservation Equations
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Conservation of Mass
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Good morning everyone! Today, we’re diving into the derivation of the conservation of mass equations. Can anyone tell me what the conservation of mass means?

It means that mass cannot be created or destroyed in a closed system.

Exactly! And in fluid mechanics, this principle leads us to describe how fluid properties behave in a given control volume. Now, what do we mean by control volume?

It's a designated volume in space where we analyze mass and energy flows.

Right! When we apply the conservation of mass, we often use an integral approach to assess inflows and outflows. Does anyone remember the term used to denote our analysis method?

Is it the control volume approach?

Yes, we use control volume analysis! Remember that, as a handy acronym to recall—CVA. It’s vital in assessing the mass flow rates at the boundaries.
Integral vs. Differential Approaches
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s discuss the difference between the integral and differential approaches. Who can explain the integral approach?

The integral approach examines a larger control volume without considering the details of fluid behavior inside it.

Perfect! And what about the differential approach?

It breaks down the fluid domain into infinitely small control volumes, analyzing each point's properties like pressure and velocity.

Exactly! The differential method allows us to derive partial differential equations. What's paramount to remember here?

That the shorter dimensions converge toward a point, aiding in creating precise equations!
Reynolds Transport Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next up is the Reynolds transport theorem. Can anyone shed light on its significance in mass conservation?

It allows us to relate changes in a quantity within a control volume to net inflows and outflows across the boundaries.

Exactly! It’s foundational for deriving our equations. If we let extensive property B equal mass, how does that relate?

It helps us relate the density and velocity fields when integrating over the control volume.

Yes! When we utilize this theorem, we derive the mass conservation equation. What does it simplify to?

The rate of change of mass inside the control volume equals the net mass flux across its boundaries.
Gauss’s Divergence Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s talk about Gauss’s Divergence Theorem. Who can explain what it does?

It transforms volume integrals of divergence into surface integrals!

Exactly! By using this theorem, we can describe mass conservation more compactly. How do we express it mathematically?

Through the equation involving density and velocity components integrated over the volume.

Good! And what’s the final form of the mass conservation equation derived from this?

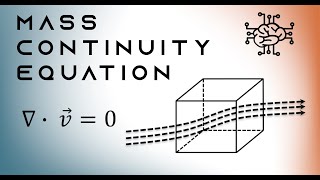
It’s expressed as the divergence of velocity equaling zero!

Perfect! Remember this equation is applicable in various fluid flow scenarios, both compressible and incompressible.
Applications in Fluid Mechanics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Lastly, how do our conservation equations apply to real-world scenarios in fluid mechanics?

They help in predicting the flow patterns in devices like pumps or turbines!

Exactly! They form the basis for computational fluid dynamics. What role do these equations play in simulation?

They allow us to model complex fluid behaviors accurately based on mass flow and velocity fields.

Great! Does anyone have a relevant example of where these equations play a crucial role?

In aerodynamics, they help in simulating airflow over aircraft wings!

Absolutely! These equations are fundamental to many engineering applications.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section explains how mass conservation equations are derived using both integral and differential approaches in fluid mechanics. It emphasizes the significance of Reynolds transport theorem and Gauss’s divergence theorem, ultimately leading to understanding the behavior of fluids in motion.
Detailed
Detailed Summary of Mass Conservation Equations Derivation
In this section, we explore the derivation of mass conservation equations applied to fluid mechanics, focusing on both integral and differential approaches. The integration approach considers a control volume as a black box, estimating mass flow through inflow and outflow. However, the differential analysis breaks down the flow domain into smaller volumes to obtain a precise representation of fluid properties such as density, velocity, and pressure.
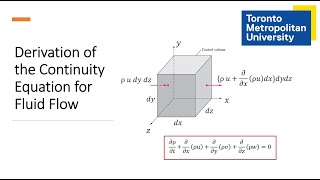
The fundamental difference between these approaches lies in handling the interior of the control volume. The section elaborates on how reducing control volume dimensions (dx, dy, dz) converges to a point, resulting in partial differential equations necessary for fluid behavior analysis.
The mass conservation equation ultimately derives from the application of the Reynolds transport theorem and Gauss's divergence theorem. The derived mass conservation equation can be compactly represented by the divergence of the velocity field equaling zero, applicable under both compressible and incompressible fluid conditions. This understanding holds immense importance for developing computational fluid dynamics algorithms.
Youtube Videos



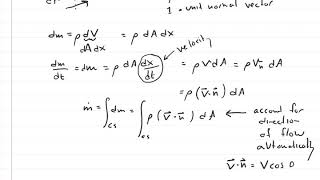
![Conservation of mass (a.k.a., continuity) [Fluid Mechanics #2]](https://img.youtube.com/vi/PFgiW7P6omE/mqdefault.jpg)


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Fluid Flow Analysis
Chapter 1 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Very good morning all of you. Today we are going to discuss on differential analysis of fluid flow which is very interesting chapters in the book of Senjal Chembala and also the F. M. White book which is the foundations of the computational fluid dynamics.
Detailed Explanation
In this chunk, the professor introduces the topic of fluid flow analysis, highlighting its significance in computational fluid dynamics (CFD). The differential analysis of fluid flow is emphasized as an exciting area of study, linking it to foundational texts in the field.
Examples & Analogies
Imagine trying to understand how water behaves when flowing through different environments, like in rivers versus pipes. This analysis helps engineers build efficient systems, very much like how fluid dynamics principles guide us in designing better transportation or plumbing systems.
Integral Approach vs. Differential Approach
Chapter 2 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Looking that let us as we discuss about integral approach in the previous classes which we generally use as a control volume. We use as a control volume considers there is a dicks is mountain over a decks and we have the control volumes to just to estimate how much of force is acting on these dicks.
Detailed Explanation
This chunk contrasts two approaches to fluid analysis: the integral approach and the differential approach. The integral approach takes a broader view, using control volumes to assess forces acting on fluids without delving into interior characteristics. In contrast, the differential approach examines each point within the flow domain to determine velocity, pressure, and density more precisely.
Examples & Analogies
Think of the integral approach like taking a large sample of soup and measuring its average saltiness without tasting every spoonful. The differential approach, however, is like meticulously tasting each spoonful to discern where the flavor changes, allowing for much more precise conclusions.
Importance of Control Volume
Chapter 3 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If you look at these problems, we consider a control volumes and we try to look at the velocity components, what could be expected inflow, outflow, also the outflow here and what could be the velocity vectors and based on that we apply the mass considerations and the momentum equations to estimate the force.
Detailed Explanation
Control volumes are central to fluid mechanics, allowing us to analyze the inflows and outflows of fluid, as well as the dynamics within that volume. By applying mass conservation and momentum equations, engineers can estimate forces acting on structures or mechanisms affected by fluid flow.
Examples & Analogies
Imagine a water tank with an inlet and outlet. By understanding how much water flows in (inflow) versus how much flows out (outflow), engineers can determine the pressure on the tank walls and ensure that it remains structurally sound.
Transition to Differential Equations
Chapter 4 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
That means instead of having so big control volumes to know the gross characteristic of the force component or the mass conservation properties we are looking it that within the flow domains if I divide into the a number of points for each point I should know what is the pressure and the velocity and what is the density variations.
Detailed Explanation
Moving from integral to differential methods requires breaking the flow domain into smaller sub-volumes, enabling the determination of specific properties like pressure, velocity, and density at each point. This transition is essential for creating differential equations that encapsulate fluid dynamics intricacies.
Examples & Analogies
Think of measuring the temperature in a room. Instead of a broad reading from one thermometer, you place many thermometers around the space to get a detailed understanding of how temperature varies, similar to how we analyze different points in fluid flow.
Setting Up Differential Equations
Chapter 5 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If my dx is tending towards 0. The dy tending towards 0 and the dz tending towards 0. That means what I am looking at the my control volume tending towards a infinitely small control volume converging towards a point value.
Detailed Explanation
The differential equations showcase fluid behavior as the control volumes approach infinitesimal sizes. As dx, dy, and dz approach zero, these equations derive governing equations for various properties, enabling analyses in terms of partial differential equations.
Examples & Analogies
Imagine gradually zooming into a picture until you see just a single pixel. At that scale, you can analyze color properties and make calculations based on specific data, much like how we analyze fluid properties at infinitesimally small control volumes.
Deriving Mass Conservation Equations
Chapter 6 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So we will get four partial differential equations which will be the one will come from mass conservation equations, three vector form equations of linear momentum okay.
Detailed Explanation
In fluid dynamics, the derivation of mass conservation equations leads to four key equations: one for mass conservation and three for linear momentum in different directions. These equations are interrelated, making them coupled equations that help in solving for fluid properties like density and velocity.
Examples & Analogies
Consider a recipe with one main ingredient (mass) and three flavors (momentum in different directions). Each component influences the others, making the overall dish (fluid behavior) dependent on how you balance these parts.
Simplifying Control Volume Analysis
Chapter 7 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Considering that if I put it for a control volumes which is a infinitely small okay which is infinitely small and for that case if I substitutes the extensive properties b is equal to m and the beta is equal to 1 ...
Detailed Explanation
When analyzing an infinitely small control volume, extensive properties such as mass can be substituted into Reynolds transport theorems. Simplified transformations allow us to establish foundational equations for mass conservation in fluid mechanics.
- Chunk Title: Using Gauss' Theorem
- Chunk Text: Let us come for deriving mass conservation equations for infinitely small control volumes ...
- Detailed Explanation: Gauss' theorem allows the transformation of volume integrals of divergence into surface integrals, providing a method to analyze mass conservation within an infinitely small control volume. It establishes a mathematical foundation for relating the behavior of fluids at all points of an analysis domain.
Examples & Analogies
Think of how a balloon breathes. Instead of only looking at the whole surface of the balloon, analyzing how many air molecules are entering or leaving through small areas helps us understand the air flow dynamics much better.
Key Concepts
-
Control Volume: A defined area for analyzing fluid mass and energy flows.
-
Integral Approach: Analysis of a whole system without focusing on its internal mechanisms.
-
Differential Approach: A method that examines every point in a flow field for detailed analysis.
-
Reynolds Transport Theorem: Links changes in control volume properties to flows across the boundaries.
-
Gauss's Divergence Theorem: Converts volume integrals to surface integrals, simplifying conservation equations.
-
Divergence: A measure of how much a vector field 'spreads out' from points.
Examples & Applications
In fluid dynamics, analyzing the flow around an airplane wing incorporates mass conservation equations to predict lift and drag forces.
A control volume analysis around a pump allows engineers to determine mass flow rates, vital for efficiency.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
To keep mass still, and flow at will, use the control volume, and study it well!
Stories
Imagine a crowded room (control volume). People (mass) can enter (inflow) and leave (outflow), but the total remains (conservation) constant unless a door is added or removed!
Memory Tools
Remember 'CVD' for Control Volume Dynamics when assessing fluid flow.
Acronyms
CVA for Control Volume Analysis—consider the flows in and out!
Flash Cards
Glossary
- Control Volume
A defined volume of space used in fluid mechanics to analyze fluid flow properties across its boundaries.
- Integral Approach
A method of analysis that treats the control volume as a whole without considering internal details.
- Differential Approach
An analytical method that examines the behavior of fluid properties at infinitesimal points in the flow field.
- Reynolds Transport Theorem
A theorem that relates changes in property within a control volume to the flux across its edges.
- Gauss Divergence Theorem
A mathematical theorem that converts volume integrals into surface integrals in fluid dynamics.
- Divergence
A measure of how much a vector field spreads out from a certain point.
Reference links
Supplementary resources to enhance your learning experience.
