Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Differential Analysis
Unlock Audio Lesson
Today, we're going to differentiate between the integral and differential approaches in fluid mechanics. Why do you think it's important to analyze fluid flow differently?
Because sometimes we need more detail than just overall effects?
Exactly! The integral approach provides a broad view, like a snapshot, while the differential approach dives into specifics at each point in the flow.
So, what does the differential approach allow us to calculate?
It helps us determine local velocity, pressure, and density variations. Think of it as viewing a movie frame by frame instead of just the highlights!
Mass Conservation Equation Basics
Unlock Audio Lesson
Now, let's talk about mass conservation. What fundamental principle do we remember regarding mass?
Mass can't be created or destroyed, right?
Correct! This leads us to the mass conservation equations. They stem from analyzing control volumes, particularly infinitesimally small volumes.
How does that work with Reynolds transport theorem?
Good question! The theorem connects changes in mass within a volume to the mass flow across its boundaries. This relationship is essential for deriving our equations.
Divergence Theorem Application
Unlock Audio Lesson
Next, we'll explore the divergence theorem. Can someone explain its significance?
It relates volume integrals to surface integrals, right?
Exactly! When we apply it in fluid mechanics, we can evaluate mass conservation across control surfaces effectively.
How do we express that mathematically?
We express it as an integral over the control volume equating to flux through the surfaces. Remember, del operator's divergence leads us to our mass equations!
Formulation of Mass Conservation Equations
Unlock Audio Lesson
Finally, let’s put it all together to derive the mass conservation equations. What do we know so far?
We know that mass in - mass out equals change in mass, plus the diversions.
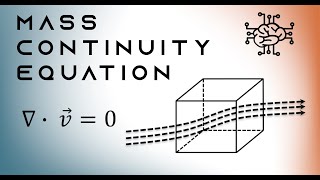
That's correct! We can derive a compact form as the divergence of velocity equals zero, applying continuity to our mass flow.
And that works for all types of flow?
Yes, whether compressible or incompressible, these conservation principles apply. Great work today!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The content discusses the differences between integral and differential approaches to fluid mechanics, focusing on mass and momentum conservation equations. It explains the significance of using infinitely small control volumes to yield partial differential equations essential in computational fluid dynamics.
Detailed
Mass Conservation Equations Derived
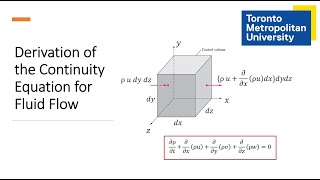
This section delves into the derivation of mass conservation equations in fluid mechanics, focusing on the transition from integral to differential analysis. The chapter begins by emphasizing the integral approach, where control volumes are utilized to assess mass and momentum within a defined space.
The teacher outlines that, while the integral approach provides insight into flow characteristics using control volumes, it does not capture the nuances of the flow field within the volume. For a more detailed analysis, the differential approach is introduced, where the flow domain is subdivided, allowing for examination of local properties such as pressure, velocity, and density.
A pivotal concept introduced is the Reynolds transport theorem, which connects the change in mass in a control volume to the mass flux across its boundaries. By considering control volumes that shrink towards an infinitely small point, one can derive partial differential equations that reflect mass conservation. The relations established are crucial for understanding the fundamental conservation laws governing fluid motion and are foundational for developing computational fluid dynamics algorithms. Ultimately, the section consolidates the mass conservation equations that stem from these principles, highlighting their applications for both compressible and incompressible flows.
Youtube Videos
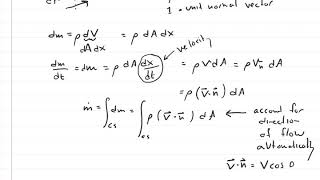
![Conservation of mass (a.k.a., continuity) [Fluid Mechanics #2]](https://img.youtube.com/vi/PFgiW7P6omE/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Control Volumes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In this case, as I again I am to repeat it to tell it, in this case we do not know the interior within this control volume, the velocity field, or the pressure field. So that is the reasons we call it the within the control volume it is just a black box.
Detailed Explanation
In fluid mechanics, a control volume is a defined region in space through which fluid may flow. When we analyze the flow using a control volume, we often treat the interior of this volume as a 'black box', meaning we do not have detailed information about the velocity or pressure of the fluid inside. This approach allows us to apply mass and momentum conservation equations to understand the forces acting on the boundaries of the control volume without needing to know the internal details.
Examples & Analogies
Imagine a sealed box filled with a mixture of gases. We cannot see inside the box and do not know the exact behavior of the gas particles. However, we can still measure how much gas is entering or leaving the box (the control volume) at its openings. This is akin to treating the inside of the box as a 'black box'.
Differential Approach of Fluid Flow Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But if you look at the same problems if I go for a next levels where each point within the flow domains... pressure and the velocity field that is the differential approach.
Detailed Explanation
The differential approach in fluid mechanics focuses on analyzing each point within a fluid flow domain. Unlike the integral approach, which looks at overall changes within a control volume, the differential approach breaks down the flow into infinitely small elements. Each point in the flow can be analyzed for pressure, velocity, and density, leading to a set of differential equations. This method gives a more detailed picture of how fluid properties vary throughout the flow.
Examples & Analogies
Consider a busy intersection with traffic lights. The integral approach might look at the total number of cars passing through the intersection, while the differential approach would analyze the speed and density of cars at every single point in the intersection to optimize traffic flow.
Reduction of Control Volumes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If my dx is tending towards 0. The dy tending towards 0 and the dz tending towards 0.
Detailed Explanation
As we reduce the dimensions of the control volume (dx, dy, dz) towards zero, we transition from a larger volume to an infinitely small point. This is essential in obtaining differential equations, as it allows us to express changes in properties like mass and momentum at each specific point in the flow. The resulting equations capture localized variations in density, velocity, and pressure, which are essential for detailed fluid dynamic analysis.
Examples & Analogies
Imagine zooming in on a large area of a river. At first, you see the river as a whole, but as you zoom in closer and closer, you begin to observe the intricate flow patterns and how they change at each small segment, eventually examining just a drop of water to see how it behaves in relation to its immediate surroundings.
Mass Conservation Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Considering that if I put it for a control volumes which is a infinitely small... control volumes of mass inflow and outflow.
Detailed Explanation
The mass conservation equation asserts that the change in mass within a control volume must equal the mass flux entering or leaving that volume. For an infinitesimally small control volume, this equation can be expressed in terms of density and volumetric flow rate, meaning the increase in mass within the volume is equal to the mass flowing in minus the mass flowing out. This fundamental principle underpins the analysis of fluid systems.
Examples & Analogies
Think of a sponge soaking up water. The mass of water inside the sponge will increase as it absorbs water (mass inflow). If you then squeeze the sponge, the amount of water that flows out equals the change in the water mass inside the sponge. This reflects the principle of mass conservation at play.
Deriving Mass Conservation Using Gauss's Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us come for the mass conservation equations for a control volume which is infinitely small... mass conservation equations derived by using divergence theorem.
Detailed Explanation
To derive mass conservation equations, we employ Gauss's theorem, which relates the volume integral of the divergence of a vector field to a surface integral over its boundary. By expressing the mass flux through the control surface and applying this theorem, we arrive at a mathematical representation of mass conservation, which states that the divergence of velocity multiplied by density equals zero. This equation is fundamental for analyzing both compressible and incompressible flows.
Examples & Analogies
Imagine a balloon being squeezed. The air (fluid) inside the balloon can be thought of as a certain amount of mass. As we squeeze it, the air must go somewhere—either it compresses further or exits through the opening. This scenario illustrates how mass is conserved even as we apply forces and change the shape of the system.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Integral Approach: A method that assesses fluid properties via control volumes.
-
Differential Approach: A technique providing local analyses of fluid flow by examining changes at each point in the flow.
-
Mass Conservation: The principle stating that mass cannot be created or destroyed, leading to conservation equations in fluid dynamics.
-
Divergence of Velocity: A measure indicating whether fluid is expanding or compressing at a point.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In analyzing water flow in a pipe, the integral approach would measure the total flow rate, while the differential approach could measure pressure at specific points along the pipe.
-
When calculating air flow across an airfoil, the mass conservation equations allow engineers to determine lift and drag at various points on the airfoil.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluid flows, where streams do turn, Conservation of mass is what we learn. Through every volume, flow must stay, What goes in must flow away.
📖 Fascinating Stories
-
Imagine a balloon filled with air. If the air escapes at the top, it must be replaced by more air coming in from the bottom. This signifies mass conservation where the total amount of air remains unchanged.
🧠 Other Memory Gems
-
To remember Reynolds Transport Theorem, think 'Changes in control lead to flows that patrol.'
🎯 Super Acronyms
Remember 'M-C-V-Flow' for Mass Conservation in Velocity Field!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Control Volume
Definition:
A defined space in fluid mechanics used to analyze the mass and momentum transfer.
-
Term: Reynolds Transport Theorem
Definition:
A fundamental theorem that relates the change in a quantity within a control volume to the flux across its boundaries.
-
Term: Divergence Theorem
Definition:
A theorem that connects volume integrals of vector fields to surface integrals, often used in the context of mass conservation.
-
Term: Mass Flux
Definition:
The mass flow per unit area, typically measured in kg/s per square meter.
-
Term: Partial Differential Equation
Definition:
An equation involving partial derivatives of a function with respect to multiple variables; essential in fluid dynamic calculations.
-
Term: Infinitely Small Control Volume
Definition:
A theoretical control volume that approaches zero dimensions, allowing local analysis of fluid parameters.
-
Term: Vector Fields
Definition:
Functions that associate a vector with every point in a certain space, used to describe fluid flow.
-
Term: Continuity Equation
Definition:
An expression based on mass conservation that indicates that mass flow is conserved in fluid flow.