Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mass Conservation
Unlock Audio Lesson
Good morning, class! Today we dive into the Mass Conservation Equation. Can anyone tell me why mass conservation is so vital in fluid mechanics?
Isn't it about ensuring that mass is neither created nor destroyed in fluid flows?
Exactly! This principle leads us to the conservation equations. We can approach this with an integral approach using control volumes or a more detailed differential approach. Would anyone like to explain what a control volume is?
It's a defined volume through which we analyze the flow of mass and momentum.
Right! We treat the control volume as a black box. Can anyone remember what we analyze through this volume?
We look at inflow and outflow velocities to determine mass balance.
Correct! In analyzing mass conservation, we particularly relate inflow and outflow to changes in mass storage within our control volume. Let's move to the differential approach.
Remember, when using control volumes, think of it as a miniature system – understanding how each part contributes to overall fluid dynamics!
Differential vs. Integral Analysis
Unlock Audio Lesson
Now, how does the differential approach differ from the integral approach?
The differential approach examines fluid properties at individual points rather than overall characteristics of a control volume.
Yes! When we consider a flow field, we need to know pressures and velocity at each point, which becomes critical in high-resolution simulations. What happens to the dimensions of your control volume in this case?
They become infinitesimally small as they tend towards a point.
Exactly! As volumes shrink to point dimensions, we derive partial differential equations that express fluid behavior. Can anyone recall how we derive the mass conservation equation through these principles?
With Reynolds transport theorem?
Spot on! That theorem provides the foundation for transforming the mass conservation law. Always remember, all equations we manipulate stem from these foundational principles of mass conservation.
Let's keep this flow in mind as we move towards understanding divergence theorem next.
Divergence Theorem Application
Unlock Audio Lesson
Next, we need to discuss how the divergence theorem applies here. What do you think the divergence of a vector generally represents in flow dynamics?
It indicates how much a fluid is expanding or compressing in space. Positive divergence means outflow, while negative means inflow.
Correct! The divergence of the velocity field is crucial in mass flow scenarios. By using the divergence theorem, we can transform the volume integral of divergence into surface integrals. How can this help us?
It relates mass flux across the control surface to changes in the mass within.
Precisely! That’s how we derive our mass conservation equations in fluid dynamics. Who can give me the general form of the mass conservation equation obtained from divergence?
It’s the divergence of the density and velocity, which is equal to zero.
Exactly! With this, we can analyze various flows in fluid mechanics, whether compressible or incompressible. Keep practicing these concepts as they build the groundwork for advanced fluid dynamics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explores the mass conservation equation as part of differential fluid flow analysis, highlighting the transition from integrative approaches using control volumes to differential equations that consider pointwise properties of fluid phenomena.
Detailed
Mass Conservation Equation- I
Overview
This section delves into the concept of mass conservation in fluid mechanics, a foundational principle used in both theoretical and computational fluid dynamics. It examines the transition from an integral approach, which considers control volumes to assess gross characteristics of fluid flow, to a differential approach that evaluates local properties within flow domains. The mass conservation equation is crucial for deriving subsequent equations related to momentum and energy in fluids, often resulting in coupled systems of partial differential equations.
Key Concepts
- Integral vs. Differential Analysis: The integral approach considers gross characteristics of a control volume, while the differential approach examines the flow characteristics at an infinitesimally small point.
- Control Volumes and Black Box Analogy: Control volumes are where mass and momentum equations apply to analyze external forces without needing internal fluid characteristics, treated as a black box.
- Mass Conservation Derivation: Utilizing Reynolds transport theorem provides insights into how mass flux inflow and outflow relate to the change in mass storage within a control volume.
- Divergence Theorem: This theorem connects volume integrals of divergence to surface integrals, critical for establishing mass conservation equations in a three-dimensional context.
- Application of Conservation Equations: The mass conservation equation holds true for both compressible and incompressible flows, reflecting on variations in density and velocity.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Differential Analysis of Fluid Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Today we are going to discuss on differential analysis of fluid flow which is very interesting chapters in the book of Senjal Chembala and also the F. M. White book which is the foundations of the computational fluid dynamics.
Detailed Explanation
In this section, we begin with the overall goal of studying fluid flow using differential analysis. This method is essential for developing computational fluid dynamics algorithms, which are used to simulate fluid flow in various engineering applications. The lecture emphasizes the importance of understanding how fluids behave under different conditions and how this knowledge is foundational for advanced study.
Examples & Analogies
Think of this as learning the weather patterns. Just like meteorologists analyze air currents to predict changes in weather, engineers use differential analysis to predict how fluids will flow under different conditions.
Control Volume Concept
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at these problems, we consider a control volume ... we apply the mass considerations and the momentum equations to estimate the force.
Detailed Explanation
The concept of a control volume is crucial in fluid mechanics. A control volume is a designated space in which fluid flow is analyzed. The analysis focuses on how fluid enters (inflows) and exits (outflows) this specified volume. By applying mass and momentum equations, we can estimate the forces acting within this volume, even though we may have limited knowledge about what is happening inside.
Examples & Analogies
Imagine a car wash. The entire car wash structure is like a control volume where cars enter, get cleaned (inflow), and exit once clean (outflow). We can analyze the water pressure and force used for cleaning, even if we don’t directly see every part of the car inside the wash.
Black Box Analogy
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The interior part of this control volume we consider as a black box ... we do not have any knowledge on the velocity and the pressure field.
Detailed Explanation
In fluid dynamics, we often treat the interior of the control volume as a 'black box'—meaning we do not need to know every detail of the fluid's behavior within it. Instead, we focus on the incoming and outgoing flows to derive important properties like pressure and velocity at the boundaries of the control volume.
Examples & Analogies
This is reminiscent of a vending machine. You put in your money (inflow) and select a drink (the machine's output). Even though you cannot see how the drink is chosen or processed inside the machine (the 'black box'), you understand the general system of inputs (money) and outputs (drinks).
Differential Approach Introduction
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I want to know what will be the pressures and what will be the velocity field ... that is what is the differential approach.
Detailed Explanation
The differential approach, in contrast to the integral approach, focuses on analyzing fluid properties at individual points within the flow field. By breaking down the control volume into infinitely small segments, we can derive equations that describe velocity, pressure, and density variations more accurately, which are necessary for detailed fluid dynamics analysis.
Examples & Analogies
Imagine using a microscope to look at a leaf. While from afar you see just a green surface, using a microscope lets you see the veins and structure of the leaf closely. Similarly, the differential approach allows engineers to analyze the intricate details of fluid behavior.
Moving Toward Partial Differential Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If my dx is tending towards 0 ... we get a set of a partial differential equations.
Detailed Explanation
As the dimensions of our control volume shrink toward zero, we can express the mass conservation and momentum equations in the form of partial differential equations. This transition is critical for formulating the mathematical models needed for fluid dynamics, allowing us to analyze the system as a series of interconnected equations.
Examples & Analogies
This is akin to zooming in on a map. When you start with a wide overview of an area but zoom in and notice street layouts and building details, you obtain a clearer understanding of your surroundings, just as detailed equations give a clearer view of fluid behaviors.
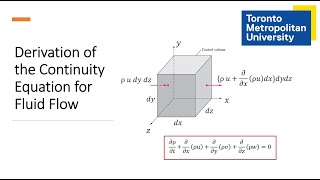
Deriving Mass Conservation Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us as we discuss about the Reynolds transport theorems ... the mass conservation equations.
Detailed Explanation
We can derive the mass conservation equations using Reynolds transport theorem and linking it to the concept of control volumes. This theorem allows us to equate changes in mass within a control volume to the net mass flows across its boundary. When we apply this theorem to a control volume, it leads us to express the mass conservation equations succinctly.
Examples & Analogies
Picture a savings account. The deposits (mass inflows) and withdrawals (mass outflows) over time change the account balance (mass within the volume). The balance reflects the conservation principle, where what's added and taken away defines the total amount.
Understanding Mass Flux
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at this part which is very simplifications part for a control volumes that rate of change of the mass within the control volume ... how much of mass flux is changing within the control volume.
Detailed Explanation
Mass flux refers to the rate of mass flowing through a surface per unit time and is essential for mass conservation. In calculations, we express mass flux as the density multiplied by the velocity. Understanding how to calculate mass flux allows us to quantify the inflow and outflow while studying a control volume.
Examples & Analogies
Think of a water hose. The amount of water flowing out of the hose in a second (mass flux) can be calculated by knowing how fast the water flows (velocity) and the water's density. This is similar to how we calculate mass flow in fluid mechanics.
Using Gauss’s Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us come for deriving mass conservation equations for infinitely small control volumes ... it helps us to transform a volume integral of a divergence of a vector.
Detailed Explanation
Gauss's Theorem allows us to relate the divergence of a vector field within a volume to the flow across the boundary of that volume. By applying Gauss's theorem, we can derive the mass conservation equations, making it easier to handle complex fluid systems by only needing to consider the boundary interactions.
Examples & Analogies
Consider a balloon filled with air. The air inside (volume) has molecules moving around (divergence). If you let some air out (surface integral), the change inside the balloon can be calculated easily by counting the amount that leaves, simplifying the complex interactions of air molecules.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Integral vs. Differential Analysis: The integral approach considers gross characteristics of a control volume, while the differential approach examines the flow characteristics at an infinitesimally small point.
-
Control Volumes and Black Box Analogy: Control volumes are where mass and momentum equations apply to analyze external forces without needing internal fluid characteristics, treated as a black box.
-
Mass Conservation Derivation: Utilizing Reynolds transport theorem provides insights into how mass flux inflow and outflow relate to the change in mass storage within a control volume.
-
Divergence Theorem: This theorem connects volume integrals of divergence to surface integrals, critical for establishing mass conservation equations in a three-dimensional context.
-
Application of Conservation Equations: The mass conservation equation holds true for both compressible and incompressible flows, reflecting on variations in density and velocity.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In fluid dynamics, an example of mass conservation is when water flows into a tank through an inlet; the mass flow rate at the inlet must equal the flow rate out to ensure mass balance.
-
When analyzing air flowing through a pipe, the mass conservation principle can show that changes in pipe diameter result in varying velocities to maintain constant mass flow.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Flow with ease, mass must stay, in and out, but not away.
📖 Fascinating Stories
-
Imagine a magician who can only transport objects without creating new items or destroying them, representing mass conservation.
🧠 Other Memory Gems
-
CVD = Control Volume Dynamics - remembering relationships between flow properties at a control volume.
🎯 Super Acronyms
FLOWS stands for
- Flow
- Inflow
- Outflow
- With Storage - remembering how mass moves in a system.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Control Volume
Definition:
A defined region in space through which fluid flows, used for analyzing changes in mass, momentum, and energy.
-
Term: Divergence Theorem
Definition:
A theorem that relates the volume integral of the divergence of a vector field to the surface integral of the vector field over the boundary surface.
-
Term: Reynolds Transport Theorem
Definition:
A theorem that provides a relationship between the rate of change of extensive properties within a control volume and the flux of the properties across its boundary.
-
Term: Mass Flux
Definition:
The mass flow rate per unit area, expressed as kilograms per second per unit area.
-
Term: Differential Equation
Definition:
An equation that relates a function with its derivatives, used for analyzing continuous systems and fluxes.