Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Divergence Theorem
Unlock Audio Lesson
Good morning, class! Today we delve into the Divergence Theorem. Can anyone tell me what they think a divergence means in fluid mechanics?
Is it related to how fluid expands or contracts within a volume?
Exactly! The divergence measures the rate at which 'stuff' is expanding or compressing at a point. We can use it in safety and environmental assessments. Let's remember: Divergence acts like a 'source' or 'sink' of fluid. If we denote it by 'D', we can think of it as 'D = Source'.
So, more divergence implies more fluid is flowing out from a point?
Correct! And vice versa. Now, when we apply the Divergence Theorem, we connect these concepts of divergence to volumes and surfaces. Can anyone summarize the mathematical relationship?
Is it the integral of divergence over a volume equals the surface integral over its boundary?
Precisely! The formula captures that beautifully. In fluid mechanics, we often need this relationship for mass conservation. We'll go into details about deriving mass conservation equations in our next session.
Deriving Mass Conservation Equations
Unlock Audio Lesson
Let's build upon our previous discussion. Who remembers how we can derive mass conservation equations using the Divergence Theorem?
We can express the mass flowing into the control volume and out of it using integrals?
Yes! In order to derive the equation, we start by considering a control volume and applying the Divergence Theorem to the mass flux. Can someone explain what mass flux is?
It’s the mass per unit time flowing through a unit area!
Great! Remember: mass flux \( = \rho v \), where \( \rho \) is density and \( v \) is velocity. Now, if we set up our equations based on the inflow and outflow, how do we express that mathematically?
We could set up an equation that states the change in mass within our volume equals the mass inflow minus the mass outflow.
"Absolutely! That's the essence of the mass conservation principle. Recapping, we derived \( \nabla \cdot (
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The Divergence Theorem allows us to connect volume integrals of the divergence of a vector field to surface integrals across its boundary. This theorem is foundational in fluid mechanics for deriving equations related to mass conservation and understanding fluid flow behavior in different conditions.
Detailed
Detailed Summary of the Divergence Theorem
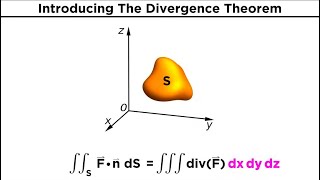
The Divergence Theorem, also known as Gauss's Theorem, establishes a crucial link between the volume integrals of the divergence of a vector field and the surface integrals over the surface that bounds the volume. In fluid mechanics, this theorem is instrumental in the analysis of fluid flow, especially regarding mass conservation.
The principle states that the integral of the divergence of a vector field over a volume can be transformed into a surface integral over the boundary of that volume. Mathematically, this relationship is expressed as:
\[ \int_V (\nabla \cdot \mathbf{F}) \, dV = \int_S \mathbf{F} \cdot \mathbf{n} \, dA \]
where \( V \) is the volume, \( S \) is the boundary surface, and \( \mathbf{n} \) is the outward unit normal to the surface. This theorem has wide applications, including the simplification of complex flow problems where it helps derive mass conservation equations effectively. The resultant equations are fundamental for analyzing both incompressible and compressible flows, leading to a deeper understanding of momentum and energy distribution within fluids.
Through the differential analysis approach, the understanding of variations in density, pressure, and velocity is achieved, which is crucial for solving fluid dynamics problems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to the Differential Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Fluid Mechanics
Prof. Subashisa Dutta
Department of Civil Engineering
Indian Institute of Technology-Guwahati
Lec 24: Mass Conservation Equation- I
Very good morning all of you. Today we are going to discuss on differential analysis of fluid flow...
Detailed Explanation
In this introductory segment, the speaker emphasizes the importance of differential analysis in fluid dynamics and contrasts it with previously discussed integral approaches. The objective of differential analysis is to derive specific characteristics of fluid motion at each point in the flow domain. This approach is crucial for developing computational fluid dynamics algorithms, providing detailed insights into pressure, velocity, and density variations within a flow.
Examples & Analogies
Think of trying to understand a river's flow not just by measuring the overall speed at one point (integral approach) but by examining the speed of the water at many tiny locations throughout the river (differential approach). This detailed examination reveals how different factors like rocks or bends in the river affect the flow locally.
Understanding Control Volumes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
...if you look at these problems, we consider a control volumes and we try to look at the velocity components...
Detailed Explanation
The concept of control volumes is introduced, where a specific volume of fluid flow is analyzed. The control volume can be thought of as a 'box' in which fluid properties (like velocity and pressure) are evaluated at inlet and outlet points. This method allows for assessing forces and mass conservation without knowing the internal flow details, hence the term 'black box' approach.
Examples & Analogies
Imagine you have a water tank with pipes on the top and bottom. You want to find out how much water is flowing in and out without looking inside the tank. By measuring how fast water is coming in and going out, you can determine changes in the water level using the control volume approach.
Differential Approach vs Integral Approach
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
...if I want to know what will be the pressures and what will be the velocity field that is the differential approach...
Detailed Explanation
The speaker discusses the difference between differential and integral approaches to fluid analysis. The differential approach focuses on examining each point within the flow domain, allowing for precise calculations of pressure, velocity, and density at every point. This contrasts with the integral method, which looks at larger volumes and averages properties throughout those volumes.
Examples & Analogies
Consider a team of doctors monitoring patients in a hospital. The integral approach is like checking the overall health of a ward (how many patients are stable versus unstable), while the differential approach is akin to closely monitoring each patient's individual vital signs.
Concept of Mass Conservation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
...if I substitute on these Reynolds transport theorems, anyway you know it, this part, the system part will be the zero...
Detailed Explanation
Mass conservation in fluid mechanics asserts that mass cannot be created or destroyed within a closed system. The speaker describes how this principle is formulated using Reynolds transport theorem, which relates the rate of change of mass within a control volume to the mass that flows in and out through its surface. This principle is foundational in deriving the equations governing fluid motion.
Examples & Analogies
Think of a balloon filled with air. If no air is added or released, the mass of air inside remains constant. If you slowly release air, the mass decreases, demonstrating the mass conservation principle as the total amount of air inside the balloon changes only with inflow or outflow.
Gauss Theorem and Divergence Concept
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
...let us come for deriving mass conservation equations for infinitely small control volumes...
Detailed Explanation
The discussion shifts to Gauss's theorem, which relates the divergence of a vector field (like velocity) over a volume to the flow across its boundary. This theorem is applied to express mass conservation equations in fluid mechanics. By transforming a volume integral of divergence into a surface integral, it helps quantify how mass flows in and out of a control volume, enabling the derivation of mass conservation equations.
Examples & Analogies
Imagine a water fountain where water flows out. The Gauss theorem helps you understand that the amount of water spraying out (surface integral) is directly related to the total water content inside the fountain (volume integral), helping ensure the fountain can keep flowing continuously.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Divergence: Measures the rate of change of density in a fluid.
-
Control Volume: A region through which fluid flows, used to apply the Divergence Theorem.
-
Mass Conservation: The principle that mass cannot be created or destroyed, only transformed.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a pipe with varying diameter, the flow rate is constant, but the velocity changes due to the area variation, demonstrating mass conservation principles.
-
In atmospheric studies, the Divergence Theorem helps in analyzing wind patterns over large geographical areas.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Divergence is the spread, in a fluid, it is said; more outflow means a source, less means a sink with force.
📖 Fascinating Stories
-
Imagine a water balloon. When you squeeze, water flows out — that’s a source! When it’s still, there’s no flow, like a sink. The Divergence Theorem is the bridge that connects these observations.
🧠 Other Memory Gems
-
To remember Divergence, think of 'D' for 'Diverging' fluid; D = Source or Sink. It's all about direction!
🎯 Super Acronyms
D for Divergence, I for Inflow, O for Outflow, N for Net Change (D = I - O).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Divergence Theorem
Definition:
A fundamental theorem in vector calculus that relates the surface integral of a vector field over a closed surface to the volume integral of its divergence in the region bounded by the surface.
-
Term: Mass Flux
Definition:
The mass flow rate per unit area, often expressed as the product of density and velocity.
-
Term: Control Volume
Definition:
A defined volume in fluid mechanics through which fluid flow is analyzed.