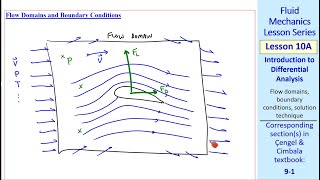
Differential Approach
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Differential Approach
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Good morning, everyone! Today, we'll explore the differential approach in fluid mechanics. Can anyone tell me how this approach differs from the integral approach?

I think the integral approach looks at control volumes, while the differential approach focuses on individual points, right?

Exactly! The integral approach treats the control volume like a black box. The differential approach, however, allows us to analyze the pressure and velocity at every point in the fluid. This precision is essential for computational fluid dynamics. Let’s remember this as the ‘black box vs. detailed point view’ difference.

So, what equations do we derive using the differential approach?

Good question! We derive the mass conservation and momentum equations, which are based on partial differential equations.
Mass Conservation in Differential Approach
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's dive into mass conservation today. Who can explain what this means in terms of fluid flow?

I think it relates to the flow of mass in and out of a control volume.

Absolutely! In the differential approach, we can analyze how mass changes over the control volume using partial derivatives. This lends itself to creating specific equations that discuss mass inflow and outflow. Can anyone repeat a key concept here?

The rate of change in mass is equal to the inflow minus the outflow?

Exactly! This leads us to our foundational equations in fluid mechanics.
Momentum Equations in the Differential Approach
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let’s connect mass conservation to momentum. How do we relate these two?

I believe momentum is affected by mass and velocity, right?

That's correct! The momentum equations account for how velocity changes, incorporating the fluid's density as well. This allows for a fully coupled understanding in fluid dynamics.

Are these derived using similar techniques as mass conservation?

Yes! We derive them using the same principles of differential equations, but we need to ensure all variables are coupled correctly.
Application of the Differential Approach
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Why do you think understanding the differential approach is crucial for engineering fields, particularly in civil engineering?

It’s probably because it helps in predicting fluid behavior in structures and systems.

Exactly! Applying these principles allows engineers to design better systems. Remember to think of the differential approach as a detailed roadmap for fluid analysis.

Can we use simulation software with these equations?

Definitely! Computational fluid dynamics relies on these differential equations to simulate fluid flows accurately.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
This section discusses the differential approach in fluid mechanics, emphasizing the shift from a broader control volume analysis to focusing on individual points within a fluid flow. Key concepts such as the mass conservation and momentum equations are introduced, highlighting how differential equations enable the determination of pressure and velocity fields, which are essential for computational fluid dynamics.
Detailed
Differential Approach
This section explores the differential approach in fluid mechanics, which provides a more precise understanding of fluid flow compared to the integral approach. The integral approach considers a control volume and does not provide information about the interior conditions (pressure and velocity fields), treating this area as a 'black box'. In contrast, the differential approach analyzes fluid characteristics at infinitely small control volumes or points within the fluid domain. This method allows for the derivation of partial differential equations that describe mass conservation and momentum, crucial for computational fluid dynamics. By reducing the dimensions of the control volume (dx, dy, dz) to zero, we derive equations that link the velocity, pressure, and density fields throughout the flow. Ultimately, this section establishes foundational concepts necessary for understanding fluid dynamics and computational methodologies.
Youtube Videos







Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Differential Approach
Chapter 1 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Differential analysis of fluid flow is projected as a more detailed approach than the integral method. In the integral approach, we look at large control volumes without knowing the interior details, whereas the differential approach focuses on smaller elements within the flow.
Detailed Explanation
The differential approach to fluid dynamics allows for the examination of every minute point in the flow rather than only considering larger volumes. By breaking down the flow domain into smaller intervals, we can analyze pressures, velocities, and density variations at every point, offering a more precise understanding of the flow behavior.
Examples & Analogies
Think of the differential approach like using a microscope to examine a small section of fabric. Instead of just viewing the whole cloth (integral approach), you look closely at the individual threads (differential approach) to understand how they intertwine and contribute to the overall pattern.
Concept of Control Volumes
Chapter 2 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In the integral approach, we consider the control volume as a 'black box'. We determine forces acting on this box without knowledge of the velocity or pressure within. The differential approach, however, requires us to analyze infinitesimally small control volumes within the flow.
Detailed Explanation
Understanding the control volume is critical in fluid dynamics. In an integral analysis, we see only the net forces acting on the control volume without insight into internal flows. In contrast, the differential approach corresponds to analyzing smaller volumes where each small division can reveal internal velocities, pressures, and density variations.
Examples & Analogies
Imagine a locked box where you can't see what's inside (integral). You can only weigh it to know its effects. Now, if you had the chance to open the box and observe each individual item inside (differential), you'd understand how each one contributes to the overall weight.
Reduction of Control Volume Size
Chapter 3 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The dimensions of the control volume can be reduced to an infinitely small value (dx, dy, dz → 0). This allows us to derive differential equations suitable for analyzing mass conservation and momentum.
Detailed Explanation
By considering the dimensions of our control volume as infinitesimally small, we can transition from discrete observations to differential equations. This transition establishes relationships between various properties (like velocity and pressure) at a specific point, enabling us to analyze fluid flow with great precision.
Examples & Analogies
Think of how scientists study tiny particles using particle accelerators, breaking them down to their smallest components. Just as those tiny elements help understand the physics behind larger constructs, reducing control volumes helps derive fundamental equations of fluid motion.
Differential Equations for Fluid Dynamics
Chapter 4 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The resulting differential equations from this approach are primarily four: one for mass conservation and three corresponding to linear momentum in three dimensions.
Detailed Explanation
These four equations emerge as key elements for modeling fluid behavior. The mass conservation equation ensures that mass is neither created nor destroyed in the flow, while the momentum equations account for the forces acting in all three spatial dimensions. Together, they form the backbone of fluid dynamics analysis.
Examples & Analogies
Just like a recipe needs the right balance of ingredients (measurement of flour, sugar, etc.) to come out perfect, these four equations ensure that the physical laws governing fluids are balanced and accurately represent real-world phenomena.
Understanding the Divergence Concept
Chapter 5 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The concept of divergence will play a critical role in visualizing fluid flow. Positive divergence indicates an outward flow (source), whereas negative divergence indicates inward flow (sink).
Detailed Explanation
Divergence quantifies the change in flow velocity at a point, providing essential insights into sources and sinks within the fluid. A positive divergence suggests that fluid is being created or moving outward at that point, while a negative divergence indicates that fluid is being absorbed or drawn inward.
Examples & Analogies
Consider a balloon being blown up (positive divergence) versus water being sucked out of a sponge (negative divergence). In both scenarios, you see how materials flow in or out, which can be analyzed using the concept of divergence.
Application of Gauss's Theorem
Chapter 6 of 6
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Gauss's Theorem relates the volume integral of the divergence of a vector to the surface integral over the boundary of the volume. This theorem is pivotal in deriving the mass conservation equations.
Detailed Explanation
Gauss's Theorem allows us to convert complex integrals over volumes into simpler surface integrals. This simplification is crucial for solving fluid mechanics problems, especially in systems where the flow is complex. By defining a control surface, we can analyze fluid behavior more efficiently.
Examples & Analogies
Imagine trying to count the number of raindrops falling into a pond (volume). Instead of counting each drop directly, you might count how many drops are hitting the pond's perimeter (surface) over a certain time, then extrapolate to estimate how many are falling in total. Gauss's theorem essentially enables this clever calculation.
Key Concepts
-
Differential Approach: A method analyzing fluid dynamics at individual points rather than over control volumes.
-
Mass Conservation: Principle stating that the mass within a control volume remains constant unless there is an inflow or outflow.
-
Momentum Equations: Relationships used to describe the conservation of momentum within fluid dynamics.
Examples & Applications
Analyzing a small cube of fluid to derive velocity and pressure conditions at each point leads to the formulation of the mass and momentum equations.
Using the divergence theorem to transform the volume integral of divergence into surface integrals allows for practical applications in fluid flow problems.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When fluid flows without a hitch, mass and momentum never switch.
Stories
Imagine a tiny water droplet moving through the air. Each point it passes shows its speed and pressure, guiding the overall flow like a GPS for fluid dynamics.
Memory Tools
D - Density, V - Velocity, M - Mass Conservation. Just DVM your way through fluid analysis!
Acronyms
DAMP - Differential Analysis in Mass and Pressure, helps keep flow in check.
Flash Cards
Glossary
- Control Volume
A defined region in space used to analyze fluid flow and properties.
- Mass Conservation
Principle stating that mass cannot be created or destroyed within a closed system.
- Momentum
The product of mass and velocity, indicating the motion of an object.
- Differential Equations
Mathematical equations that relate a function with its derivatives.
- Divergence Theorem
Mathematical statement relating the flow of a field through a surface to the behavior of the field inside the volume.
Reference links
Supplementary resources to enhance your learning experience.
