Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Integral vs Differential Approaches
Unlock Audio Lesson
Today, we will examine the integral and differential approaches to analyzing fluid flow. The integral method focuses on control volumes, while the differential approach provides insights at the individual point level. Why do you think understanding both methods is important?
I think it helps in analyzing fluid behavior on different scales.
Exactly! The integral approach gives us a broader view, helping to estimate forces across larger volumes. Can anyone explain what we mean by treating the interior of a control volume as a 'black box'?
It means we don't concern ourselves with the internal velocity or pressure fields.
Correct! By focusing on the mass and momentum equations, we can analyze the total force acting on our volume.
Differential Analysis Components
Unlock Audio Lesson
Now, let's talk about the differential approach. As we reduce our control volume size towards a point, what happens?
We can derive partial differential equations that describe mass and momentum better!
Absolutely! When we get to an infinitely small control volume, we can start composing those crucial equations. Does everyone remember the four essential partial differential equations we derive?
One for mass conservation and three for linear momentum!
Right! And those equations are interlinked, reflecting the relationships between density, velocity, and pressure fields.
Gauss Theorem and Mass Conservation
Unlock Audio Lesson
Let's focus on Gauss's Theorem and how it's linked to mass conservation. Who can summarize what Gauss’s theorem states?
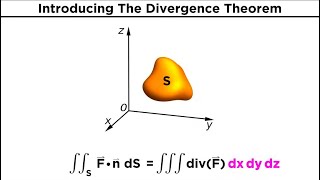
It transforms a volume integral of divergence of a vector into a surface integral over the boundary of that volume.
Precisely! We can apply that to our conservation equations. How does this relationship facilitate mass flow analysis?
It allows us to analyze mass inflow and outflow more conveniently!
Exactly! Using this method, we establish a direct connection between changes in mass and velocity across fluid flow, crucial for our derived equations.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section highlights the transition from integral to differential approaches in fluid mechanics, particularly using Gauss Theorems for mass conservation. It emphasizes how analyzing fluid dynamics at infinitesimally small control volumes leads to the derivation of key equations governing mass and momentum.
Detailed
In fluid mechanics, Gauss Theorems play a crucial role in the analysis of mass conservation. This section discusses the difference between integral and differential approaches to fluid flow. The integral approach looks at the behavior of fluid dynamics within control volumes, while the differential approach focuses on properties at an infinitesimal level, leading to the formulation of partial differential equations. By shrinking control volumes towards zero dimensions in Cartesian coordinates, four fundamental equations emerge: one for mass conservation and three for linear momentum in vector form. The section further elucidates the application of Reynolds transport theorems and concludes with a methodical derivation of mass conservation equations through Gauss’s divergence theorem, reinforcing the relationship between volume and surface integrals in fluid dynamics.
Youtube Videos
![[CFD] Gauss-Seidel Method in CFD](https://img.youtube.com/vi/ymIvps7pgRk/mqdefault.jpg)
![[CFD] Green-Gauss Cell-Based and Node-Based Gradient Schemes](https://img.youtube.com/vi/oeA1Bg9GqQQ/mqdefault.jpg)
![[CFD] Calculating the Cell Volume](https://img.youtube.com/vi/x2CsJUE8bZo/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Gauss Theorems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us come for the mass conservation equations for a control volume which is infinitely small. When you go for that let us as we discuss about the Reynolds transport theorems in previous classes we will apply this here but only our control volume is infinitely small.
Detailed Explanation
In this chunk, the instructor introduces the context in which Gauss Theorems will be applied, specifically regarding mass conservation equations. The focus is on controlling an infinitely small volume, which simplifies the analysis of mass flow in fluid dynamics.
Examples & Analogies
Think of a drop of water in a swimming pool. If we want to observe how the water is moving, we can imagine looking at an infinitely small part of that drop. Just like measuring the tiny area where the drop interacts with the surrounding water can help us understand flow patterns, analyzing an infinitely small control volume can reveal important details about mass conservation.
Reynolds Transport Theorem Application
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I consider that the basic equations what I will get it that is very simple conservation of mass for infinitely small control volume that does not matter it for us but if you look at the Reynolds transport theorems then I will get these equations...
Detailed Explanation
This chunk discusses applying Reynolds transport theorem to derive mass conservation equations for an infinitely small control volume. The theorem relates changes in a quantity within a control volume to the inflow and outflow across the volume's boundaries. Here, the focus is on linking density with volumetric flow.
Examples & Analogies
Imagine measuring how much sand is poured (inflow) into a small box compared to how much sand gets removed (outflow). The Reynolds transport theorem helps us manage these measurements to ensure that the sand doesn't suddenly disappear or accumulate. It reminds us that the total amount must be conserved.
Divergence Theorem Overview
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us look at the what is the the divergence between the two vectors. And mostly as we are using the fluid mechanics, we are looking at divergence field of velocity field...
Detailed Explanation
In this part, the idea of divergence is explained. Divergence is a measure of how much a vector field spreads out from a point. In fluid mechanics, analyzing velocity divergence helps identify sources (where fluid is flowing out) or sinks (where fluid is flowing in).
Examples & Analogies
Consider a balloon being inflated. As air rushes into the balloon, the velocity of air at the opening is high, while at the back of the balloon, it’s much lower. The difference in these velocities can be thought of as a measure of divergence, showing how quickly the balloon is expanding due to the air being pumped in.
Gauss Theorems Definition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is a conservation of mass conservation equations that it helps us transform a volume integral of a divergence of a vector...
Detailed Explanation
This section formally defines Gauss' Theorem, which states that the volume integral of the divergence of a vector field can be transformed into a surface integral over the boundary of the volume. This is central to deriving mass conservation equations as it allows for transitioning from volume to surface calculations.
Examples & Analogies
Imagine a balloon filled with water. If we want to look at how water is flowing in or out of it, instead of trying to incorporate the entire balloon's interior, we could simply measure the water entering or leaving through the balloon's surface. The Gauss Theorem helps relate these measurements effectively.
Final Formulation of Mass Conservation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I look at these equations, equations 2 and this is what the equations 1, which is from the Reynolds transport theorems...
Detailed Explanation
The final chunk consolidates the concepts discussed by arriving at the mass conservation equations derived using the divergence theorem. It leads to a significant conclusion where mass flux is characterized via differential forms, reiterating important principles in fluid mechanics.
Examples & Analogies
Think of a water tank where water is entering and leaving through pipes (the surface integrals). By applying the insights from the Gauss Theorems, we can predict how the water level changes over time and ensure that flow is balanced—akin to managing a water supply system.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Integral and Differential Analysis: Understanding two major approaches in fluid dynamics.
-
Control Volumes: The volumes are defined for analyzing mass and momentum.
-
Gauss's Theorem: The relationship between volume integrals and surface integrals.
-
Mass Conservation: The fundamental principle that mass can neither be created nor destroyed in fluid flow.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
- Analyzing a cylindrical control volume around a pipe to determine flow rates at inflow and outflow.
-
- Applying Gauss's theorem to compute the mass flow through a defined surface around a spherical control volume.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In control volumes wide, mass flows in and out with pride.
📖 Fascinating Stories
-
Imagine a balloon, filled and squeezed; the air flows in and out, while the mass stays seized.
🧠 Other Memory Gems
-
Remember Gauss - 'V for Volume, A for Area', to relate integrals of vector behavior.
🎯 Super Acronyms
D.V.M
- Differential
- Volume
- Mass - key to fluid mechanics essence.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Integral Approach
Definition:
A method in fluid mechanics that analyzes mass and momentum over large control volumes.
-
Term: Differential Approach
Definition:
An analysis method focusing on fluid properties at an individual point, leading to partial differential equations.
-
Term: Control Volume
Definition:
A specified volume in space through which fluid flows for analysis.
-
Term: Gauss's Theorem
Definition:
A mathematical theorem connecting volume integrals of divergence of a vector field to surface integrals over the boundary.
-
Term: Mass Conservation Equation
Definition:
An equation that expresses the principle of mass conservation in fluid flow.