Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Collision Theory
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Welcome everyone! Today we're diving into collision theory. Can someone remind me why collisions are important for reactions?
I think molecules need to collide in order to react, right?
Exactly! But it's not just about colliding; they must collide with enough energy and in the right orientation. This is where the idea of effective collisions comes in. Can anyone guess what it means to have an 'effective collision'?
Does that mean the molecules are hitting each other in such a way that bonds can break and new ones can form?
Spot on! Effective collisions are those that lead to products. To quantify how often these collisions occur, we use the concept of the steric factor. Does anyone know what the steric factor represents?
Is it like a measure of how well the molecules line up when they collide?
Precisely! The steric factor, or p, is crucial for understanding how different molecular shapes can affect the likelihood that a collision will be effective.
So, if p is small, does that mean fewer reactions happen?
Yes, a smaller p indicates that only a few collisions occur with the proper orientation, reducing the reaction rate.
Does this mean that all collisions don't lead to reactions?
Exactly! Not all collisions are productive. This leads us to consider how factors like temperature and concentration influence reaction rates. Let's explore that further. Great discussion, everyone!
Mathematics of Collision Frequency
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we've established the basics of effective collisions, let's talk about collision frequency. Can anyone remind us how we express the frequency of collisions in the gas phase?
I think it has something to do with the concentrations of the reactants?
Yes! The collision frequency can be formulized. When we consider two gas species, A and B, their collision frequency, Z_AB, is influenced by their concentrations and the collision cross-section. Do you remember the formula for this?
It's Z_AB = N_A * N_B * ฯ_AB, right?
Correct! Where N_A and N_B are the number densities of A and B, and ฯ_AB is the area that they present for collisions. As we increase the concentrations, what happens to the collision frequency?
It increases! So if both concentrations are doubled, does that mean the collision frequency quadruples?
Exactly! That's a key point from collision theory. And you can visualize this effect as we move forward. Improvising on these relationship helps us understand how to manipulate reaction conditions better!
So higher concentrations lead to more effective collisions?
Yes! But remember, it's not just about frequency; the energy of collisions also matters, which we will explore next.
Maxwell-Boltzmann Distribution and Energy
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's shift our focus to energy. Who can tell me how temperature impacts the energy of molecules in a gas?
I remember that higher temperatures mean faster-moving molecules, right?
That's correct! And that relates to the Maxwell-Boltzmann distribution, which shows how kinetic energies are distributed among molecules at a specific temperature. Can someone describe what happens to this distribution as temperature increases?
The distribution broadens and shifts toward higher energies, which means more molecules can exceed the activation energy?
Exactly! This is a significant concept because it illustrates why many reaction rates double with every increase of 10โ20 K in temperature. Itโs a practical application of collision theory. Can anyone summarize how this affects reaction rates?
So, as temperature increases, more effective collisions occur because more molecules can reach the required energy for a reaction?
Well said! This connection is foundational in kinetics. All right, to wrap up, can someone recap the key points we've discussed today?
We learned that effective collisions require both energy and proper orientation, that the steric factor measures orientation, and that temperature influences how many molecules have enough energy!
Great summary! Keep these concepts in mind as we continue to explore reaction rates.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
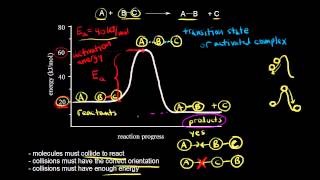
In this section, we delve into collision theory, underscoring that reactions occur only when reactants collide effectively with the necessary orientation and energy. The steric factor is introduced to quantify how molecular structure affects collision outcomes, significantly influencing reaction rates.
Detailed
Effective Collisions and Steric Factor
This section elaborates on the fundamental aspects of collision theory as it pertains to chemical reactions. According to collision theory, for any reaction to take place, the reactants must collide with sufficient energy and the correct orientation. An essential concept introduced here is the steric factor (p), which quantifies the likelihood of effective collisions based on molecular orientation.
Key Points
- Steric Factor (p): The steric factor accounts for the orientation needed during collisions. For simple atomic collisions, p is close to 1; however, larger or more complex molecules may have much smaller values, indicating fewer effective collisions.
- Collision Frequency: The frequency of collisions between reactant molecules in the gas phase can be mathematically expressed, leading to an understanding of how increased concentrations, higher temperatures, and larger collision cross-sections can impact the rate of reactions.
- MaxwellโBoltzmann Distribution: At any given temperature, the distribution of molecular energies follows the MaxwellโBoltzmann distribution, which illustrates that as temperature rises, a greater proportion of molecules have energies that exceed the activation energy required for reactions.
Understanding the interplay between collision frequency, energy distribution, and molecular orientation provides insight into how reaction rates can be manipulated and predicted, laying groundwork for advanced kinetics studies.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Steric Factor Overview
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
3.2.1 Steric Factor
The steric factor p accounts for the requirement that molecules must be oriented correctly when they collide in order for bonds to break and form. For simple atomโatom collisions, p might be close to 1. For larger or more complex moleculesโwhere only a small fraction of collisions align reactive groups properlyโp can be very small (like 10โปยณ or even 10โปโด).
Detailed Explanation
The steric factor (p) is a key concept in collision theory that describes how the orientation of molecules during collisions affects the likelihood of a reaction occurring. When two molecules collide, it's not enough for them to just hit each other; they must also align in a specific way for bonds to break and form new ones. For small, simple molecules, this means that almost every collision could lead to a reaction, which gives a steric factor close to 1. However, for larger and more complex molecules, the correct orientation during a collision is less likely, resulting in a much smaller steric factor, sometimes as low as 0.001 to 0.0001. This stark difference highlights how molecular size and complexity can significantly affect reaction rates.
Examples & Analogies
Imagine trying to fit two blocks together in a specific shape; if you just throw the blocks together without considering how they align, they won't connect properly. However, if the blocks are small and simple, you might be able to connect them easily from almost any angle. With larger, more complicated shapes, you need to ensure they face the right direction to fit together at all.
Collision Frequency in the Gas Phase
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
3.2.2 Collision Frequency in the Gas Phase
In the ideal-gas approximation, the total collision frequency Z_AB (number of collisions per unit time per unit volume) between species A and B can be expressed as:
Z_AB = N_A ร N_B ร ฯ_AB ร โ(8ยทkยทT / (ฯยทฮผ_AB)),
where
- N_A and N_B are the number densities (number of molecules per unit volume) of A and B.
- ฯ_AB is the collision cross-section of A and Bโthat is, the effective โtarget areaโ for collision.
- k is Boltzmannโs constant (1.381ร10โปยฒยณ JยทKโปยน).
- ฮผ_AB is the reduced mass of A and B, defined by ฮผ_AB = (m_Aยทm_B)/(m_A + m_B), where m_A and m_B are the masses of one molecule of A and B (in kilograms).
- The square root term, โ(8ยทkยทT / (ฯยทฮผ_AB)), arises from the average relative speed of A and B as given by the MaxwellโBoltzmann distribution.
Thus, collision frequency increases with increasing number densities, larger collision cross-sections, and higher temperature.
Detailed Explanation
The total collision frequency (Z_AB) between two types of gas molecules (A and B) tells us how often they collide with each other in a given space over a certain time. This calculation involves several factors: the concentrations of the gases (N_A and N_B), the effective target area for collisions (ฯ_AB), and a mathematical representation of their average speed at a particular temperature. As you can see from the equation, increasing the number of molecules (higher N_A and N_B), making the molecules larger (which increases ฯ_AB), or raising the temperature will lead to more frequent collisions.
Examples & Analogies
Think of a busy dance floor. The more people you have there (higher number densities), the more likely they are to bump into each other (collide). If more space is made for dancing (larger collision cross-section), or if the music is faster (higher temperature), the dancers will also collide more often. Each factor contributes to how dynamic and lively the dance floor becomes!
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Effective Collisions: Successful collisions between reactants that lead to formation of products.
-
Steric Factor (p): A measure of how molecular orientation affects the likelihood of an effective collision.
-
Collision Frequency: The rate at which collisions between reactants occur, influenced by concentration and molecular structure.
-
Maxwell-Boltzmann Distribution: Represents the distribution of energies among molecules at a given temperature.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Chemical reactions involving gases typically demonstrate higher reaction rates with increased pressure due to more frequent effective collisions.
-
The reaction between hydrogen and oxygen to form water is considerably faster at higher temperatures due to increased energy and collision frequency.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
๐ต Rhymes Time
-
When molecules collide with great speed, / In the right form, they succeed!
๐ Fascinating Stories
-
Imagine molecules at a dance. Only those in good positions can form pairs and 'react' to create products as the music plays. This emphasizes how orientation matters.
๐ง Other Memory Gems
-
To remember what makes a collision effective: Energy, Orientation, and the Steric Factor (E.O.S.).
๐ฏ Super Acronyms
p = Proper orientation for effective collisions!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Collision Frequency (Z_AB)
Definition:
The number of collisions per unit time per unit volume between two species in a gas.
-
Term: Steric Factor (p)
Definition:
The fraction of collisions that occur with the correct orientation to lead to a reaction.
-
Term: Activation Energy (Ea)
Definition:
The minimum energy required for a successful reaction to occur.
-
Term: MaxwellBoltzmann Distribution
Definition:
A statistical distribution of the energies of particles in a gas at a given temperature.
-
Term: Number Density (N)
Definition:
The number of particles per unit volume.