9. Alternating Current

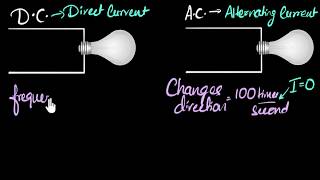
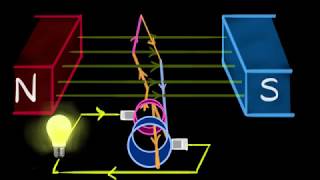
● Alternating Current (AC) is a type of electric current in which the direction and magnitude of the current periodically reverse. ● AC is commonly used in power transmission and most household electrical appliances because it is more efficient for long-distance transmission than direct current (DC). ● In AC, the voltage alternates between positive and negative values over time, producing a sinusoidal wave.

Alternating Current (AC) is distinct from Direct Current (DC) because it periodically changes its direction and intensity. This characteristic makes AC especially effective for transmitting electricity over long distances, as it can be transformed to higher voltages with ease, minimizing energy loss. The sinusoidal wave shape of AC is significant, as it represents the continuous change in voltage levels, oscillating between positive and negative values.

Imagine a roller coaster that rises and falls smoothly; similarly, in AC, the electric current rises to a peak (positive), falls back to zero, dips down to a negative peak, and then returns to zero again, completing one full cycle of the ride. Just as it's more thrilling for the roller coaster to move up and down, AC's ability to reverse direction allows for more efficient use of electrical energy in homes and industries.

● Frequency (f) ● The frequency of an AC signal refers to the number of cycles it completes in one second. ● It is measured in Hertz (Hz), where 1 Hz represents one complete cycle per second. ● In most countries, the standard frequency of AC is 50 Hz or 60 Hz, depending on the region. ● Amplitude ● The amplitude of an AC signal is the maximum value of the current or voltage in the positive or negative direction. ● It represents the peak value of the waveform. ● Period (T) ● The period of an AC wave is the time required to complete one cycle. ● The period is the reciprocal of the frequency: T=1f where T is the period in seconds and f is the frequency in Hz.

Key characteristics of AC include frequency, amplitude, and period. Frequency (measured in Hertz) tells us how many cycles occur each second—commonly 50 Hz or 60 Hz around the world. Amplitude represents the highest level of voltage or current in a cycle, while the period denotes the time it takes for one complete cycle. Understanding these characteristics is crucial for analyzing how AC functions in electrical systems.

Think of a singer producing a sound wave. The frequency would be like the speed of their notes: a faster singer creates higher notes (higher frequency), while a slower one produces lower notes. Amplitude is like the volume of their singing—the louder they are, the higher the amplitude. Just as these qualities define the sound, they also characterize the behavior of AC in circuits.

● Sinusoidal AC Wave ● The most common form of AC is the sinusoidal wave, where the current and voltage vary sinusoidally with time. ● The general mathematical form of a sinusoidal AC wave is: I(t)=Imaxsin(ωt+ϕ) where: ○ I(t) is the instantaneous current at time t, ○ Imax is the peak current (maximum current), ○ ω is the angular frequency (ω=2πf), ○ t is the time, ○ ϕ is the phase angle, which represents the initial displacement of the wave.

The sinusoidal AC wave is characterized by its smooth, repetitive oscillation. The mathematical representation includes the instantaneous current as a function of time, incorporating peak current, angular frequency, and phase angle. Each component impacts how the wave behaves in terms of timing and power delivery in AC systems. This sinusoidal shape is preferred due to its efficiency in generating electric power.

Visualize a wave at the beach rolling in. That smooth rise and fall mirrors the sinusoidal wave’s shape: as the wave comes ashore, it peaks before crashing down, reflecting how the voltage and current oscillate over time in AC. Just as the rhythm of those waves is predictable, the formula helps us predict the behavior of AC in circuits.

● When AC passes through a resistor, the current is in phase with the voltage. The current is directly proportional to the voltage and is calculated using Ohm's Law: IRMS=VRMS/R ● When AC passes through an inductor, the current lags the voltage by 90 degrees (π/2 radians). ● The inductive reactance XL of an inductor is given by: XL=ωL=2πfL ● When AC passes through a capacitor, the current leads the voltage by 90 degrees (π/2 radians). ● The capacitive reactance XC of a capacitor is given by: XC=1/(ωC)=1/(2πfC)

The behavior of AC varies significantly between components: with resistors, the current and voltage are in sync (in phase), while in inductors, the current lags behind voltage, indicating that inductors resist changes in current. Conversely, in capacitors, the current leads the voltage. These relationships are crucial for understanding how energy flows through AC circuits and how these elements react to alternating currents.

Think of a synchronized swimming team. In a resistor, all swimmers move together (in phase), while in an inductor, one swimmer delays their movement, resulting in a lag. In a capacitor, one swimmer takes the lead, showing how each component influences the flow of electric current in different ways. Understanding these dynamics is key in electrical engineering.

--