Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
AC in a Resistor
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's dive into how AC behaves in a resistor. When current flows through a resistor, can anyone tell me the relationship between current and voltage?
I think the current and voltage are in phase, right?
Exactly! The current and voltage are in phase, meaning they reach their maximum and minimum values at the same time. This relationship can be expressed using Ohm's Law. Can anyone recall what the formula is for the RMS current?
Is it I_RMS = V_RMS / R?
Correct! We use this relationship to calculate how much current flows relative to the voltage and resistance. Remember: resistors simply resist current without changing phase.
So, in a resistor, if we increase the voltage, the current scales up directly with it?
Right! Thatβs the linearity of Ohmβs Law in action. Letβs summarize: AC in a resistor means voltage and current are in phase, with the direct relationship expressed by I_RMS = V_RMS / R.
AC in an Inductor
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs explore how AC behaves with inductors. When current passes through an inductor, what happens to the phase of current relative to voltage?
Doesnβt the current lag behind the voltage?
That's correct! The current lags the voltage by 90 degrees. This phase difference indicates that the inductor opposes changes in current flow. Can anyone remind me of the formula for inductive reactance?
It's X_L = 2ΟfL, right?
Exactly right! Inductive reactance shows how much an inductor resists changes in AC. Why is it important to know this?
So we can understand how inductors affect current flow and design effective circuits?
Precisely! So to summarize: AC in an inductor leads to a 90-degree lag in current, calculated using the formula X_L = 2ΟfL.
AC in a Capacitor
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Lastly, let's discuss the impact of capacitors on AC. What happens to the current in relation to voltage when AC passes through a capacitor?
The current leads the voltage by 90 degrees!
Thatβs absolutely right! Capacitors allow current to flow before the voltage reaches its peak. Can anyone tell me the formula for capacitive reactance?
It's X_C = 1/(2ΟfC)!
Nice work! This capacitive reactance indicates how much a capacitor resists current changes in AC. Why might this phase lead be significant in electrical circuits?
It helps us understand timing issues in AC signals, especially in timing circuits!
Exactly! To summarize: AC in a capacitor results in a current that leads the voltage by 90 degrees, characterized by X_C = 1/(2ΟfC).
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section outlines the distinct behaviors of AC when it interacts with resistors, inductors, and capacitors. It emphasizes the in-phase relationship of current and voltage in resistors, the 90-degree lag in inductors, and the 90-degree lead in capacitors. Additionally, it provides formulas to calculate RMS values, reactance, and overall current in circuits with these components.
Detailed
Behavior of AC in a Resistor, Inductor, and Capacitor
This section explores how alternating current (AC) behaves as it flows through different electrical components: resistors, inductors, and capacitors. Understanding these behaviors is crucial for analyzing AC circuits effectively.
AC in a Resistor
When AC flows through a resistor, the current is in phase with the voltage. This means that the current reaches its maximum and minimum values at the same times as the voltage. The relationship between the RMS values of current and voltage is expressed through Ohm's Law:
$$ I_{RMS} = \frac{V_{RMS}}{R} $$
where $I_{RMS}$ is the root mean square current, $V_{RMS}$ is the root mean square voltage, and $R$ is the resistance.
AC in an Inductor
In circuits containing inductors, the current lags behind the voltage by 90 degrees (or Ο/2 radians). This phase difference implies that inductor opposes changes in current. The inductive reactance (which indicates how much the inductor resists changes in current) is given by the formula:
$$ X_L = \omega L = 2\pi f L $$
Here, $L$ is the inductance and $\omega$ is the angular frequency.
AC in a Capacitor
Conversely, when AC flows through a capacitor, the current leads the voltage by 90 degrees (or Ο/2 radians). This means the current reaches its peak before the voltage does. The capacitive reactance is described by:
$$ X_C = \frac{1}{\omega C} = \frac{1}{2\pi f C} $$
where $C$ is the capacitance. These characteristics illustrate the distinct ways AC behaves in resistive, inductive, and capacitive circuits which are essential for engineers and technicians in the field of electricity.
Youtube Videos
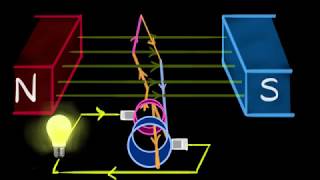
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Behavior of AC in a Resistor
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When AC passes through a resistor, the current is in phase with the voltage. The current is directly proportional to the voltage and is calculated using Ohm's Law:
IRMS=VRMS/R
where IRMS is the RMS current, VRMS is the RMS voltage, and R is the resistance.
Detailed Explanation
In a resistor, Alternating Current (AC) behaves predictably according to Ohm's Law. This law states that the current flowing through a resistor is directly proportional to the voltage across it. When we say that the current is 'in phase' with the voltage, it means that their peaks and troughs occur at the same time. For example, when the voltage is at its maximum, the current is also at its maximum. This relationship allows us to use the RMS (Root Mean Square) values to calculate the current effectively using the formula provided.
In this formula, IRMS represents the effective current flowing through a circuit, VRMS is the effective voltage, and R is the resistance of the component. The use of RMS values is important because AC voltage and current vary sinusoidally, so RMS provides a way to express these values that correlate to continuous DC values.
Examples & Analogies
Think of a simple water pipe system where the resistor is like a section of pipe that restricts water flow. The more water pressure (voltage) you apply, the more water flows through the pipe (current) β as long as the pipe's size (resistance) stays the same. If you increase the pressure, more water flows; if you decrease the pressure, less water flows. The relationship remains constant, like AC through a resistor.
Behavior of AC in an Inductor
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When AC passes through an inductor, the current lags the voltage by 90 degrees (Ο/2 radians). The inductive reactance XL of an inductor is given by:
XL=ΟL=2ΟfL
where L is the inductance, f is the frequency, and Ο is the angular frequency.
Detailed Explanation
In an inductor, the behavior of AC is different from that of a resistor. Here, when AC passes through an inductor, the current does not follow the voltage immediately; it actually lags behind the voltage by 90 degrees. This means that when the voltage reaches its peak, the current is at zero. The inductor creates a magnetic field that stores energy, which causes this lag. The inductive reactance (XL) quantifies the opposition the inductor presents to the AC current, and it's calculated with the formula given, where 'Ο' is the angular frequency derived from frequency 'f' and relates to how fast the AC alternates.
Examples & Analogies
Imagine riding a bicycle. When you want to turn a corner (change the voltage), your bike doesn't turn immediately; thereβs a delay as you correctly lean and navigate the turn (current lagging). Similarly, the inductor needs a moment to adjust to the changing current, resulting in the observed lag compared to the voltage.
Behavior of AC in a Capacitor
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When AC passes through a capacitor, the current leads the voltage by 90 degrees (Ο/2 radians). The capacitive reactance XC of a capacitor is given by:
XC=1/(ΟC)=1/(2ΟfC)
where C is the capacitance, and f is the frequency of the AC signal.
Detailed Explanation
In contrast to inductors, capacitors exhibit a lead in current relative to the voltage when AC flows through them. This means that when the voltage reaches its peak, the current has already peaked earlier, shifting the phase by 90 degrees ahead. The capacitive reactance (XC) describes how much a capacitor resists the flow of AC. This resistance to the change in current depends on both the frequency of the AC signal and the capacitance of the capacitor. Higher frequencies or larger capacitance values decrease XC, making it easier for the current to flow.
Examples & Analogies
Think of a sponge soaking up water. When you pour water (voltage) onto the sponge (capacitor), the sponge absorbs water with a bit of delay because it first fills (current leading). Just as the sponge captures the water more quickly with higher permeability (high frequency), a capacitor allows current to flow more effortlessly with higher frequency AC.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Phase Relationships: In a resistor, current and voltage are in phase; in an inductor, current lags voltage; in a capacitor, current leads voltage.
-
RMS Values: Use of I_RMS and V_RMS to calculate effective current and voltage.
-
Reactance: The opposition offered by inductors (X_L) and capacitors (X_C) to AC.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using Ohm's Law, if V_RMS = 120V and R = 30Ξ©, then I_RMS = 120V / 30Ξ© = 4A.
-
For an inductor with L = 0.5H at 60Hz, the inductive reactance is X_L = 2Ο(60)(0.5) = 188.5Ξ©.
-
For a capacitor with C = 100ΞΌF at 60Hz, the capacitive reactance is X_C = 1/(2Ο(60)(100 x 10^-6)) = 26.53Ξ©.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
In a circuit with L, C, and R, resistors are steady, inductors slow the bar. Capacitors lead, making it quite clear, physics of AC is important, I fear.
π Fascinating Stories
-
Imagine a race among voltage and current; the resistor is the referee ensuring they run together. The inductor is a cautious older friend, lagging behind, while the capacitor is the eager child leading the way. They teach us about how AC behaves differently.
π§ Other Memory Gems
-
RILC: Resistor In Phase, Inductor Lags, Capacitor Leads. This phrase helps remember how AC behaves in each component.
π― Super Acronyms
FOR
- Follows Ohm's Law in Resistor; Opposes in Inductor; Reacts differently in Capacitor.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: RMS Current (I_RMS)
Definition:
The root mean square value of current in an AC circuit, denoting effective current.
-
Term: RMS Voltage (V_RMS)
Definition:
The root mean square value of voltage in an AC circuit, denoting effective voltage.
-
Term: Inductive Reactance (X_L)
Definition:
The opposition to current flow in an AC circuit caused by inductors, measured in ohms.
-
Term: Capacitive Reactance (X_C)
Definition:
The opposition to current flow in an AC circuit caused by capacitors, measured in ohms.
-
Term: Phase Lag
Definition:
The delay of current in relation to voltage in an AC circuit, commonly seen in inductors.
-
Term: Phase Lead
Definition:
The advance of current in relation to voltage in an AC circuit, commonly seen in capacitors.