Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Frequency of AC
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will explore the concept of frequency in alternating current. Frequency refers to how many cycles an AC signal completes in one second. It's measured in Hertz (Hz). Can anyone tell me the common frequencies used in most countries?
Is it 60 Hz in the US and 50 Hz in Europe?
Exactly! You've got it! 60 Hz is standard in the Americas while many other regions use 50 Hz. Remember, frequency is essential because it affects how AC can be used in various applications.
Why does the frequency matter?
Great question! Frequency impacts everything from the functioning of household appliances to the efficiency of power transmission. Longer cycles can mean slower operation for devices.
Let's summarize: Frequency is how many cycles occur per second; it's measured in Hertz, with common standards being 50 Hz and 60 Hz in different parts of the world.
Amplitude and Peak Value
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's dive into amplitude. Amplitude is the maximum value that the voltage or current reaches in an AC cycle. Who can remind us why peak values are important?
Isn't it to determine how much power is delivered?
Exactly! The peak value tells us the maximum power level that the AC can achieve. Also, it influences how we design circuits to handle those high levels without getting overloaded.
So, how do we calculate the RMS value from the peak value?
Excellent inquiry! The RMS value is calculated as the peak value divided by the square root of two. The formula is \( I_{RMS} = \frac{I_{Peak}}{\sqrt{2}} \). This value is crucial for accurately calculating power in AC circuits.
Remember, amplitude gives us the maximum extent of a waveform, and the peak value plays a vital role in energy calculations!
Period and Its Importance
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Moving on, we need to understand the period of an AC wave. The period is the time taken to complete one cycle. Can anyone relate period to frequency?
I think the period is the reciprocal of frequency?
Exactly, fantastic! The period is calculated with the formula T = 1/f, where T is in seconds and f is the frequency in Hertz. It's crucial as it tells us exactly how quickly the waveform repeats.
Why is that significant in real-world applications?
The period helps us design circuits for specific frequencies and ensures that any appliances we use can function optimally at their designated frequencies. It's about matching capabilities!
To sum it up: The period tells us how long it takes for one cycle of AC to complete, and it's essential for matching devices to their power sources.
RMS Value and Calculation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Lastly, let's focus on the RMS value. The effective value of AC is important for practical applications. Can anyone tell me why it's preferable to use RMS for calculations?
Itβs because RMS gives us a more realistic value that can be compared directly to DC values?
That's correct! RMS values allow us to calculate power equivalently as DC power since they provide an effective measure of AC's heating effect.
How do the formulas vary for current and voltage?
Great question! For current, it's \( I_{RMS} = \frac{I_{Peak}}{\sqrt{2}} \), and for voltage, \( V_{RMS} = \frac{V_{Peak}}{\sqrt{2}} \). These formulas are essential when working on real AC circuit calculations.
In summary, RMS values are crucial for accurately determining power, making our understanding of AC much more impactful in electrical engineering.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The characteristics of alternating current (AC) comprise critical concepts such as frequency, measured in Hertz (Hz), amplitude as the peak voltage or current, and period as the duration to complete a cycle. Additionally, understanding peak values and the RMS (Root Mean Square) values is essential, as these metrics are crucial for practical applications in calculating power and energy in AC circuits.
Detailed
Detailed Summary
Characteristics of Alternating Current
Alternating Current (AC) possesses certain distinctive characteristics that distinguish it from Direct Current (DC). These characteristics include:
Frequency (f)
- Frequency is the number of cycles completed in one second, expressed in Hertz (Hz). For example, standard AC frequencies mostly used globally are 50 Hz or 60 Hz.
Amplitude
- The amplitude represents the maximum current or voltage level, demonstrating the peak value in both positive and negative directions of the AC signal.
Period (T)
- The period of the AC wave is defined as the time taken to complete one full cycle and can be calculated using the formula:
T = 1/f, where T is in seconds, and f is frequency in Hz.
Peak Value and RMS Value
- The Peak Value is the maximum instantaneous current or voltage reached during the AC cycle.
- The RMS Value, or Root Mean Square value, is vital as it provides an effective value of the AC signal equivalent to a direct current (DC) that generates the same heat dissipation in a resistor. Formulas for calculating the RMS values are:
- For current: \( I_{RMS} = \frac{I_{Peak}}{\sqrt{2}} \)
- For voltage: \( V_{RMS} = \frac{V_{Peak}}{\sqrt{2}} \)
Understanding these characteristics is essential for efficiently utilizing AC electricity in various applications, especially in power calculations and circuit design.
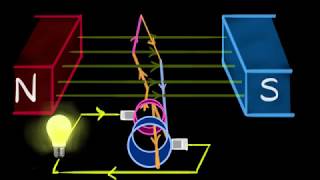
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Frequency (f)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The frequency of an AC signal refers to the number of cycles it completes in one second.
It is measured in Hertz (Hz), where 1 Hz represents one complete cycle per second.
In most countries, the standard frequency of AC is 50 Hz or 60 Hz, depending on the region.
Detailed Explanation
Frequency is a key characteristic of alternating current (AC). It tells us how many times the AC signal completes a full cycle in one second. This is measured in Hertz (Hz). For example, a frequency of 50 Hz means the AC wave goes through 50 complete cycles of alternating current every second. Different countries commonly use frequencies of either 50 Hz or 60 Hz, depending on local electrical standards.
Examples & Analogies
Imagine a Ferris wheel at an amusement park. If the Ferris wheel makes one full rotation every second, it has a frequency of 1 Hz. If it completes 50 rotations in one second, it operates at 50 Hz, just like the frequency of some electrical systems in your home.
Amplitude
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The amplitude of an AC signal is the maximum value of the current or voltage in the positive or negative direction.
It represents the peak value of the waveform.
Detailed Explanation
Amplitude describes how strong the alternating current or voltage is at its greatest point. This peak value is important as it tells us the maximum 'height' of the AC sine wave, which relates to how much current it can deliver to do work, such as powering a light bulb. In AC waveforms, the current and voltage oscillate between positive and negative values, and the amplitude shows the extremes of this oscillation.
Examples & Analogies
Think of amplitude like the height of waves in the ocean. A wave with a high peak (amplitude) can be powerful enough to surf on, just like a higher amplitude in an AC signal would mean it can power more demanding devices.
Period (T)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The period of an AC wave is the time required to complete one cycle.
The period is the reciprocal of the frequency:
T=1/f,
where T is the period in seconds and f is the frequency in Hz.
Detailed Explanation
The period of an AC wave is crucial as it defines how long it takes for one complete cycle of the wave. This period can be calculated using the frequency. If we know the frequency, we find the period by taking the reciprocal of that number. For example, if the frequency is 50 Hz, the period will be T = 1/50 = 0.02 seconds, meaning it takes 0.02 seconds to complete one full cycle.
Examples & Analogies
Picture a runner on a track. If the runner completes one lap (one cycle) in 10 seconds, their period is 10 seconds. If they run faster and complete that lap in 5 seconds, the frequency of their laps increases. Similarly, the faster the AC cycles, the shorter the period.
Peak Value and RMS Value
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Peak Value (IPeak) is the maximum instantaneous value of current or voltage in one cycle.
RMS (Root Mean Square) Value is the effective value of an AC signal, which is equivalent to the value of a DC current that would produce the same heating effect in a resistor.
The RMS value is used in practical applications to calculate power and energy in AC circuits.
Detailed Explanation
The peak value of an AC signal represents the highest point it reaches during its cycle. However, since AC current fluctuates, we also use the Root Mean Square (RMS) value to understand its effective power usage. The RMS value helps us know what the equivalent DC current would be that produces the same amount of heat in a resistor. Itβs important in real-world applications for calculating power and energy.
Examples & Analogies
Imagine using a water hose. The peak pressure in the hose would be like the peak current in an AC signal. But to understand how much water reaches the garden effectively, you'd consider not just that peak but the overall flow - much like how the RMS value tells us how much 'effective power' the AC current can deliver over time.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Frequency: The number of cycles per second measured in Hertz (Hz).
-
Amplitude: The maximum value of current/voltage in an AC signal.
-
Period: The time required to complete one cycle (T = 1/f).
-
Peak Value: Maximum instantaneous value of current/voltage.
-
RMS Value: Effective value of AC that indicates the heat production equivalent to DC.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An AC voltage waveform has a peak voltage of 170V. Its RMS voltage would be approximately 120V, calculated as 170V/β2.
-
If an AC signal has a frequency of 60 Hz, its period would be T = 1/(60) = 0.01667 seconds.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
In alternating current, waves do sway, at 50 or 60 Hertz, they'll play.
π Fascinating Stories
-
Imagine a party where each beat represents a cycle of current. The faster the beat, the higher the frequency, making everyone dance quicker!
π§ Other Memory Gems
-
For remembering peak and RMS: 'Peak is the height that wonβt last; RMS is the average of the waveform cast.'
π― Super Acronyms
AMP for Amplitude, Max value, Peak; remember, RMS is the effective peak you seek.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Frequency
Definition:
The number of cycles per second of an AC signal, measured in Hertz (Hz).
-
Term: Amplitude
Definition:
The maximum value of current or voltage in a sine wave, representing the peak of the waveform.
-
Term: Period
Definition:
The time required to complete one full cycle of an AC wave, calculated as the reciprocal of frequency.
-
Term: Peak Value
Definition:
The maximum instantaneous value of current or voltage reached during a cycle of AC.
-
Term: RMS Value
Definition:
Root Mean Square Value; the effective value of an AC signal that produces the same heating effect as DC.