Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Identifying the Greatest Common Factor
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we'll discuss how to factor polynomials using the greatest common factor, or GCF. Who can tell me what they think a greatest common factor is?
I think it's the largest number that divides all numbers in a set.
Exactly! For polynomials, it also involves variables. Let's say we have the expression 6x^2 + 9x. Can anyone identify the GCF?
Is it 3x?
Correct, the GCF is 3x! Now, let's factor it out. If I factor 3x out of 6x^2 + 9x, what will the expression look like?
It would be 3x(2x + 3)!
Well done! Remember, when factoring out the GCF, we rewrite the expression in the product form.
Practice with GCF
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's practice identifying GCF with another expression: 15y^3 + 10y^2. Who wants to try this one?
I think the GCF is 5y^2.
Good job! So, if we factor out 5y^2, what do we get?
We get 5y^2(3y + 2).
Exactly! Make sure to always verify your GCF is correct by distributing it back. Now, could you all try factoring 12a^2b + 16ab^2 on your own?
Application in Problem-Solving
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
How can factoring by common factors help us beyond just simplifying expressions?
It can help us solve equations quicker!
Exactly! For example, if we factor 2x^2 - 8x, we can quickly see that it can help us find the roots. Can anyone factor that for me?
2x(x - 4)!
Great! Now we can set each factor to zero to find the roots. See how this technique streamlines the process?
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we explore the technique of factorization by common factors. We learn how to identify and extract the GCF from polynomial expressions in order to simplify them, establishing a foundational skill for more complex factorization methods.
Detailed
Factorization by Common Factors
In algebra, factorization is a crucial skill used to simplify expressions and solve equations. One method of factorization is by using the Greatest Common Factor (GCF). This section outlines the process of identifying the GCF from a set of terms in an expression and demonstrates how to factor it out.
Key Points:
- Definition of GCF: The GCF of a set of numbers (or terms) is the largest number (or term) that divides each of them without leaving a remainder. For polynomial expressions, identifying the GCF involves looking for the highest common factor in the coefficients and the lowest power of variables.
- Extracting the GCF: Once the GCF is determined, it is factored out of the expression, resulting in a simplified expression written in a product form.
- Significance in Algebra: Understanding how to factor polynomials is vital in solving equations, simplifying expressions, and applying identities in algebra. This skill sets the groundwork for more advanced topics, including factorization by identities and grouping.
In summary, mastering the technique of factorization by common factors is essential for success in algebra, enabling students to approach more complex expressions with confidence.
Youtube Videos
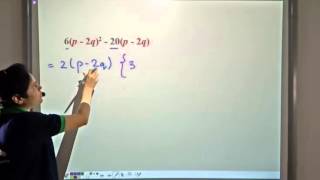
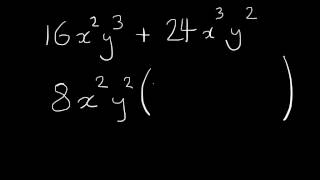
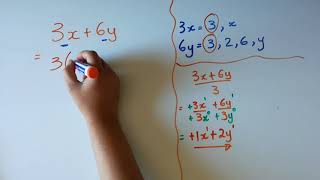
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Common Factors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Extracting the greatest common factor from algebraic expressions.
Detailed Explanation
Factorization by common factors involves finding the largest factor that is common to all terms in an algebraic expression. This process helps simplify expressions, making them easier to work with. The steps for extracting the greatest common factor (GCF) are as follows:
1. Identify the terms of the expression.
2. Determine the factors of each term.
3. Find the greatest factor that appears in all terms.
4. Factor out the GCF from the expression.
For example, in the expression 6xΒ² + 9x, the GCF is 3x, allowing us to rewrite the expression as 3x(2x + 3).
Examples & Analogies
Imagine you are packing items into boxes. The greatest common factor is like the largest box that can fit a certain number of items from different groups. If you have boxes with 6 apples and 9 oranges, the largest box that can hold both types is one that holds 3 fruits. By grouping items in a common box, it becomes easier to organize and transport them.
Step-by-Step Factorization Example
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For instance, consider the expression 12x^3 + 8x^2. The GCF here is 4x^2.
Detailed Explanation
Let's break down the factorization of the expression 12xΒ³ + 8xΒ² step by step:
1. List the coefficients: The coefficients are 12 and 8. The factors of 12 are 1, 2, 3, 4, 6, and 12; for 8, they are 1, 2, 4, and 8.
2. Identify the GCF of the coefficients, which is 4.
3. Identify the variable part. The least power of x in both terms is xΒ².
4. Combine the GCF of the coefficients (4) with the variable part (xΒ²), giving us GCF = 4xΒ².
5. Factor out the GCF: This results in 4xΒ²(3x + 2).
Examples & Analogies
Think of it like distributing fruits among friends. If you have 12 apples and 8 oranges, you want to share them in an organized manner. The GCF helps you figure out the biggest number of friends with whom you can evenly distribute both types of fruits. In this case, each friend gets 4 pieces, and you end up with 3 apples and 2 oranges per friend.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Greatest Common Factor: The largest term that can factor out from all terms in a polynomial.
-
Factorization: The process of expressing a polynomial as a product of its factors.
-
Polynomials: Expressions with variables raised to whole number powers.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Factor 8x^3 + 4x^2. The GCF is 4x^2, and the factored form is 4x^2(2x + 1).
-
Example 2: Factor 15y^3 + 25y^2. The GCF is 5y^2, and the factored form is 5y^2(3y + 5).
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
To factor with ease, find the GCF first,
π Fascinating Stories
-
Imagine a hero who always looked for the biggest tree in the forest, representing the GCF, to lead others safely through the woods of numbers.
π§ Other Memory Gems
-
GCF: Gather Common Factors, which means check what all terms have in common!
π― Super Acronyms
GCF - Greatest Common Factor
- Get Common Fact!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Greatest Common Factor (GCF)
Definition:
The largest number or term that divides all terms in a polynomial expression.
-
Term: Factorization
Definition:
The process of breaking down an expression into a product of its factors.
-
Term: Polynomial
Definition:
An algebraic expression consisting of variables and coefficients combined using addition, subtraction, and multiplication.