Factorization Using Identities
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Algebraic Identities
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Welcome, class! Today, we will dive into factorization using identities. Can anyone tell me why algebraic identities are important?

They help simplify expressions and make them easier to factor!

Exactly! They provide shortcuts to factor complex polynomials. For instance, the identity (a + b)² helps us expand but can also reverse to factor. Does anyone remember how we express this identity?

(a + b)² = a² + 2ab + b².

Great! Now, can someone give an example of when we would use this identity for factorization?

If I see an expression like x² + 6x + 9, I can identify it as a perfect square!

Exactly right, Student_3! It factors to (x + 3)². Remember, identifying these forms is key.

Let's summarize: Algebraic identities simplify expressions and allow for quicker factorization. Be mindful of how they can be rearranged!
Using Identities for Factorization of Common Cases
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s look at more examples! Who knows how we could factor x² - 16?

That's a difference of squares! It factors to (x - 4)(x + 4).

Correct! The identity a² - b² = (a - b)(a + b) is very useful here. How about if we had x² + 10x + 25?

That's also a perfect square! It factors to (x + 5)².

Excellent, Student_1! Recognizing perfect squares and using identities makes this straightforward. Can we discuss any other expressions that look tricky?

What about if we have x³ - 8?

Great question! That would use the identity for a difference of cubes: a³ - b³ = (a - b)(a² + ab + b²). Can we apply that?

So x³ - 2³ factors to (x - 2)(x² + 2x + 4).

Exactly! Understanding various identities is key to effective factorization.
Practice and Application
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s practice! Can someone factor x² - 12x + 36?

That looks like a perfect square: (x - 6)².

Excellent job! Remember to always look for those patterns. What about x² - 6x + 9?

(x - 3)².

Correct! Now let's try something new: how would we factor 2x² + 8x?

We can factor out the greatest common factor, 2x, so it becomes 2x(x + 4).

Wonderful! Factor by grouping and finding common factors are also part of this process. Who can summarize what we learned today?

We learned how to use algebraic identities to quickly factor expressions.

Exactly! Keep practicing these identities, and they will greatly simplify your work.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Factorization using identities involves utilizing standard algebraic identities such as the square of a sum, square of a difference, and others to factorize polynomials quickly. This method simplifies the factorization process by providing a straightforward approach to breaking down complex expressions into their manageable components.
Detailed
Factorization Using Identities
This section explores the concept of factorization through the lens of algebraic identities, which are equations that hold true for all values of the variables involved. The primary aim here is to enable students to understand how these identities can simplify the factorization process of polynomials.
Key Algebraic Identities
Understanding the following algebraic identities is crucial for factorization:
- (a + b)² = a² + 2ab + b²
- (a - b)² = a² - 2ab + b²
- a² - b² = (a - b)(a + b)
- (a + b)³ = a³ + 3a²b + 3ab² + b³
- (a - b)³ = a³ - 3a²b + 3ab² - b³
These identities can be employed to factor expressions efficiently. For example, if we have an expression like x² - 9, we can recognize it as a difference of squares, which can be factored as (x - 3)(x + 3) using the identity a² - b² = (a - b)(a + b).
This section aims not just to teach the identities, but also to create a solid mental framework for recognizing when and how to apply them in various polynomial expressions, enhancing students' problem-solving skills in algebra.
Youtube Videos
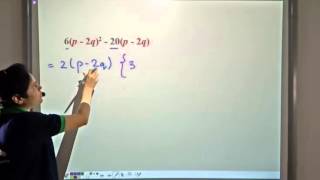

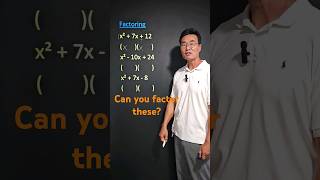



Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Factorization Using Identities
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Applying algebraic identities to factorize expressions efficiently.
Detailed Explanation
Factorization using identities involves recognizing and utilizing standard algebraic identities to rewrite and simplify expressions. Instead of expanding an expression as in multiplication, factorization helps us express that same mathematical entity as a product of simpler expressions, making it easier to work with. For example, when we have an expression like (a + b)², instead of calculating it directly by expanding, we can use the identity to rewrite it as a² + 2ab + b².
Examples & Analogies
Consider baking a cake. Instead of viewing the whole cake (the expression) and wondering about its ingredients (the factored form), if you had a recipe (the algebraic identity), you could easily list out the component ingredients to recreate or adjust your cake. This is similar to how algebraic identities allow us to piece together complex expressions into manageable factors.
Examples of Algebraic Identities for Factorization
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- (a+b)² = a² + 2ab + b²
- (a−b)² = a² − 2ab + b²
- a² − b² = (a−b)(a+b)
- (a+b)³ = a³ + 3a²b + 3ab² + b³
- (a−b)³ = a³ − 3a²b + 3ab² − b³
Detailed Explanation
These are important algebraic identities that can be used for factorization. For example, consider the identity a² − b² = (a − b)(a + b). If we have an expression like 9 − 4, we can recognize 9 as 3² and 4 as 2². Using the identity, we can write it as (3 − 2)(3 + 2), which simplifies to 1 × 5 = 5. This demonstrates how we can factorize expressions using known identities.
Examples & Analogies
Imagine you have a rectangular garden. If you know the length and width (the original expression), you can find the area by multiplying the two dimensions. Similarly, when we factorize, we are essentially finding different ways to break down that area into manageable parts. Using our identities is like having the measurements on a blueprint that shows how to rearrange the garden beds effectively.
Application of Identities in Complex Expressions
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Using identities helps to simplify the expressions, especially when they appear in more complex forms.
Detailed Explanation
In more complex expressions, recognizing patterns that match the algebraic identities is crucial for simplification. For instance, if you encounter an expression such as a²x² + 2abx + b², you can factor it as (ax + b)² by identifying it fits the form of the (a + b)² identity. This technique can significantly reduce computational efforts and clarify calculations, especially in polynomial equations.
Examples & Analogies
Think of solving a jigsaw puzzle. Each piece (the complex term) has to find its right place to complete the picture (the entire expression). Recognizing pieces that fit together (using identities) can make assembling the puzzle much quicker and easier, rather than forcing pieces that don’t quite match.
Key Concepts
-
Factorization: The process of breaking down an expression into its multiplicative components.
-
Algebraic Identities: Standard equations like (a + b)² that help simplify polynomial factorization.
-
Difference of Squares: A key identity that states a² - b² = (a - b)(a + b), crucial for factorization.
-
Perfect Squares: Expressions like (a + b)² can be factored directly into their square form.
Examples & Applications
Example 1: Factor x² - 25 using the difference of squares: x² - 5² = (x - 5)(x + 5).
Example 2: Factor x² + 6x + 9 using the perfect square identity: (x + 3)².
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Squares of numbers, be aware, factor them with utmost care.
Stories
Once there was a polynomial who couldn't find its factors until it met its identity friends, who showed it how to break down easily!
Memory Tools
F.O.R.M. - For One Rational Man, always remember factorization patterns!
Acronyms
P.A.C.E. - Perfect squares Always Create Easy factors.
Flash Cards
Glossary
- Algebraic Identity
An equation that holds true for all values of the variables involved.
- Difference of Squares
A special case of an algebraic identity where the expression can be factored as (a - b)(a + b).
- Perfect Square
An expression that can be written as the square of a binomial, e.g., (a + b)².
- Common Factor
A factor that is common to all terms in a polynomial, which can be factored out.
Reference links
Supplementary resources to enhance your learning experience.
