Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Factorization by Grouping
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we are going to learn about factorization by grouping, a valuable technique for simplifying polynomials. Can someone tell me what factorization means?
Factorization is when we express a number or an expression as a product of its factors.
Exactly! It allows us to simplify or solve expressions easier. Now, can anyone give me an example of a polynomial we might want to factor?
How about xΒ² + 5x + 6?
Good example! Instead of directly factoring this, we could use grouping to rearrange or group terms effectively. Let's remember our acronym 'GCF': Group, Common Factor, Factor.
So, we first group terms?
That's correct! Let's continue exploring that.
Demonstrating Factorization by Grouping
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs take a polynomial: ax + bx + ay + by. Can anyone suggest how you would start grouping these terms?
We can group them as (ax + ay) and (bx + by).
Exactly! Now, can someone tell me the next step?
We factor out the common factors in each group?
Right! By factoring, we get 'a(x + y) + b(x + y)'. What can we do next?
We can factor out (x + y) from the expression.
Very well! So, weβve simplified our expression to (x + y)(a + b). Great teamwork!
Practical Applications and Examples
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we've practiced the technique, can anyone think of why factorization by grouping might be useful in real life?
It helps in simplifying equations, which could be applied in area calculations or profit analysis in business!
Yeah, it can help break down problems into smaller, more manageable parts.
Absolutely! The clearer we can make a complex polynomial, the easier it is to see solutions or applications.
Can we have another example using bigger numbers?
Great idea! Let's examine 6xΒ² + 15x + 6y + 15y next.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section covers the method of factorization by grouping, which is useful in simplifying complex polynomials by organizing terms into groups that share common factors, making them easier to factor.
Detailed
Factorization by Grouping
Factorization by grouping is a powerful technique used to simplify more complex expressions, particularly polynomials. The goal is to rearrange the terms of a polynomial into groups that can be easily factored. This technique is especially useful when dealing with polynomials that do not appear to have a clear common factor at first glance.
Key Points
- Understanding the Method: Factorization by grouping helps break down polynomials by grouping terms in pairs or sets that can share a common factor. For example, in the polynomial expression ax + ay + bx + by, one may group (ax + ay) and (bx + by), leading to a further simplification.
- Recognizing Suitable Terms: Not all polynomial expressions can be directly subjected to grouping. Students should learn to identify terms that effectively yield common factors.
- Application of Common Factor Extraction: After grouping, students will apply the extraction of common factors to each group, revealing simpler components of the original polynomial.
Thus, mastering factorization by grouping is pivotal as it lays the groundwork for advanced algebra topics and methods used in solving polynomial equations.
Youtube Videos
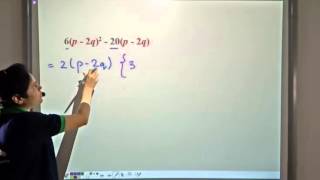
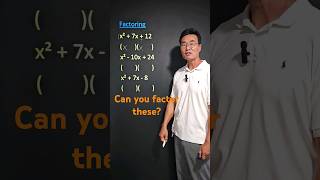
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Factorization by Grouping
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Factorization by grouping involves arranging terms in a polynomial into groups and then factoring out the common factors from each group.
Detailed Explanation
Factorization by grouping is a technique used when dealing with polynomials that have four or more terms. The first step is to rearrange the terms into pairs or groups. Once grouped, we look for common factors within each group, which makes the expression easier to manage. This method is particularly useful when you cannot factor the polynomial as a whole or when direct observation of common terms is not evident.
Examples & Analogies
Think of factorization by grouping like organizing your closet. If you have various clothes scattered everywhere, grouping similar items togetherβlike jeans with jeans and shirts with shirtsβhelps in making the closet tidy. Similarly, by grouping terms in a polynomial, we can find common factors which help us simplify the expression.
Step-by-Step Process
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Group the terms into pairs or suitable clusters.
- Factor out the common factor from each group.
- Combine any common binomials that emerge from the groups.
- Write the final factorized form.
Detailed Explanation
To effectively use the factorization by grouping method, follow these steps: First, review the polynomial and decide how to group the terms meaningfully. For instance, for the polynomial a + b + ac + bc, you might group (a + b) and (ac + bc). Next, factor out the common elements from each group, such as taking out 'a' from the first group and 'c' from the second, which leads to a grouping of (1)(a + b) + (c)(a + b). Finally, look for a common binomial factor that can be factored out, leading to (a + b)(1 + c) as the end result.
Examples & Analogies
Consider factorizing a shopping list. If you have items like apples, oranges, bread, and milk, you can group fruits (apples and oranges) and dairy (bread and milk). By separating them, you can identify how many items belong to each category, making the shopping task more straightforward, similar to how we combine common factors in polynomials.
Example of Factorization by Grouping
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For example, consider the polynomial x^3 + 3x^2 + 2x + 6.
1. Group the terms: (x^3 + 3x^2) + (2x + 6).
2. Factor out the common factors: x^2(x + 3) + 2(x + 3).
3. Notice the common binomial (x + 3): (x + 3)(x^2 + 2).
Detailed Explanation
Let's break down this example step-by-step: Start with the polynomial x^3 + 3x^2 + 2x + 6. To use factorization by grouping, group the first two terms and the last two terms. Factor x^2 from the first group, and 2 from the second. Both groups will yield a common factor of (x + 3). After this step, you're left with the expression (x + 3)(x^2 + 2). This is a clear illustration of how grouping facilitates factoring more complex polynomials.
Examples & Analogies
Imagine a team working on a project where they need to present two partsβresearch and findings. Grouping the research together and the findings together allows team members to focus on consolidating their work rather than getting lost in disparate parts. Similarly, in factorization, grouping helps us organize the polynomial so we can collaborate to find the factors.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Factorization by Grouping: A technique to simplify polynomials by grouping terms.
-
Common Factors: Factors that are shared by different terms in a polynomial.
-
Rearranging Terms: The process of organizing polynomial terms into pairs or groups for easier factorization.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: Factor 2xy + 4x + 3y + 6 using grouping. Group terms as (2xy + 4x) + (3y + 6) and then factor out common factors.
-
Example 2: Factor x^2 + 3x - 4 using grouping. Group as (x^2 + 4x) - (1x + 4).
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Group the terms with care, find their common share!
π Fascinating Stories
-
Once upon a time, in an algebra land, there lived polynomials that were too complex. They invited their neighboring terms to form groups, and together they split into simpler products!
π§ Other Memory Gems
-
GCF: Group, Common Factor, Factor! Remember this to conquer polynomial fractions.
π― Super Acronyms
F.G.F.
- Factor
- Group
- and Find the common elements in polynomial roots.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Factorization
Definition:
The process of expressing an algebraic expression as a product of its factors.
-
Term: Grouping
Definition:
A method of rearranging terms in an expression to find common factors.
-
Term: Common Factor
Definition:
A factor that is shared by two or more terms.