Fourier Integral Formula
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the Need for Fourier Integrals
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to discuss the importance of Fourier Integrals, which allow us to handle non-periodic functions. Can anyone recall why Fourier Series work best for periodic functions?

Because Fourier Series break down periodic functions into sums of sines and cosines?

Exactly! Now what if we have a function that doesn’t repeat, like a temperature change over time? That's where Fourier Integrals shine.

So, they help in scenarios that are not periodic?

Right! They allow us to express non-periodic functions as continuous sums of sine and cosine waves.
Deriving the Fourier Integral
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s dive into how we derive the Fourier Integral from the series. Can anyone recall the Fourier Series representation?

It's the sum of sines and cosines over a specific interval.

And what happens when our domain goes to infinity? How does that change things?

The coefficients become continuous, and you switch from a sum to an integral.

Correct! So we move from sums to integrals, resulting in the Fourier Integral representation. Can anyone state the main formula?

$$ f(x) = \int_0^{\infty} [A(\omega) \cos(\omega x) + B(\omega) \sin(\omega x)] d\omega $$

Well done! This is crucial for solving real-world problems in engineering.
Applications of the Fourier Integral
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let’s discuss specific applications of Fourier Integrals. What areas in Civil Engineering could benefit from this method?

Heat conduction problems?

Absolutely! Fourier Integrals help solve heat distribution in structures. What about another example?

Maybe vibration analysis for beams?

Exactly! They are essential in analyzing how materials respond to dynamic loads. Can anyone summarize the main benefits?

They're good for non-periodic scenarios and help with transient phenomena!

Great summary! These applications demonstrate the practical significance of Fourier Integrals in engineering.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section introduces the Fourier Integral Formula, which allows for the representation of non-periodic functions using continuous superpositions of sine and cosine functions. It emphasizes the conditions under which these integrals can be applied, the derivation of the formula, and its significance in areas such as civil engineering.
Detailed
Fourier Integral Formula
The Fourier Integral Formula allows us to represent a piecewise continuous and absolutely integrable function, f(x), defined on the entire real line, as a continuous integral of sines and cosines or complex exponentials. Given the necessary conditions, such as the absolute integrability over the domain (-∞, ∞), we can express the function using:
Basic Formula
$$ f(x) = \int_0^{\infty} [A(\omega) \cos(\omega x) + B(\omega) \sin(\omega x)] d\omega $$
Where:
- $$ A(\omega) = \frac{1}{\pi} \int_{-\infty}^{\infty} f(t) \cos(\omega t) dt$$
- $$ B(\omega) = \frac{1}{\pi} \int_{-\infty}^{\infty} f(t) \sin(\omega t) dt.$$
Alternatively, this function can also be described using the complex Fourier integral:
$$ f(x) = \frac{1}{2\pi} \int_{-\infty}^{\infty} f_b(\omega)e^{i\omega x} d\omega $$
Where the Fourier transform ($$f_b(\omega)$$) is defined as:
$$ f_b(\omega) = \int_{-\infty}^{\infty} f(t)e^{-i\omega t} dt $$
This formulation is fundamental in engineering applications, allowing for the analysis of transient phenomena and non-periodic boundary conditions. Fourier integrals play a crucial role in solving heat conduction problems, vibration analysis, and various dynamic analyses in civil engineering.
Youtube Videos
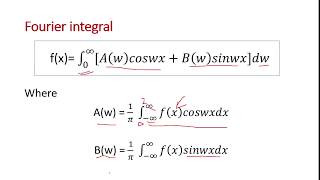








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Conditions for Fourier Integral
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let f(x) be a function such that:
- f(x) is piecewise continuous on (−∞,∞)
- f(x) is absolutely integrable over (−∞,∞)
Detailed Explanation
For a function f(x) to be expressed using the Fourier Integral, it must meet specific conditions. First, being 'piecewise continuous' means that the function can have jumps or breaks, but it must be piecewise smooth and should not have infinite discontinuities. Second, 'absolutely integrable' means that when you take the integral of the absolute value of the function across the entire real line (-∞ to +∞), the result should be finite. This ensures that the function doesn't blow up to infinity, making it manageable for analysis.
Examples & Analogies
Think of these conditions like preparing a cake (the Fourier Integral). You need good quality ingredients (continuous and integrable functions). If your ingredients are spoiled (like having infinite discontinuities or being non-integrable), the resulting cake will be ruined. Only when both criteria are met can you bake successfully.
Fourier Integral Representation
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Then,
Z ∞
f(x)= [A(ω)cos(ωx)+B(ω)sin(ωx)] dω
0
Where:
1 Z ∞ 1 Z ∞
A(ω)= f(t)cos(ωt)dt, B(ω)= f(t)sin(ωt)dt
π π
−∞ −∞
Detailed Explanation
The Fourier Integral gives us a way to represent the function f(x) using an integral that combines both cosine and sine functions. The terms A(ω) and B(ω) represent the coefficients that determine how much each cosine and sine wave contributes to the overall shape of the function f(x). Specifically, A(ω) and B(ω) are calculated by integrating f(t) multiplied by cos(ωt) and sin(ωt) respectively, over all values from -∞ to ∞, normalized by π.
Examples & Analogies
Imagine you are trying to reconstruct a complex sound from its individual notes. Each note corresponds to the cosine and sine waves that make up the sound you hear. The functions A(ω) and B(ω) are like the strength of each note; by combining them properly, you can recreate the original sound, just like how the integral provides a complete picture of the original function.
Complex Form of Fourier Integral
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Alternatively, combining cosine and sine terms, we can express the function using the complex Fourier integral:
1 Z ∞
f(x)= fb(ω)eiωxdω
2π
−∞
Where:
Z ∞
f b(ω)= f(t)e−iωtdt
−∞
Detailed Explanation
The complex Fourier integral is a compact and elegant way to represent the Fourier Integral. In this form, fb(ω) represents the Fourier transform of the function f(x), which essentially captures the frequency content of the function in the complex domain. The eiωx term incorporates both sine and cosine in a single expression. This formulation simplifies calculations and allows for more sophisticated mathematical manipulation.
Examples & Analogies
Think of the complex form as a high-quality camera that captures not just images (the function) but adds depth and dimension (frequency content). It gives a more comprehensive view that combines all essential details in one shot, making it easier for engineers and scientists to analyze and manipulate information.
Key Concepts
-
Fourier Integral: A way to represent non-periodic functions as a continuous sum of sines and cosines.
-
Conditions for Fourier Integrability: Piecewise continuity and absolute integrability are necessary for valid representation.
-
Applications in Engineering: Fourier integrals are particularly useful for heat conduction, vibration analysis, and other non-periodic phenomena.
Examples & Applications
The Fourier Integral Formula can be applied to model temperature distribution in a beam subjected to instantaneous heating.
Vibrational response of beams or structures can be analyzed using Fourier integrals to determine stress distribution over time.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
For every wave that does not repeat, Fourier's functions make it neat.
Stories
Imagine a bridge that sways with the breeze. Fourier's integrals help civil engineers see what happens in times like these.
Memory Tools
P.A.I.R: Piecewise, Absolutely Integrable, Required for Fourier.
Acronyms
F.I.R.E
Fourier Integral Representation of Engineering.
Flash Cards
Glossary
- Fourier Integral
A mathematical expression that represents a non-periodic function as a continuous sum of sines and cosines.
- Piecewise Continuous
A function that is continuous except for a finite number of points where it is allowed to be discontinuous.
- Complex Fourier Integral
An alternate representation of the Fourier integral using complex exponentials.
- Absolutely Integrable
A function for which the integral of its absolute value over its entire domain is finite.
Reference links
Supplementary resources to enhance your learning experience.
