Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fourier Series
Unlock Audio Lesson
Alright class, let's start with Fourier Series. It's a method to express functions defined on a finite interval using sines and cosines. Can anyone tell me what that means?
Does it mean we can break down any periodic function into simpler parts?
Exactly! The series expands the function into infinite sums of sine and cosine terms. Remember, we can represent f(x) as an infinite sum of these terms.
But what about non-periodic functions?
Great question! That's where Fourier Integrals come in. They'll help us represent functions when the period of the function is infinite.
So, is it like changing from sums to integrals?
Yes! As we move towards an infinite domain, the coefficients from the Fourier series transition into continuous variables, leading to integrals.
In summary, Fourier Integrals are crucial for dealing with engineering problems involving non-periodic conditions.
Context of Non-Periodic Functions
Unlock Audio Lesson
Now let's discuss why Fourier Integrals are necessary. Civil engineering often involves phenomena like vibrations in structures or heat conduction, which aren't restricted to periodic behavior.
So, these problems can change over time or in response to different conditions, right?
Exactly! For instance, if we're analyzing heat transfer in a rod after an instantaneous heat source, the conditions can change rapidly, hence we require Fourier Integrals.
I see, so the integrals give us a more fluid representation of these changes?
That's correct! They allow us to model these transient behaviors more appropriately.
In summary, Fourier Integrals provide the flexibility needed in situations where functions are non-periodic.
Transition from Fourier Series to Fourier Integrals
Unlock Audio Lesson
Let's dive deeper into the transition from Fourier Series to Fourier Integrals. When we have a Fourier Series of f(x) on a finite interval, as L approaches infinity, we see a transformation happen.
What does this transformation look like?
As n approaches infinity, the discrete sums of sines and cosines convert into integrals, enabling us to express non-periodic functions using integrals instead of sums.
So it's like taking the limit of the series as we extend our interval to infinity?
Right! This leads to expressions involving continuous variables rather than discrete coefficients.
Can we summarize the difference between the two?
Certainly! Fourier Series deals with periodic functions over a finite interval, while Fourier Integrals handle non-periodic functions over an infinite interval.
In conclusion, understanding this transition opens the door to applying these concepts in practical scenarios.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Fourier Integrals extend the principles of Fourier Series to non-periodic functions, providing a method to represent them as continuous sums of sines and cosines. This is crucial for solving various engineering problems, especially those with non-periodic boundary conditions.
Detailed
The Need for Fourier Integrals
In practical applications, especially in fields such as Civil Engineering, many phenomena such as heat conduction, structural vibrations, and signal transmission are best described by functions that are not periodic. Fourier Series effectively represent periodic functions but become inadequate for non-periodic functions.
To address this limitation, Fourier Integrals provide a solution by allowing non-periodic functions to be articulated as a continuous superposition of sines and cosines (or exponential functions). This mathematical transition occurs as the interval of consideration tends towards infinity (L → ∞), leading to the representation of these functions through integrals rather than sums.
In essence, the Fourier Integral becomes an essential tool for solving engineering problems that exhibit non-periodic boundary conditions and transient phenomena, enabling engineers to analyze systems more effectively.
Youtube Videos
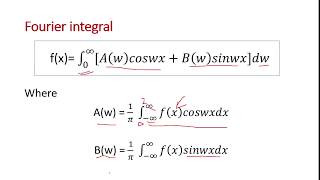
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Fourier Series
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Fourier Series represents a function f(x) defined on a finite interval [−L,L] as an infinite sum of sines and cosines:
f(x)=
a_0 + Σ (a_n cos(nπx/L) + b_n sin(nπx/L)), where n = 1 to ∞.
Detailed Explanation
Fourier Series allow us to express periodic functions using a sum of sine and cosine functions. For any function f(x) defined over a finite interval of length 2L, we can decompose it into a series where each term is based on sine and cosine functions adjusted by coefficients a_n and b_n. The coefficients are calculated to make the sum closely match or equal the original function over this interval.
Examples & Analogies
Imagine trying to recreate a complicated musical tune (the function f(x)) using just a series of basic notes (sines and cosines). By adjusting the volume of each note through the coefficients (a_n and b_n), you can get closer and closer to the original tune.
Limitations of Fourier Series
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
But for non-periodic functions or when the interval becomes infinitely large (L→∞), the discrete nature of the Fourier coefficients becomes continuous, and the sum becomes an integral.
Detailed Explanation
While Fourier Series work great for periodic functions, they struggle with non-periodic functions or when the function is defined over an infinite domain. When we try to extend this idea beyond a finite range or if the function doesn't repeat, the coefficients that would normally make the series discrete become continuous values. This transition is critical to defining Fourier Integrals, where we express non-periodic functions as integrals rather than sums.
Examples & Analogies
Think about using a light bulb to see everything in a room (Fourier series). It works well if the room is closed off (a finite interval), but imagine trying to illuminate a vast, open field (an infinite interval) using the same method. You would need a different approach to cover all areas, similar to how we move from sums to integrals in non-periodic scenarios.
Introduction to Fourier Integrals
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This transition leads us to Fourier Integrals, which allow us to express non-periodic functions as a continuous superposition of sines and cosines (or exponential functions).
Detailed Explanation
Fourier Integrals generalize the concept of Fourier Series. They allow us to represent any non-periodic function as a continuous combination of sine and cosine functions. By integrating over a continuous range, we can handle functions that do not fit neatly into the periodic framework of Fourier Series, thus extending the applicability of Fourier analysis into a broader domain.
Examples & Analogies
Imagine you are mixing different colors of paint to create a new shade (a non-periodic function). Instead of using only a finite selection of colors (limited sums), you mix an unlimited variety of shades in different amounts (continuous integration), leading to a vast range of possible new colors, just like we use Fourier Integrals to achieve a wider variety of function representations.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Transition from sums to integrals in Fourier analysis.
-
Importance of Fourier Integrals in non-periodic conditions.
-
Representation of non-periodic functions using continuous terms.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Temperature distribution in a rod following an instantaneous heat source.
-
Vibration analysis for structures subject to varying loads.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Fourier's Integrals we embrace, for functions with no periodic pace.
📖 Fascinating Stories
-
Imagine a civil engineer dealing with a bridge. When the wind blows, it doesn’t follow a set rhythm. Fourier Integrals help describe how the bridge vibrates under this unpredictable force.
🧠 Other Memory Gems
-
For functions without ends, use Fourier’s friends: Integrals do blend!
🎯 Super Acronyms
FINE
- Functions Integrating Non-Periodic Expressions.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fourier Series
Definition:
A representation of a periodic function as an infinite sum of sines and cosines.
-
Term: Fourier Integral
Definition:
An expression of a non-periodic function as an integral of sine and cosine functions.
-
Term: Piecewise Continuous Function
Definition:
A function that is continuous on finite intervals with a finite number of discontinuities.
-
Term: Absolutely Integrable Function
Definition:
A function for which the integral of its absolute value over its entire domain is finite.