Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fourier Integrals
Unlock Audio Lesson
Today, we will explore the concept of Fourier integrals and their application in engineering problem solving. Can anyone tell me what a Fourier integral is?
Isn't it used to represent non-periodic functions?
That's correct! Fourier integrals allow us to express non-periodic functions as a continuous superposition of sines and cosines. Why is this important?
Because many real-world scenarios, like heat conduction or vibrations, involve non-periodic phenomena.
Exactly! Understanding how to apply Fourier integrals is key in fields like civil engineering.
Application: Heat Diffusion Problem
Unlock Audio Lesson
Let's dive into an engineering problem: heat diffusion in a semi-infinite rod. We're given an initial temperature and an instantaneous heat source. What would our governing equation look like?
It would be the one-dimensional heat equation: ∂u/∂t = α² ∂²u/∂x².
Very good! We apply Fourier transform to convert this PDE into an ODE. Can someone explain why this is beneficial?
It simplifies the problem, making it easier to solve.
That’s right! Once we have the ODE, we can solve for u(ω, t) and take the inverse transform to find our temperature distribution.
Solution Derivation
Unlock Audio Lesson
I want you all to imagine we are solving the equation for u(ω, t) = e^(-α²ω²t). What’s the next step?
We take the inverse Fourier transform of this expression!
Great! Remember, the inverse transform will yield u(x, t). What form does this solution take?
It will be in the form of a Gaussian function, showing how heat diffuses over time.
Precisely! This Gaussian function is what we call the heat kernel. It fundamentally describes transient heat flow.
Significance in Civil Engineering
Unlock Audio Lesson
Finally, why is it crucial for civil engineers to understand Fourier integrals?
To analyze structures under thermal effects and transient conditions.
Yes! These integrals help predict behaviors in real-life scenarios, greatly affecting the designs of structures.
So, does it apply to other areas besides heat diffusion?
Absolutely! It's used in vibration analysis, soil mechanics, and more. Understanding these concepts broadens your engineering toolkit.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section explains how Fourier integrals can express non-periodic functions and solve engineering problems, specifically focusing on heat diffusion in a semi-infinite rod. The governing equations are presented, and the solution method through Fourier transforms is illustrated.
Detailed
Fourier integrals serve as a crucial tool for solving engineering problems involving non-periodic functions. This section begins by presenting an engineering scenario: heat diffusion in a semi-infinite rod subject to an instantaneous heat source. The governing one-dimensional heat equation is introduced, along with its initial and boundary conditions. Through the application of the Fourier transform, the partial differential equation is transformed into an ordinary differential equation, allowing for the extraction of a solution in terms of the Fourier integral. The derived solution highlights the Gaussian function as the heat kernel, showcasing how temperature diffuses through the rod over time. This exemplifies the significance of Fourier integrals in civil engineering and thermal analysis.
Youtube Videos
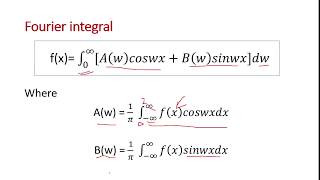
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to the Problem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let’s look at how the Fourier Integral is applied in a real engineering scenario.
Problem: Heat Diffusion in a Semi-Infinite Rod
A rod of infinite length initially at zero temperature receives an instantaneous unit heat source at x=0 at t=0. The governing equation is the one-dimensional heat equation:
∂u/∂t = α² ∂²u/∂x²
With initial condition:
u(x,0) = δ(x)
And boundary condition:
u(±∞,t) = 0
Detailed Explanation
In this section, we are introduced to a practical engineering problem involving heat diffusion. The scenario describes a semi-infinite rod that starts with no temperature and suddenly receives a heat source. The heat diffusion is modeled by the one-dimensional heat equation, which relates how temperature changes over time and space. The equation uses derivatives to describe how the temperature at a point in the rod changes with respect to time and position. The initial condition, which specifies the starting temperature distribution, is represented by δ(x), indicating that all the heat is concentrated at a single point (x=0). The boundary condition states that at large distances from the heat source, the temperature remains zero.
Examples & Analogies
Imagine a long metal rod reaching into the darkness of space—initially at a consistent low temperature. Suddenly, a blowtorch is applied at one point on the rod. Although the blowtorch heats just a small portion, the heat will gradually spread along the entire rod. This represents how heat diffusion works in materials, and we use mathematical equations to predict how quickly and effectively that heat spreads out, which is crucial for designing structures and materials safely.
Transforming the Problem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Taking the Fourier Transform in x, we convert the PDE to an ODE:
∂u(ω,t)/∂t = −α²ω²u(ω,t)
Detailed Explanation
To solve the heat diffusion problem, we apply a mathematical technique known as the Fourier Transform. This transforms the partial differential equation (PDE) that describes temperature changes into an ordinary differential equation (ODE). In simpler terms, this transformation makes the complex heat equation easier to solve by converting it into a format that focuses on a single variable (time), rather than two (time and space). The equation now describes how the temperature at different frequencies (ω) evolves over time, simplifying our analysis.
Examples & Analogies
Think of this transformation as turning a complex recipe into a simplified list of ingredients—a way to break down the original challenge into components that are easier to manage. Instead of juggling multiple tasks at once (like cooking and timing), we can now focus just on how the heat at different parts of the rod behaves over time.
Solving the Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Solving: u(ω,t) = e^{−α²ω²t}
Detailed Explanation
After transforming the problem, we can now solve the ODE for u(ω,t). This solution shows that the temperature response at different frequencies decays exponentially over time. The term e^{−α²ω²t} indicates that higher frequencies dissipate heat more quickly, resulting in a gradual flattening of the temperature profile over time. This solution provides insight into how the temperature at x=0 evolves after the heat source is applied.
Examples & Analogies
Imagine blowing up a balloon. When you first start pumping air (the heat), it quickly expands. But over time, the spray from the nozzle becomes less effective as the balloon gets larger (the heat dissipates). Similarly, the heat created at the source fades over time, and knowing this decay helps engineers predict how materials will react under thermal loads.
Inverse Fourier Transform and Final Results
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Taking the inverse Fourier transform:
1/2π ∫[0,∞] e^{−α²ω²t} e^{iωx} dω
Using the standard Gaussian integral identity:
1/√(4πα²t) e^{−x²/(4α²t)}
This is the heat kernel, a fundamental solution showing how heat diffuses through the rod.
Detailed Explanation
To determine the actual temperature distribution in the physical rod, we apply the inverse Fourier Transform, which reverses our earlier transformation. The resulting formula reflects how temperature at any point x diffuses over time t. The heat kernel—1/√(4πα²t) e^{−x²/(4α²t)}—serves as a fundamental solution to describe this diffusion phenomenon. It shows the relationship between time, the heat source's strength, and how far the heat spreads from the source over time.
Examples & Analogies
Consider a drop of food coloring in a glass of water. Initially, the color is concentrated where it falls, but gradually it spreads out in every direction. The heat kernel provides a mathematical way to predict how that 'color' (heat) disperses through the 'water' (the rod). Knowing this allows engineers to make informed decisions about materials caring for temperature variations, ultimately preventing structural damage.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Fourier Integral: Method for handling non-periodic functions.
-
Heat Diffusion: A concept relevant to engineering physics regarding temperature distribution.
-
Initial and Boundary Conditions: Essential for solving PDEs accurately.
-
Transformation: Converting a PDE into an ODE for simplified analysis.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In civil engineering, the heat diffusion problem can be modeled using Fourier integrals to determine how heat spreads in materials.
-
Similar techniques can be applied to vibration analysis or stress wave propagation in soils.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When heat will flow, it’s slow like a show, through a rod, watch it go as it starts to glow.
📖 Fascinating Stories
-
Imagine a long rod, cold at first. Suddenly, heat flows into it at one end, transforming the rod into a warm glowing beacon over time—this is the heat kernel in action!
🧠 Other Memory Gems
-
For heat diffusion: 'PDE to ODE' - remember to Compute, Transform, and Derive.
🎯 Super Acronyms
F.I.R.S.T - Fourier Integrals Represent Solutions to Transitions in heat diffusion.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fourier Integral
Definition:
A representation of a non-periodic function as a continuous superposition of sine and cosine functions.
-
Term: Heat Kernel
Definition:
A Gaussian function that describes how heat diffuses through a medium over time.
-
Term: PDE
Definition:
Partial Differential Equation, a differential equation involving functions of several variables.
-
Term: ODE
Definition:
Ordinary Differential Equation, a differential equation containing one or more functions of one independent variable.
-
Term: Transform
Definition:
A mathematical operation that converts a function from one domain to another, often simplifying analysis.