Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Structural Vibration Analysis
Unlock Audio Lesson
Today, we will discuss how Parseval's Theorem is applied in structural vibration analysis. Can anyone tell me how this theorem helps engineers calculate energy in vibrating structures?
I think it allows us to understand the energy distribution in both time and frequency domains.
Exactly! By relating the total energy of a structure's response in time to its spectral energy in frequency, engineers can determine the RMS value of vibrations.
So, if we know the Fourier coefficients, we can find out how much energy a structure absorbs during vibrations?
Correct! This ensures that structures can handle dynamic loads without failing. Remember, the more accurately we can compute vibration energies, the better we can design our structures!
What about the accuracy of the Fourier coefficients? Does it matter?
Great question! The Fourier coefficients must represent the actual periodic nature of the loads accurately for reliable results.
In summary, Parseval's Theorem gives engineers a powerful method to compute and understand the energy response of structures subjected to dynamic loads.
Signal Energy in Remote Sensing and Earthquake Data
Unlock Audio Lesson
Next, let’s discuss how seismic signals from structures relate to Parseval’s Theorem. Why is it crucial to analyze these signals in civil engineering?
Because understanding the energy of these signals can help assess how structures respond to earthquakes.
Exactly! By using Parseval's Theorem, engineers can compute the energy of seismic waves directly from their Fourier coefficients. This facilitates effective health monitoring.
Does that mean we could predict how a building behaves during an earthquake?
Yes, precisely! By analyzing the energy computed from seismic data, engineers can determine structural integrity and safety under potential seismic events.
What if the data is not periodic? Can we still use Parseval's Theorem?
That's where the Fourier Transform comes into play! For non-periodic signals, similar principles hold, but in the context of transforms.
So, to wrap up this session, Parseval's Theorem is vital for ensuring the resilience and safety of structures in seismic-prone regions.
Solving Partial Differential Equations
Unlock Audio Lesson
Now, we will learn how Parseval's Theorem is applied in solving partial differential equations. Why do you think it's important in this context?
It could help in calculating energy distributions over space and time in dynamics, right?
Spot on! For example, in heat conduction problems, Parseval's Theorem helps calculate total energy distributed within a system, facilitating understanding of heat transfer.
How does that work specifically?
We utilize Fourier methods to express solutions, and Parseval's identity relates the energies computed over spatial domains directly to those over temporal domains.
So it plays the same role in both the mathematical approach and practical applications?
Exactly! The processes of energy distribution in heat equations are essential in designing effective heat management systems in civil engineering.
Finally, remember that Parseval's Theorem is a cornerstone in understanding energy interactions in both theoretical and practical frameworks.
Modal Analysis in Dynamic Systems
Unlock Audio Lesson
Finally, let's explore how Parseval's Theorem contributes to modal analysis in dynamic systems. Why does this matter in civil engineering?
It helps us understand how different modes contribute to a structure's total response to dynamic loads.
Exactly! In multidegree-of-freedom systems, Parseval's Theorem helps quantify contributions of different vibrational modes to total energy.
Can you give an example of where this is useful?
Certainly! In analyzing bridges or skyscrapers during wind loads, understanding each mode's contribution ensures safety and performance.
What happens if one mode becomes dominant?
If one mode dominates, the structure may experience excessive vibrations, potentially leading to structural failure. Understanding these dynamics is crucial!
In conclusion, Parseval's Theorem is invaluable for engineers to assess response contributions of various modes and design accordingly.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Parseval’s Theorem is pivotal in civil engineering as it allows engineers to analyze periodic loads, vibrations, and stress using harmonic components, thereby facilitating energy calculations in various applications such as structural vibration analysis, remote sensing, and solving partial differential equations.
Detailed
Applications of Parseval’s Theorem in Civil Engineering
Parseval’s Theorem is vital in civil engineering, as it applies the energy equivalence in both time and frequency domains to practical situations in the field. Here are the key applications outlined:
- Structural Vibration Analysis: Civil engineers utilize Parseval's Theorem to analyze how structures like beams and slabs react under periodic loading. The theorem helps compute the energy content or root mean square (RMS) values of vibrational signals derived from their frequency components, facilitating effective responses to dynamic loads.
- Signal Energy in Remote Sensing and Earthquake Data: In structures, seismic signals are often periodic, making Parseval's Theorem instrumental in calculating energies from Fourier coefficients. It assists engineers in monitoring structural health during earthquake events, ensuring safety and stability.
- Solving Partial Differential Equations: In civil engineering problems related to heat conduction and wave equations, Parseval's Theorem allows for the calculation of total energy distribution over time and space, providing insight into how energy evolves in systems governed by differential equations.
- Modal Analysis in Dynamic Systems: In assessing multidegree-of-freedom systems, the theorem aids in interpreting the contributions of different modes of vibration. By analyzing Fourier coefficients that represent modal amplitudes, engineers can determine how each mode contributes to the total system energy during dynamic events.
Overall, Parseval’s Theorem is a transformative tool that enhances structural analysis, enabling engineers to predict responses accurately and maintain system resilience.
Youtube Videos
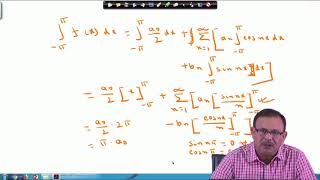
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Structural Vibration Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When a structure like a beam or a slab is subject to periodic loads, the response can be analyzed in terms of its frequency components using Fourier series. Parseval’s Theorem allows engineers to compute the energy content or RMS value of vibration signals from the spectrum.
Detailed Explanation
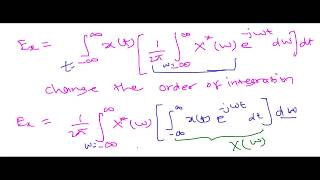
In civil engineering, structures often experience loads that change with time. When these loads are periodic, the response of the structure can be modeled using Fourier series, which breaks the response down into its frequency components. Parseval's Theorem is useful because it connects the energy of the vibration signals in the time domain with the energy in the frequency domain, allowing engineers to determine the root mean square (RMS) value of vibrations and assess the structure's energy content.
Examples & Analogies
Think of a violin string being plucked. The sound it produces can be understood by looking at its different frequency components. Just like analyzing the notes a string produces when plucked, engineers analyze the vibrations of a structure to understand how it responds to loads, ensuring it can withstand forces without failing.
Signal Energy in Remote Sensing and Earthquake Data
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The seismic signals measured from structures or the earth’s surface are periodic in nature. Parseval’s Theorem enables energy calculation directly from Fourier coefficients, which helps in structural health monitoring and earthquake engineering.
Detailed Explanation
Seismic signals collected during earthquakes can be modeled as periodic functions. By applying Parseval's Theorem, engineers can calculate the energy of these signals using the Fourier coefficients derived from the signal's Fourier series representation. This energy calculation is crucial for assessing how much energy a structure can handle during seismic activities, which is vital for structural health monitoring and designing buildings that can withstand earthquakes.
Examples & Analogies
Imagine you are measuring the waves in the ocean. Just as you can calculate the energy of those waves to determine if they're safe for swimming, engineers use Parseval's Theorem to measure the energy of seismic signals to ensure buildings are safe during earthquakes.
Solving Partial Differential Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In problems involving heat conduction (Fourier’s Law) or wave equations in materials, Parseval’s Theorem can be used to compute total heat or energy distributed in the system over time or space.
Detailed Explanation
Many problems in civil engineering involve differential equations that describe physical phenomena like heat conduction or wave propagation. By utilizing Fourier series to express the solutions to these equations, engineers can apply Parseval's Theorem to find the total energy associated with the solution. This approach simplifies the analysis and helps to quantify energy distribution in materials over space and time.
Examples & Analogies
Consider a heated metal rod. Using Fourier series, you could describe the distribution of heat along the rod. Just as you would measure how much heat is distributed at different points to ensure the rod operates safely, engineers use Parseval's Theorem to calculate and manage energy distributions in various materials.
Modal Analysis in Dynamic Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In modal analysis of multi-degree-of-freedom systems (MDOF), the Fourier coefficients represent modal amplitudes. Parseval’s Theorem helps in calculating the contribution of each mode to the total system energy.
Detailed Explanation
In structures with multiple degrees of freedom, such as tall buildings or bridges, each mode of vibration contributes differently to the overall response of the structure. By analyzing these modes using Fourier coefficients, engineers can apply Parseval's Theorem to determine how much energy each individual mode contributes to the system. This information is important for optimizing design and ensuring safety.
Examples & Analogies
Think of a symphony orchestra where different instruments play together, creating a harmonious sound. Each instrument contributes a different part to the overall music, just like each vibrational mode contributes to the overall behavior of a structure. Engineers use Parseval's Theorem to understand the energy contribution from each mode, ensuring they design structures that can handle the combined effects of all the modes.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Energy Equivalence: Parseval's Theorem equates energy in time and frequency domains.
-
Structural Vibration Analysis: Critical in understanding how structures respond to dynamic loads.
-
Fourier Coefficients: Essential for determining energies of signals in both domains.
-
Remote Sensing Applications: Used in evaluating seismic impacts on structures.
-
Modal Analysis: Analyzes how individual vibrational modes contribute to overall structural response.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of calculating the energy content of vibrations in a bridge under train loads using Parseval’s Theorem.
-
Using Parseval’s Theorem to assess structural integrity from seismic data during an earthquake.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Energy in time and frequency flow, Parseval's bridge connects, as structures glow.
📖 Fascinating Stories
-
Imagine an engineer at a bridge site, calculating how vibrations might take flight. With Parseval's theorem by their side, they ensure safety with precision as a guide.
🧠 Other Memory Gems
-
VIBES - Vibration, Important in Bridge Energy Safety.
🎯 Super Acronyms
FEAST - Frequency Energy Analysis in Structural Theorems.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Parseval’s Theorem
Definition:
A principle in Fourier analysis that states the total energy of a signal in the time domain is equal to the total energy in the frequency domain.
-
Term: RMS Value
Definition:
The root mean square value, which is a measure of the magnitude of a varying quantity.
-
Term: Fourier Coefficients
Definition:
Coefficients obtained from the Fourier series representing a periodic function.
-
Term: Structural Vibration
Definition:
Oscillations of structures due to dynamic loads.
-
Term: Modal Analysis
Definition:
The study of a structure’s response to dynamic loads, focusing on the contribution of different vibrational modes.