Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Parseval's Theorem
Unlock Audio Lesson
Welcome class! Today, we will explore Parseval’s Theorem, a fundamental result in Fourier Analysis that connects the energy of signals in both the time and frequency domains. Can anyone tell me why understanding energy is important in engineering?
Is it because we need to analyze how structures respond to different loads?
Exactly! Structural engineers must assess vibrations and stresses caused by various loads. Parseval’s Theorem allows us to link these phenomena through Fourier series. Remember, energy can be observed in both realms!
What does square integrable mean in this context?
Great question! A function is square integrable if the integral of its square is finite over its domain. This condition ensures we can apply Parseval’s Theorem. It’s essential for ensuring that our calculated energy remains relevant.
Mathematical Formulation
Unlock Audio Lesson
Now, let’s look at the mathematical formulation. If we have a periodic function *f(x)* with Fourier coefficients *a_n* and *b_n*, Parseval's identity states: $$ \frac{1}{L} \int_{-L}^{L} |f(x)|^2 dx = a_0^2 + \sum_{n=1}^{\infty} (a_n^2 + b_n^2) $$ Can someone relate this to the concept of energy?
So, on the left side, we have the energy from the time domain, and on the right side, the energy represented in the frequency domain through its coefficients?
Yes, that's correct! This relationship provides engineers a powerful tool to analyze systems more efficiently. If we understand both perspectives, we can design structures that better withstand vibrations.
Applications in Engineering
Unlock Audio Lesson
Now that we understand the theorem mathematically, let’s discuss its applications. One major field is structural vibration analysis. How do you think Parseval’s Theorem applies here?
It could help in calculating how much energy is in a vibration signal from its frequency components.
Exactly! Engineers can compute the energy content of vibrations, allowing them to ensure structures can handle such stresses over time. Can anyone think of another application?
What about signal processing in earthquake data analysis?
Absolutely! Seismic signals are periodic, and Parseval’s Theorem allows engineers to calculate energy directly from those signals, which is crucial for monitoring structural health.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Parseval’s Theorem is a fundamental result in Fourier Analysis, relating the square-integrable norm of a function over its domain to the sum of the squares of its Fourier coefficients. This theorem plays a critical role in fields such as civil engineering, particularly in the analysis of periodic loads and vibrations.
Detailed
Detailed Summary of Parseval’s Theorem
Parseval’s Theorem establishes a powerful relationship between the domain representations of functions and their frequency components. Specifically,
Statement of Parseval’s Theorem: If f(x) is a real, periodic function with a period of 2L and is square integrable over the interval [-L,L], then the total energy (or mean square value) of the function in the time domain, represented as:
$$ \frac{1}{L} \int_{-L}^{L} |f(x)|^2 dx $$
is equivalent to the sum of the squares of its Fourier coefficients, expressed as:
$$ a_0^2 + \sum_{n=1}^{\infty} \left( a_n^2 + b_n^2 \right) $$
Here, a_n and b_n denote the Fourier coefficients derived from the function’s Fourier series expansion. This theorem is instrumental for engineers in a variety of applications ranging from structural dynamics to signal processing. By connecting the time domain to the frequency domain, it allows for the calculation of energies associated with dynamic systems. During practical applications, such as analyzing vibrations or solving differential equations, the theorem ensures that energy calculations are both meaningful and accurate.
Youtube Videos
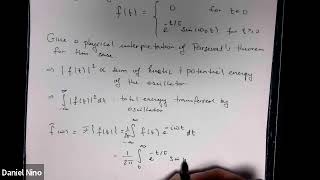
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Parseval’s Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Parseval’s Theorem relates the square-integrable norm (energy) of a function over a period to the sum of the squares of its Fourier coefficients.
Detailed Explanation
Parseval’s Theorem serves to connect the energy a signal has in the time domain to how that same energy can be observed in the frequency domain. Essentially, it states that when you represent a signal as a sum of sinusoids (the Fourier series), the total energy computed in the time domain is equal to the total energy computed from the Fourier coefficients in the frequency domain.
Examples & Analogies
Imagine a musician playing a beautiful melody on a piano. The sound you hear (the time domain) has a certain character and 'energy' based on the notes played. If you were to analyze each individual frequency (the frequency domain), you would find that the total energy represented by those frequencies matches the energy perceived from the melody you heard. Parseval’s Theorem assures you that no energy is lost in translation between these two representations.
Theorem Statement
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Theorem (Parseval’s Identity): If f(x) is a real, periodic function with period 2L, which is square integrable over [−L, L], then:
1 Z L
|f(x)|^2dx = a_0^2 + X_{n=1}^{∞} (a_n^2 + b_n^2)
L 2
−L
Detailed Explanation
The theorem formally states that if we have a function f(x) that is periodic and square integrable, the integral of the square of the function over one full period (from -L to L) is equal to the sum of the squares of its Fourier coefficients. The a_0 term represents the average value of the function over the period, and a_n and b_n are coefficients that describe the amplitude of the cosine and sine components, respectively.
Examples & Analogies
Think of this theorem like an accounting system for energy. If you generate a report of your energy usage over a month (the left side), it should match the tally of each device's usage recorded individually (the right side). Just like those readings, Parseval’s Theorem ensures that the total energy measured in one way equals the total energy measured in another way.
Energy Interpretation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This result means the total mean square value (or energy) of f(x) over the interval is equal to the sum of the squares of its Fourier coefficients.
Detailed Explanation
The essence of Parseval's Theorem provides a deep understanding of energy in dual domains. The total mean square value (energy) of the function f(x) over its interval directly corresponds to the energy captured through its Fourier coefficients. This equivalence is particularly useful for analyzing periodic functions and signals.
Examples & Analogies
Imagine a sports team where players have statistics on their performance (for example, goals scored). Parseval’s Theorem tells us that the overall performance of the team over a season (the overall energy) can be calculated by summing up each player’s performance metrics squared, matching both methods of evaluating success.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Energy: The total mean square value of a function over its interval.
-
Fourier Coefficients: Coefficients obtained in expanding a function in a Fourier series.
-
Orthogonality: A property of sine and cosine functions that allows elimination of cross-terms during integration.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of applying Parseval's theorem on a square wave.
-
Calculating the energy of a triangular waveform using Parseval's theorem.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In Parseval’s domain, energy rules, down to the roots of sine and cosine tools.
📖 Fascinating Stories
-
Imagine a bridge, swaying gently with the wind. Each sway captures energy, in time and frequency it draws, as engineers study, they mustn't ignore, it’s the same energy, just viewed through different doors.
🧠 Other Memory Gems
-
E = F + E (Energy equals sum of Fourier coefficients).
🎯 Super Acronyms
PEE
- Parseval's Energy Equation (to remember the theorem).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Parseval's Theorem
Definition:
A result in Fourier Analysis establishing the equivalence of the total energy of a function in both the time domain and frequency domain.
-
Term: Square Integrable
Definition:
A property of a function whereby the integral of its square over a certain domain is finite.
-
Term: Fourier Series
Definition:
An expansion of a periodic function in terms of an infinite sum of sine and cosine functions.