Parseval’s Theorem
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Energy of Functions
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we'll dive into Parseval’s Theorem, which relates the 'energy' of a signal in the time domain to its frequency domain. Can anyone tell me what we understand by the energy of a function?

I think it's about measuring how much 'power' a signal holds over time.

Exactly! The energy essentially quantifies the signal's 'power' spread over time. In signal processing, this is crucial. Now, how does this relate to Fourier series?

Fourier series help break down a complex function into simpler sine and cosine components, right?

Spot on! Fourier series allows us to analyze signals in a decomposed form, making it easier to work with. Remember this as we move forward.

So, Parseval’s Theorem connects the energy of the original function with its Fourier series?

Exactly! So let’s summarize: energy in the time domain equals the energy calculated from Fourier coefficients in the frequency domain. This principle is foundational in many engineering applications.
Mathematical Formulation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s discuss the mathematical formulation. The statement is that the energy of the function over an interval equals the sum of squares of its Fourier coefficients. Does anyone recall the formula?

It’s something like the integral of the square of the function over the period is equal to the sum of the squares of the coefficients?

"Yes! More specifically,
Applications in Engineering
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s explore some applications of Parseval’s Theorem, particularly in civil engineering and signal analysis. Who can name a field where this theorem is useful?

Maybe in structural dynamics? Analyzing how structures react to different loads?

Exactly! Engineers use this theorem to compute the energy content of vibrations. This is crucial for assessing how structures behave under periodic loads.

And with earthquakes too, right? Parseval’s helps analyze seismic data?

Right again! In earthquake engineering, the seismic signals help us understand the energy distribution, ensuring the structures remain safe and stable.

It seems that Parseval's Theorem has a broad range of applications!

Indeed! It bridges theoretical mathematics with practical engineering problems. Remember this connection as we progress through our coursework.
Working with Examples
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s practice with some examples to solidify our understanding. Who would like to solve for the energy of a square wave using Parseval’s Theorem?

I can try! The square wave is defined on (−π, π)...

Perfect! So, what's the first step?

We need to find the Fourier coefficients first!

Good! And what does Parseval’s Theorem tell us about the energy in relation to those coefficients?

It should equal the integral of |f(x)|² over that interval.

Exactly! Now, let’s calculate it step by step to understand how we apply this theorem concretely.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Parseval's Theorem is a significant concept in Fourier Analysis that highlights the relationship between the energy of periodic functions in time and frequency domains. This theorem is particularly relevant for engineers engaged in structural analysis, as it allows for the assessment of energy content from Fourier coefficients.
Detailed
Detailed Summary
Parseval's Theorem plays a vital role in Fourier Analysis, transforming how engineers and mathematicians assess the energy of functions. It asserts that the total energy of a periodic function over time can be expressed equivalently through the energy present in its Fourier series coefficients, bridging the gap between time domain and frequency domain interpretations.
Key Points Covered:
- Mathematical Preliminaries: Introduced the basic concepts of Fourier series and their coefficients necessary for understanding Parseval's Theorem.
- Statement of Parseval's Theorem: Defined the theorem that connects the square-integrable norm of a function with the sum of the squares of its Fourier coefficients.
- Derivation and Applications: Illustrated the derivation of the theorem and its implications in areas such as structural vibration analysis, remote sensing, and solving PDEs.
- Complex Form and Validity Conditions: Discussed the complex form of the theorem and outlined conditions under which the theorem holds true.
- Applications in Engineering Practices: Explored practical applications in structural engineering and finite element modeling, demonstrating its relevance in the engineering field. The theorem's applications extend to diverse areas, confirming its importance in modern signal processing and structural analysis.
Youtube Videos







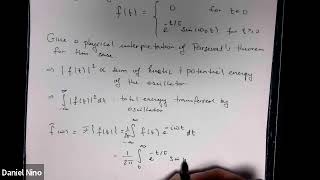


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Parseval’s Theorem
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In engineering mathematics, especially in signal processing and structural analysis, the concept of energy of a function is fundamental. Parseval’s Theorem is a crucial result in Fourier Analysis that equates the total energy of a signal in time domain to its energy in the frequency domain. It provides a powerful bridge between the physical and spectral interpretations of functions and is highly relevant in civil engineering for analyzing periodic loads, vibrations, and stress analysis using harmonic components.
Detailed Explanation
This chunk presents the importance of Parseval’s Theorem in engineering mathematics. It states that the energy of a function, which can be interpreted in both the time domain (how a signal behaves over time) and the frequency domain (how much energy exists at different frequencies), is equal. Understanding this theorem is particularly important for civil engineers who need to analyze structures under various loads and vibrations systematically.
Examples & Analogies
Consider a bridge vibrating when cars pass over it. Each car generates vibrations (time domain) that can be measured as energy. However, engineers also want to know how these vibrations relate to specific frequencies (frequency domain). By applying Parseval's Theorem, they can see that the total energy (or stress response) can be understood as a sum of energies at various frequencies, enabling better design and analysis.
Mathematical Preliminaries
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Before stating and proving Parseval’s Theorem, we review the essentials of Fourier series, as the theorem directly applies to them. Let f(x) be a periodic function defined on [−L,L] and integrable on this interval. Then, the Fourier series of f(x) is given by:
f(x)= a₀ + ∑ (a_n cos(nπx/L) + b_n sin(nπx/L)), where n=1 to ∞.
The Fourier coefficients are defined as:
a₀ = (1/(2L)) ∫[-L,L] f(x)dx,
a_n = (1/L) ∫[-L,L] f(x) cos(nπx/L) dx, (n≥1)
b_n = (1/L) ∫[-L,L] f(x) sin(nπx/L) dx, (n≥1).
Detailed Explanation
This chunk discusses the prerequisites for understanding Parseval’s Theorem, specifically the Fourier series. It defines functions that can be represented as a sum of sine and cosine terms, delineating how these terms capture periodic behaviors. The Fourier coefficients (a₀, a_n, b_n) quantify the contributions of various sine and cosine frequencies within the function. Calculating these coefficients is essential to applying Parseval's Theorem because it connects the time-domain energy to the frequency domain using these coefficients.
Examples & Analogies
Think of a symphony orchestra where different instruments contribute to a single piece of music. Each instrument's notes correspond to parts of the Fourier series. The a₀ coefficient could represent the 'overall volume' of the music, while a_n and b_n would indicate the individual contributions of instruments like the violin and flute to create the complete sound. Understanding these contributions helps in analyzing the harmony or energy of the music as a whole, akin to how Parseval's Theorem relates time and frequency domain energies.
Statement of Parseval’s Theorem
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Parseval’s Theorem relates the square-integrable norm (energy) of a function over a period to the sum of the squares of its Fourier coefficients. Theorem (Parseval’s Identity): If f(x) is a real, periodic function with period 2L, which is square integrable over [−L,L], then:
(1/2L) ∫[-L,L] |f(x)|² dx = (1/(2L)) * (a₀² + ∑ (a_n² + b_n²)), where n=1 to ∞.
Detailed Explanation
This chunk states the formal statement of Parseval’s Theorem. It expresses the idea that the total energy of the function (measured by the integral of the square over its period) is equal to the sum of the squares of the Fourier coefficients. The theorem emphasizes the balance between the total energy representation in the time domain and frequency domain, providing critical insights for engineers analyzing energy distributions.
Examples & Analogies
Imagine measuring the energy consumed in a factory in one day (time domain) versus measuring how much energy each machine uses per hour (frequency domain). Parseval's Theorem tells us that both approaches will give the same total energy consumption. This realization simplifies monitoring and optimizing energy usage, just like how Parseval's Theorem helps engineers analyze energy in structures effectively.
Derivation of Parseval’s Theorem
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
To compute the integral (1/2L) ∫[-L,L] f(x)²dx, we substitute the Fourier series expansion:
(1/2L) ∫[-L,L] f(x)² dx = (1/2L) ∫[-L,L] (a₀ + ∑ (a_n cos(nπx/L) + b_n sin(nπx/L)))² dx.
Using the orthogonality of sine and cosine functions, we find that cross-terms vanish, leading to the conclusion that:
(1/2L) ∫[-L,L] f(x)²dx = (1/2L) (a₀² + ∑ (a_n² + b_n²)), n=1 to ∞.
Detailed Explanation
In this chunk, we explore the steps taken to derive Parseval’s Theorem mathematically. It begins with the integral of the squared function over its period, using the Fourier series representation. By substituting the series and relying on the orthogonality properties of sine and cosine functions (which state that the integral of their product over a full period is zero unless they are the same frequency), we can simplify the expression. This leads us to establish the energy equivalence stated in Parseval’s Theorem.
Examples & Analogies
Picture a musical score where each note represents a different function in our series. When we combine these notes, their combined sound (the integral) should equate to the squared contributions of each note (energy). The orthogonality here ensures that only notes played together matter, akin to how Parseval's Theorem filters out irrelevant sounds in ensuring we accurately capture the total energy from each instrument.
Applications of Parseval’s Theorem in Civil Engineering
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Parseval’s Theorem is particularly useful in the following applications:
1. Structural Vibration Analysis: When a structure like a beam or a slab is subject to periodic loads, the response can be analyzed in terms of its frequency components using Fourier series. Parseval’s Theorem allows engineers to compute the energy content or RMS value of vibration signals from the spectrum.
2. Signal Energy in Remote Sensing or Earthquake Data: The seismic signals measured from structures or the earth’s surface are periodic in nature. Parseval’s Theorem enables energy calculation directly from Fourier coefficients, which helps in structural health monitoring and earthquake engineering.
3. Solving Partial Differential Equations: In problems involving heat conduction (Fourier’s Law) or wave equations in materials, Parseval’s Theorem can be used to compute total heat or energy distributed in the system over time or space.
4. Modal Analysis in Dynamic Systems: In modal analysis of multi-degree-of-freedom systems (MDOF), the Fourier coefficients represent modal amplitudes. Parseval’s Theorem helps in calculating the contribution of each mode to the total system energy.
Detailed Explanation
This chunk outlines practical applications of Parseval’s Theorem in civil engineering. It emphasizes the theorem's versatility in various scenarios, including vibration analysis of structures, energy assessment in seismic data, solving heat conduction problems, and analyzing dynamic systems' behavior. These applications illustrate how Parseval's Theorem aids engineers in predicting the behavior of structures under different conditions and loads.
Examples & Analogies
For example, consider an engineer analyzing vibrations on a bridge due to traffic. By applying Parseval's Theorem, they can determine how much energy the vibrations represent and whether it exceeds safe limits. This is similar to monitoring a busy highway where tracking the total traffic energy can help improve safety protocols based on peak hours and traffic flow.
Key Concepts
-
Energy in Functions: Refers to the power of a function and is a crucial parameter in signal processing and engineering applications.
-
Fourier Series: A method for representing a function as a sum of sine and cosine waves, elucidating the frequency content of the function.
-
Orthogonality: A property of functions that allows simplification in calculations by ensuring certain terms do not interact in the energy calculations.
-
Square-integrable Functions: Functions that are suitable for Fourier analysis and meet certain criteria of finiteness in terms of their squared values.
Examples & Applications
A square wave defined over (-π, π) is used to show how to calculate its energy using Parseval’s Theorem.
A triangular waveform on (-π, π) demonstrate the application of Fourier series coefficients in assessing energy content.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In time and space, the energy flows, Parseval shows where it goes!
Stories
Imagine an engineer assessing a vibrating bridge. They use Parseval's insight to ensure its safety, knowing energy is conserved as it transfers from time domain vibrations to frequency domain waves.
Memory Tools
PEACE: Parseval's Energy And Coefficients Equivalence.
Acronyms
FAME
Fourier
Amplitude
Mean Square Energy.
Flash Cards
Glossary
- Parseval’s Theorem
A theorem that equates the total energy of a function in the time domain to the total energy calculated from its Fourier coefficients in the frequency domain.
- Fourier Series
A series that expresses a function in terms of sinusoids, providing insights into its frequency components.
- Fourier Coefficients
Coefficients obtained from a Fourier series, reflecting the amplitude of respective sine and cosine terms in the series.
- Squareintegrable Function
A function for which the integral of the square of its absolute value is finite, meaning it can be analyzed via Fourier methods.
Reference links
Supplementary resources to enhance your learning experience.
