Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Parseval’s Theorem
Unlock Audio Lesson
Today we're discussing Parseval's Theorem, an essential bridge between time and frequency domains in Fourier Analysis. Can anyone tell me why this theorem is important?
Is it because it helps us understand energy in signals?
Exactly! It equates the total energy of a signal in time domain to its energy in the frequency domain. Can someone explain how we express a function in terms of its Fourier series?
A function gets represented as a sum of sine and cosine terms, plus a constant term.
Great! And these coefficients, $a_n$ and $b_n$, are calculated from integrals. Remember, the orthogonality of these functions is key. Let’s highlight this with a mnemonic; ‘Cosine Meets Sine, Only When It’s Fine!’ This helps remember their interactions.
Deriving the theorem
Unlock Audio Lesson
Now, let's derive Parseval's Theorem. We start by computing the integral of the square of the function. Can anyone help me set up this integral?
We set it up as $\int_{-L}^{L} f(x)^2 dx$?
Exactly! Now, we substitute the Fourier series into the integral. How do we proceed from there?
We expand the square and integrate each term!
Correct! When we integrate, we use the orthogonality property of the sine and cosine functions, leading to the elimination of cross-terms. Can anyone summarize this process?
The orthogonality means that integrals like $\int_{-L}^{L} \cos(nx) \cos(mx) dx$ vanish for $n \neq m$.
Well said! This is the key to our simplified expression and leads to Parseval’s identity. Let's summarize! We derived the theorem by exploiting the orthogonality of trigonometric functions.
Understanding the implications
Unlock Audio Lesson
What implications does Parseval’s Theorem have in engineering, specifically in signal processing?
It helps in analyzing the energy of signals, like vibrations in structures, right?
Yes! It is vital in structural dynamics and computational mechanics. Why do you think knowing energy distribution from Fourier coefficients is beneficial?
It allows engineers to understand how vibrations will affect structures over time.
Exactly! Each mode contributes to the total energy of the system. Let’s remember, ‘Energy Counts in Diverse Frequencies!’ This will help recall how different frequencies affect total energy.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In deriving Parseval's Theorem, we explore the integral of the square of a function expressed as a Fourier series. The section highlights the role of orthogonality of sine and cosine functions and leads to the identity expressing the total energy of a function in terms of the sum of the squares of its Fourier coefficients.
Detailed
Derivation of Parseval’s Theorem
Parseval’s Theorem establishes a critical link between the time domain and frequency domain representations of a periodic function. To derive this theorem, we start with the Fourier series for a real, periodic function
$$ f(x) = a_0 + \sum_{n=1}^{\infty} \left( a_n \cos\left( \frac{n\pi x}{L} \right) + b_n \sin\left( \frac{n\pi x}{L} \right) \right) $$
where the coefficients $a_n$ and $b_n$ are computed from integrals. We then compute the integral of the squared function over one period and substitute the Fourier series into this integral. The orthogonality of the trigonometric functions simplifies the computations greatly, resulting in a neat summation of the squares of the coefficients. This culminates in the identity:
$$ \frac{1}{L} \int_{-L}^{L} |f(x)|^2 dx = \frac{a_0^2}{2} + \sum_{n=1}^{\infty} \frac{a_n^2 + b_n^2}{2} $$
This theorem is significant not only in mathematics but also in civil engineering where it aids in analyzing various structural issues through energy considerations.
Youtube Videos
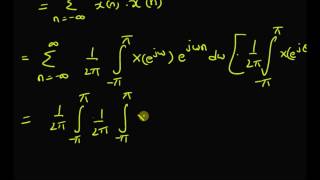
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Fourier Series of a Function
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We start with the Fourier series of f(x):
$$ f(x) = a_0 + \sum_{n=1}^{\infty} \left( a_n \cos \left( \frac{n\pi x}{L} \right) + b_n \sin \left( \frac{n\pi x}{L} \right) \right) $$
Detailed Explanation
In deriving Parseval's Theorem, we begin with the Fourier series representation of a function f(x). This series expresses f(x) as a sum of sine and cosine functions, weighted by coefficients a_n and b_n. The constant term a_0 accounts for the average value of the function over the interval, while the sine and cosine terms capture the oscillatory nature of the function at various frequencies.
Examples & Analogies
Think of the Fourier series as a musical chord, where each sine and cosine function is like an individual note. Just as different notes combine to create harmony in music, these mathematical components work together to reconstruct the original function.
Integral of the Square of f(x)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To compute the integral \( \frac{1}{L} \int_{-L}^{L} f(x)^2 \, dx \), we substitute the Fourier series expansion:
$$ \frac{1}{L} \int_{-L}^{L} f(x)^2 \, dx = \frac{1}{L} \int_{-L}^{L} \left( a_0 + \sum_{n=1}^{\infty} \left( a_n \cos \left( \frac{n\pi x}{L} \right) + b_n \sin \left( \frac{n\pi x}{L} \right) \right) \right)^2 \, dx $$
Detailed Explanation
Next, we need to evaluate the energy of the function f(x) over the interval [-L, L], which is done by computing the integral of its square. We substitute the Fourier series expression for f(x) into this integral. This step sets the stage for examining how the energy represented in the time domain correlates with the coefficients in the frequency domain.
Examples & Analogies
Imagine measuring the total energy of a moving object by tracking its speed over time. The integral of the squared function gives us an aggregate measure of energy, much like how speed multiplied by time gives us distance traveled.
Expanding the Square
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now expanding the square and using the orthogonality of sine and cosine functions:
$$ \int_{-L}^{L} \cos(n\pi x/L) \cos(m\pi x/L) \, dx = \begin{cases} L, & n = m \neq 0 \ 0, & n \neq m \end{cases} $$.
Similarly for sine functions and cross-terms.
Detailed Explanation
Upon expanding the square, we analyze cross-terms involving both sine and cosine functions. The orthogonality property tells us that the integral of the product of two different sine or cosine functions over a complete period yields zero. This means that most mixed terms in the expansion will cancel out, simplifying our calculations.
Examples & Analogies
This is like two musicians playing different instruments. If they play at the same time but in different keys, their sounds blend beautifully, but if they play two different notes, the blend cancels out or becomes silent, which reflects the phenomenon of orthogonality.
Final Simplification
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
After evaluating the integrals and simplifying, all cross terms vanish due to orthogonality, and we are left with:
$$ \frac{1}{L} \int_{-L}^{L} f(x)^2 \, dx = \frac{a_0^2}{2} + \sum_{n=1}^{\infty} \left( \frac{a_n^2 + b_n^2}{2} \right) $$
Detailed Explanation
After simplifying the expression using orthogonality, we arrive at the final form of Parseval's Theorem. This shows that the mean square value (or energy) of the function over the time domain is equal to the sum of the squares of the Fourier coefficients. This relationship indicates that the 'energy' present within the function can be directly computed through its frequency components.
Examples & Analogies
Think of transforming your favorite recipe from cooking (time domain) to a list of ingredients (frequency domain). All the different parts of the recipe contribute to the final dish, just as all frequency components of a function contribute to its overall energy.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Parseval’s Theorem: A theorem that relates the total energy of a signal in time and frequency domains.
-
Energy of a function: The integral of the square of a function, representing its total energy.
-
Fourier Coefficients: Coefficients that express a function in terms of sin and cos functions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If f(x) is a periodic function defined in an interval, Parseval’s Theorem allows calculating the energy over that interval in terms of Fourier coefficients.
-
In a square wave function, by finding Fourier coefficients, we can calculate the total energy easily using Parseval’s identity.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Functions going around, in different domains, energy found!
📖 Fascinating Stories
-
Once there was a wave who loved to dance, shifting between time and frequency, it found its balance. Parseval told its secret, energy's the same, whether in time or frequency, it’s all just a game.
🧠 Other Memory Gems
-
To remember Parseval's identity: 'Every Fourier gives me total energy (E.F.T.E.)'
🎯 Super Acronyms
P.F.E. - Parseval's Fourier Energy helps remember the connection between Parseval and the energy concept.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fourier Series
Definition:
A way to represent a periodic function as a sum of sine and cosine functions.
-
Term: Fourier Coefficients
Definition:
The coefficients derived from a function when expressed in a Fourier series.
-
Term: Orthogonality
Definition:
The property of sine and cosine functions that states they are independent in terms of linear combinations.
-
Term: Energy of a Function
Definition:
The integral of the square of a function over a defined interval, representing its total energy.