Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.

Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.

Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Dominant Pole Calculation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Today, we will explore how to calculate the dominant pole in MOSFET amplifiers. To start off, can anyone tell me why the dominant pole is important?

Is it to understand the bandwidth of the amplifier?

Exactly! The dominant pole affects the -3dB frequency, which determines the frequency response of the amplifier. Now, who knows what the Miller Effect is?

Isn’t it related to C<sub>gd</sub>, the gate-drain capacitance?

Yes! The Miller Effect increases the equivalent capacitance we have to consider, which we will denote as C<sub>eq</sub> and calculate as C<sub>eq</sub> = C<sub>gd</sub>(1 + |A<sub>V</sub>|). This helps us in determining how the capacitance affects our amplifier's frequency response.

So this means the higher the gain, the higher the capacitance?

Correct! And this can limit the bandwidth. We will discuss how to use this to find the -3dB frequency next.

To summarize, the dominant pole calculation is crucial for understanding bandwidth. Remember, C<sub>eq</sub> is affected by the amplifier's gain!
Calculating -3dB Frequency
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Now let’s derive the -3dB frequency. Can anyone tell me what the formula is?

Isn’t it f<sub>-3dB</sub> = 1/(2πR<sub>eq</sub>C<sub>eq</sub>)?

Great! Yes, this formula helps us calculate the frequency at which our amplifier's gain falls to -3dB. What does R<sub>eq</sub> represent in this context?

It's the equivalent resistance seen by the capacitance, right?

Exactly! The value of R<sub>eq</sub> will significantly affect our calculated frequency. Remember, this relationship helps us understand the limitations in our amplifier design.

So if we have a larger resistance, the -3dB frequency gets lower?

Yes! Understanding this relationship is critical for ensuring our amplifier performs as needed within a specified frequency range. To wrap up, the -3dB formula and understanding its components are vital for effective design.
Practical Applications of the Dominant Pole Calculation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson

Now let’s reflect on real-world applications of what we’ve learned. How might this knowledge apply to real MOSFET circuit designs?

It would help in designing amplifiers that need to operate within certain frequency ranges, right?

Correct! Engineers use dominant pole calculations to optimize amplifier performance in circuits, such as in audio applications or RF design. How does this relate to stability?

If we understand how the pole affects bandwidth, we can avoid instability in feedback systems!

Exactly! Balancing gain and bandwidth is key for stability. Doing this helps prevent issues like distortion in audio amplifiers. Remember, good design relies heavily on understanding these principles.

In summary, the dominant pole calculation is not just theoretical but has practical implications that we see in many applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we delve into dominant pole calculation, emphasizing the Miller effect on feedback capacitance (Cgd) and how it impacts the -3dB frequency. Understanding these concepts is crucial for analyzing amplifier performance and determining their frequency characteristics.
Detailed
Dominant Pole Calculation
This section provides essential insights into the dominant pole calculation in MOSFET amplifiers, which plays a significant role in frequency response analysis. We begin with the Miller Effect—an important phenomenon where the feedback capacitance, specifically the gate-drain capacitance (Cgd), effectively increases due to the voltage gain of the amplifier. We calculate the equivalent capacitance (
Ceq) as follows:
$$
C_{eq} = C_{gd}(1 + |A_V|)
$$
Here, AV is the voltage gain of the amplifier, indicating how changes in the input signal affect the output. The dominant pole of the amplifier can be characterized by its -3dB frequency, which is calculated using the following formula:
$$
f_{-3dB} = \frac{1}{2\pi R_{eq}C_{eq}}
$$
Req represents the equivalent resistance seen by the capacitive load and plays a crucial role in determining the bandwidth and stability of the amplifier. Understanding these parameters is vital for designing effective MOSFET amplifier circuits, as they directly influence performance metrics like gain and bandwidth.
Youtube Videos

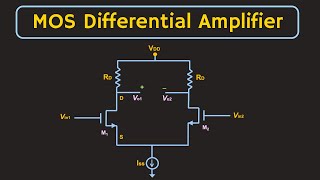
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Miller Effect on C<sub>gd</sub>
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The effective capacitance due to the Miller effect is calculated as:
\[
C_{eq} = C_{gd}(1 + |A_V|)
\]
Detailed Explanation
The Miller effect is an important phenomenon in electronics, particularly in amplifiers. It describes how a capacitance (in this case, Cgd, also known as gate-drain capacitance) appears larger due to the amplification factor of the circuit (AV). The equation indicates that the effective capacitance (Ceq) increases with the magnitude of voltage gain (|AV|). This increase in capacitance can affect the frequency response and stability of the amplifier.
Examples & Analogies
Think of the Miller effect as a water hose. If you keep the hose's diameter fixed (this is like the capacitance), and you increase the pressure of the water (this is like increasing the voltage gain), the flow rate appears to increase significantly. So, in audio applications, if you amplify a weak signal too much, the resulting effect can cause distortions, much like too much water pressure can burst the hose.
-3dB Frequency Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The -3dB frequency, which indicates the cutoff frequency of the amplifier's response, is computed using:
\[
f_{-3dB} = \frac{1}{2\pi R_{eq} C_{eq}}
\]
Detailed Explanation
The -3dB frequency, denoted as f-3dB, is a critical parameter in determining how an amplifier behaves at different frequencies. It tells us the frequency at which the output power drops to half its maximum value, corresponding to a reduction of 3 decibels in voltage gain. The equation shows that this frequency depends on both the equivalent resistance (Req) and capacitance (Ceq) of the circuit. A higher Req or a lower Ceq will result in a higher -3dB frequency, allowing the amplifier to operate at higher frequencies.
Examples & Analogies
Imagine you're tuning a radio. The -3dB frequency is like the point where the music transitions from clear and full to muffled and hard to hear. If the radio’s components allow low resistance (low Req), and the capacitors are efficiently chosen (low Ceq), then better sound quality, or frequency response, is achieved. Think of Req as the clarity of the signal and Ceq as the filter that ensures no annoying static.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Dominant Pole: The primary pole affecting amplifier frequency response.
-
Miller Effect: An increase in effective capacitance due to voltage gain.
-
Equivalent Capacitance (Ceq): Total capacitance considering the Miller Effect.
-
-3dB Frequency: The frequency at which output power is halved, crucial for bandwidth.
-
Equivalent Resistance (Req): Resistance seen by capacitance for -3dB frequency calculation.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If a MOSFET amplifier has a voltage gain of -10 and Cgd = 10 pF, the equivalent capacitance, Ceq, would be 100 pF before calculating the -3dB frequency.
-
Using Req = 1 kΩ and Ceq = 100 pF in the -3dB formula, f-3dB is calculated as 1.59 kHz.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To find Ceq, just take Cgd, add one to AV's head, plug them in, watch it spread; Miller's effect is what we said.
📖 Fascinating Stories
-
Imagine an amplifier on a stage, gaining applause (voltage), but as the crowd (gain) grows, so does the echo (Cgd), affecting sound (frequency) clarity.
🧠 Other Memory Gems
-
Ceq = Cgd (1 + |AV|) can be remembered as 'Capacitance Grows with Amplifier Values'.
🎯 Super Acronyms
C<sub>eq</sub>, R<sub>eq</sub>, f<sub>-3dB</sub>
- Remember CRF! (Capacitance
- Resistance
- Frequency - the key elements in dominant pole calculations.)
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Dominant Pole
Definition:
The pole of a transfer function that has the largest impact on frequency response.
-
Term: Miller Effect
Definition:
A phenomenon where the effect of feedback capacitance increases due to gain, impacting frequency response.
-
Term: Equivalent Capacitance (C<sub>eq</sub>)
Definition:
The total capacitance that includes effects from feedback capacitance, adjusted by voltage gain.
-
Term: 3dB Frequency
Definition:
The frequency at which the output power drops to half its maximum value.
-
Term: Equivalent Resistance (R<sub>eq</sub>)
Definition:
The resistance seen by the equivalent capacitance in the calculation of the -3dB frequency.

