Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Dominant Pole Calculation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we'll dive into the concept of the dominant pole in MOSFET amplifiers. Can anyone tell me what a pole is in this context?
Isn't it where the gain starts to drop significantly?
Exactly! It's a critical point where the transfer function changes. In our case, the dominant pole is significantly influenced by the Miller Effect, particularly through C<sub>gd</sub>. So, if we have a negative voltage gain, how do we express the equivalent capacitance?
I think itβs C<sub>eq</sub> equals C<sub>gd</sub> times one plus the absolute value of A<sub>V</sub>?
Correct! So, when calculating the -3dB frequency, we use f<sub>-3dB</sub> = 1/(2ΟR<sub>eq</sub>C<sub>eq</sub>). Why is this frequency significant?
It indicates where the amplifier's output drops to 70.7% of the maximum!
Very good! Remember this fact; itβs a vital part of our analysis.
Gain-Bandwidth Product (GBW)
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's switch gears to the Gain-Bandwidth Product, or GBW. Has anyone encountered this term before?
I have! Isnβt it a measure of how bandwidth decreases as gain increases?
Exactly! It's given by the equation GBW = |A<sub>V0</sub>| Γ f<sub>-3dB</sub>. Who can tell me why this is important?
I think it helps in designing amplifiers to ensure they meet specific performance criteria!
Spot on! The GBW allows us to predict the behavior of our amplifiers across different frequencies while maintaining desired gain levels.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The frequency response of MOSFET amplifiers is critical for understanding their performance. This section introduces the concept of the dominant pole and how the Miller Effect affects capacitance, as well as how Gain-Bandwidth Product (GBW) is defined and calculated.
Detailed
In this section on Frequency Response, we explore significant concepts essential for analyzing MOSFET amplifiers' performance in varying frequencies. The dominant pole calculation considers the Miller Effect, highlighting how the capacitance is influenced by voltage gain, outlined as Ceq = Cgd(1 + |AV|). We also derive the -3dB frequency of the amplifier, given by f-3dB = 1/(2ΟReqCeq), where Req represents the equivalent resistance. Understanding these factors culminates in the Gain-Bandwidth Product (GBW), an important metric calculated by the formula GBW = |AV0| Γ f-3dB. Analyzing these aspects provides insight into application efficiency and performance of amplifiers in various operational settings.
Youtube Videos
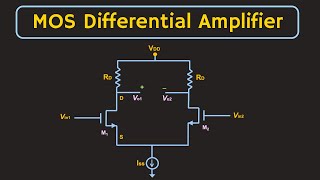
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Dominant Pole Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
5.6.1 Dominant Pole Calculation
- Miller Effect on Cgd:
\[ C_{eq} = C_{gd}(1 + |A_V|) \] - -3dB Frequency:
\[ f_{-3dB} = \frac{1}{2ΟR_{eq}C_{eq}} \]
Detailed Explanation
The Dominant Pole Calculation section primarily focuses on how the frequency response of an amplifier can be determined. The Miller Effect refers to an increase in capacitance seen by the amplifier, which is influenced by the gain (AV). Specifically, the equivalent capacitance (Ce) is found by multiplying the gate-drain capacitance (Cgd) with the factor (1 + |AV|). This means that as the amplifier gain increases, the effective capacitance seen by the input also increases. Subsequently, the -3dB frequency is calculated using the equivalent resistance and capacitance, which indicates the point at which the output power drops to half its maximum value. This frequency is crucial because it marks the bandwidth limit of the amplifier: frequencies beyond this point will have significantly lower gain.
Examples & Analogies
Think of a water pipe system where the pressure (analogous to gain) in a section of the pipe causes a back pressure at the entry point. The effect of this back pressure can be compared to the Miller Effect, which makes the pipe appear larger (higher capacitance). Just like too much pressure can burst a pipe, exceeding the -3dB frequency can lead to inadequate performance of an amplifier, impacting the design just like a failing plumbing system can disrupt water flow in a house.
Gain-Bandwidth Product
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
5.6.2 Gain-Bandwidth Product (GBW)
\[ GBW = |A_{V0}| Γ f_{-3dB} \]
Detailed Explanation
The Gain-Bandwidth Product (GBW) is a critical concept in understanding amplifier performance. It articulates the relationship between an amplifier's gain (AV0) at low frequencies and its bandwidth (the range of frequencies over which an amplifier can effectively operate). Essentially, if you multiply the voltage gain at a specific frequency by the bandwidth, you get a constant value known as the GBW. This is important because it implies that as you increase the gain of an amplifier, its bandwidth decreases, and vice versa. Designers must consider this trade-off when designing circuits to meet specific performance criteria.
Examples & Analogies
Imagine a music band playing at an event. If the band plays at a lower volume (similar to lower gain), they can reach a larger audience (wider bandwidth). However, if they turn up the volume (higher gain), they can only fill a smaller venue without causing distortion. The GBW acts like a commitment they make to balance their performance; the louder they play, the less people can enjoy the concert outdoors.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Dominant Pole: The frequency point where the gain of an amplifier significantly decreases.
-
Miller Effect: Increases the effective input capacitance in amplifiers.
-
Gain-Bandwidth Product (GBW): Metric indicating the relationship between the gain and bandwidth of an amplifier.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of calculating the -3dB frequency for a given amplifier configuration using the derived formula.
-
Calculating the Gain-Bandwidth Product for a hypothetical MOSFET amplifier with an initial gain of 10 and a -3dB frequency of 2 MHz.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
To find pole light, take the gain's might; Miller's role makes capacitance quite.
π Fascinating Stories
-
Imagine an amplifier at a party, where the loudness is like the gain, and when too many guests (input signals) arrive, the music fades (frequency drops). The point where it fades to just enough to keep dancing is the -3dB frequency, a sweet spot that must be managed.
π§ Other Memory Gems
-
G-B-P: Gain-Bandwidth Product is like a balanced scaleβmore gain means less bandwidth.
π― Super Acronyms
MGB for Miller's Gain Bandwidth
- M: for Miller Effect
- G: for Gain
- B: for Bandwidth.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Miller Effect
Definition:
A phenomenon in amplifiers where the effective capacitance increases due to the interaction between the input and output voltages.
-
Term: 3dB Frequency
Definition:
The frequency at which the output power of a system is half of the maximum output power.
-
Term: GainBandwidth Product (GBW)
Definition:
A constant value for a given amplifier that indicates the trade-off between gain and bandwidth.