Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Ideal Gas Equation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, weβre going to explore the ideal gas equation: PV = Β΅RT. Can anyone tell me what each of those letters represents?
P is pressure, V is volume, Β΅ is moles, R is the universal gas constant, and T is temperature!
Exactly right! This equation shows how pressure, volume, and temperature are related for an ideal gas. Letβs start with pressure. Why do you think pressure increases when volume decreases?
Because if the space for the gas decreases, the molecules collide more often with the walls, increasing pressure!
Perfect! This is a concept known as Boyleβs Law.
Understanding Absolute Zero
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs discuss absolute zero, which is 0 K or -273.15 Β°C. Can anyone tell me what absolute zero signifies?
Itβs the temperature at which molecular motion stops completely!
That's right! It's the foundation of the Kelvin scale. Why do we need this absolute scale?
Because it gives us a consistent way to measure temperature, especially in scientific equations!
Exactly! And having both Celsius and Kelvin scales helps us convert temperatures easily. Remember, T(K) = t(Β°C) + 273.15.
Charles's Law and Boyle's Law
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs apply our knowledge now with Boyle's and Charlesβ Laws, starting with Boyle's Law. What happens to a gas when we decrease its volume while keeping temperature constant?
The pressure increases!
Good! And what about Charles' Law, which concerns volume and temperature?
If we increase the temperature, the volume increases if pressure is constant!
Exactly! So these relationships form the basis of why the ideal gas law works.
Real Gases vs Ideal Gases
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
While we base many calculations on ideal gases, real gases can deviate from this model. Who can think of conditions where this occurs?
At high pressures and low temperatures, right?
Yes! Under those conditions, interactions between gas molecules become significant, altering their behavior from the ideal model. Always remember these deviations!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The ideal gas equation links pressure, volume, temperature, and the number of moles of a gas, leading to the understanding of absolute temperature. This concept is essential in physics as it helps describe the behavior of gases under various conditions and is foundational for thermodynamics.
Detailed
Detailed Summary
The ideal gas equation, expressed as PV = Β΅RT, relates the pressure (P), volume (V), temperature (T), and the amount of substance (Β΅) in moles of an ideal gas. In this equation, R represents the universal gas constant (8.31 J molβ1 Kβ1). Here, T is the absolute temperature measured in Kelvin.
Absolute Temperature:
The absolute temperature scale begins at absolute zero (0 K), which corresponds to -273.15 Β°C. This temperature is critical because it signifies the point where molecular motion ceases. The relationship between Kelvin and Celsius temperature scales can be expressed as T = tΒ°C + 273.15. It is important to understand that all finite gas volumes tend to zero at absolute zero temperature.
The section also discusses how the ideal gas behaves under different conditions, such as Boyle's Law (constant temperature) and Charles's Law (constant pressure). These relationships allow for simplifying calculations and understanding gas behavior considerably.
Finally, the discussions include insights about how real gases can differ from ideal gases under specific conditions, particularly at high pressures or low temperatures.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Gas Thermometer Readings
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Liquid-in-glass thermometers show different readings for temperatures other than the fixed points because of differing expansion properties. A thermometer that uses a gas, however, gives the same readings regardless of which gas is used.
Detailed Explanation
This chunk explains that traditional liquid-in-glass thermometers can give varying readings based on the liquid's expansion properties, while gas thermometers provide consistent readings across different gases. The consistency means that gas thermometers are more reliable for measuring temperature.
Examples & Analogies
Imagine using different types of fluids in a thermometer, like water and mercury. Each fluid expands differently when heated, which can lead to incorrect temperature readings. But if you use gas, like a helium-filled thermometer, it consistently provides the same reading regardless of the gas type, similar to how a well-calibrated shop scale gives accurate weights no matter the item you're weighing.
Behavior of Gases
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Experiments show that all gases at low densities exhibit the same expansion behavior. The variables that describe the behavior of a given quantity (mass) of gas are pressure, volume, and temperature (P, V, and T) (where T = t + 273.15; t is the temperature in Β°C).
Detailed Explanation
This chunk introduces the concept that gases behave predictably under low density conditions, which is important for understanding gas laws. It emphasizes the relationship between pressure, volume, and temperature, and the conversion to Kelvin by adding 273.15 to Celsius.
Examples & Analogies
Think about how a balloon behaves when you heat it. The gas inside expands (volume increases) when heated, and if the balloon is sealed, the pressure inside increases. This is a practical demonstration of how temperature, volume, and pressure relate to one another in gases, akin to holding a soda can with gas inside; shaking it (increasing pressure) causes it to fizz when opened (release of gas).
Boyleβs and Charlesβ Laws
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When temperature is held constant, the pressure and volume of a quantity of gas are related as PV = constant. This relationship is known as Boyleβs law. When the pressure is held constant, the volume of a quantity of gas is related to the temperature as V/T = constant. This relationship is known as Charlesβ law.
Detailed Explanation
Boyleβs law states that if the temperature of a gas remains constant, compressing the gas (decreasing volume) increases the pressure. Conversely, Charlesβ law states that at constant pressure, increasing the gas's temperature results in an increase in its volume. This highlights how gases expand or contract based on temperature and pressure.
Examples & Analogies
Consider a bike pump. When you push down on the pump handle (reducing volume), the air pressure inside increases, making it harder to push down further β this relates to Boyle's law. Now think of a hot air balloon; as the air inside heats up, it expands and fills the balloon with more volume, allowing it to rise. This is an illustration of Charles' law in action.
Ideal Gas Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Low-density gases obey these laws, which may be combined into a single relationship. Notice that since PV = constant and V/T = constant for a given quantity of gas, then PV/T should also be a constant. This relationship is known as the ideal gas law, or PV = Β΅RT, where Β΅ is the number of moles in the sample of gas and R is called universal gas constant.
Detailed Explanation
The ideal gas law combines Boyle's and Charles' laws into a single equation, enabling predictions about gas behavior under varying conditions of pressure, volume, and temperature. The universal gas constant (R) facilitates calculations involving different gases by relating the number of moles to the gas's behavior.
Examples & Analogies
Consider a sealed container of a gas. If you heat the gas, it expands (increases volume). According to the ideal gas law, you can calculate how much the pressure will increase if you know the initial conditions. This principle underpins applications like understanding how car tires inflate when driven on hot days.
Concept of Absolute Zero
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
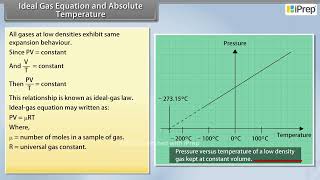
However, measurements on real gases deviate from the values predicted by the ideal gas law at low temperature. But the relationship is linear over a large temperature range, and it looks as though the pressure might reach zero with decreasing temperature if the gas continued to be a gas. The absolute minimum temperature for an ideal gas, therefore, inferred by extrapolating the straight line to the axis, is -273.15 Β°C and is designated as absolute zero.
Detailed Explanation
Absolute zero is defined as the temperature at which the molecular motion of a gas theoretically stops. The chunk discusses that at very low temperatures, real gases do not behave ideally, and the extrapolation of gas behavior suggests this minimum temperatureβ-273.15 Β°C or 0 K.
Examples & Analogies
Visualize a graph plotting temperature against pressure for different gases. As the temperature approaches absolute zero, the line drops, suggesting the pressure becomes zero. This is similar to stopping the movement of a spinning top until it eventually stops completely, indicating that particles canβt move at absolute zero.
Absolute Temperature Scale
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Absolute zero is the foundation of the Kelvin temperature scale or absolute scale temperature named after the British scientist Lord Kelvin. On this scale, -273.15 Β°C is taken as the zero point, that is 0 K. The size of unit in Kelvin and Celsius temperature scales is the same.
Detailed Explanation
This chunk explains how Lord Kelvin established the Kelvin temperature scale based on the concept of absolute zero. It clarifies that while both the Kelvin and Celsius scales are related, Kelvin starts from absolute zero, allowing for absolute temperature measurements in scientific data.
Examples & Analogies
Just like how zero on a thermometer indicates freezing water in Celsius, 0 K represents a complete stop of molecular movement. Think of Kelvin as a more universal scale for scientists when measuring extremely cold gases and ensuring equations do not produce negative temperatures, which can be non-physical in certain contexts.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Ideal Gas Equation: Relates pressure, volume, temperature and number of moles of an ideal gas.
-
Absolute Zero: The temperature at which molecular motion ceases, marking 0 K.
-
Boyle's Law: Describes the inverse relationship between pressure and volume at constant temperature.
-
Charles's Law: Describes the direct relationship between volume and temperature at constant pressure.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using the ideal gas equation PV = Β΅RT, calculate the pressure of a gas if the volume is 2 mΒ³, temperature is 300 K, and amount is 0.5 moles.
-
Explain how a balloon expands as it warms up based on Charlesβ Law.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
When pressure's high, the volume's low, gas behavior is what we all should know.
π Fascinating Stories
-
Once a gas was captured in a perfect balloon, warm it up to see it bloom. As the heat would rise, so would its size!
π§ Other Memory Gems
-
Remember 'PV = nRT' for ideal gases' destiny!
π― Super Acronyms
GAS = 'G' for gas constant, 'A' for absolute temperature, 'S' for state equations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Ideal Gas Equation
Definition:
The equation that relates the pressure, volume, amount of substance, and temperature of an ideal gas, expressed as PV = Β΅RT.
-
Term: Absolute Zero
Definition:
The theoretical temperature at which a system's entropy reaches its minimum, corresponding to 0 K or -273.15 Β°C.
-
Term: Boyle's Law
Definition:
A principle stating that the pressure of a gas is inversely related to its volume when temperature is held constant.
-
Term: Charles's Law
Definition:
A principle stating that the volume of a gas is directly proportional to its temperature when pressure is held constant.