CELLS EMF INTERNAL RESISTANCE
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Electromotive Force (emf)
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will discuss electromotive force, or emf. Can anyone tell me what emf represents in an electrolytic cell?

Isn't it the voltage difference between the two electrodes?

Exactly! It’s important to note that while the emf is a voltage, it is not a force. The formula for calculating emf is `e = V_+ + V_-`, where `V_+` and `V_-` are the potentials of the positive and negative electrodes, respectively.

So, if there’s no current, this is the maximum potential across the terminals, right?

Right again! This is the open-circuit potential. You can think of it as the 'maximum' push of the cell when no current flows.
Impact of Internal Resistance
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

What happens when we connect a load resistor to our cell?

The current starts flowing through the circuit.

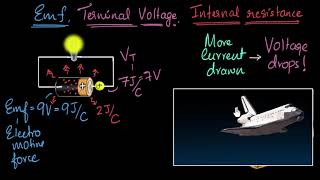
That's right! But there's also a drop in voltage across the load due to internal resistance, which we can model with the equation `V = e - I r`. Can anyone explain this equation?

It shows that the terminal voltage is less than the emf because of the internal resistance `r` multiplied by the current `I`.

Exactly! This internal resistance is crucial when ensuring our circuit functions properly.
Calculating Maximum Current
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

We've discussed how internal resistance affects terminal voltage. Now, let’s consider the maximum current available from a cell. What is the formula for that?

I think it's `I_{max} = e / r`. Right?

Correct! The maximum current occurs when the external load resistance is zero. This is helpful in practical applications to avoid damaging the battery.

So, if we know the emf and internal resistance, we can plan our circuit better?

Exactly! Knowing these values helps us design circuits that avoid excessive current draw.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section delves into how an electrolytic cell generates an electromotive force (emf) and the role of internal resistance in determining the usable voltage across an external load. It highlights the potential difference at the electrodes and the impact of current flow on the voltage, providing equations to quantify these relationships.
Detailed
Cells EMF Internal Resistance
In this section, we explore electrolytic cells, which maintain a steady current in circuits and consist of two electrodes immersed in an electrolyte. The electromotive force (emf) of the cell, denoted as e, is defined as the potential difference between the positive and negative electrodes when no current flows through the circuit. For a simple model, the emf can be expressed as:
$$
e = V_+ + V_-
$$
where V_+ is the potential difference of the positive terminal relative to the electrolyte, and V_- is the potential difference of the negative terminal.
When a resistor R is connected across the cell, the current I flows in the circuit, leading to a drop in terminal voltage due to internal resistance r that exists in the electrolyte. This is represented by the equation:
$$
V = e - I r
$$
The significance of this relationship lies in understanding the limitations imposed by internal resistance, which impacts the effective voltage available for work in the circuit. Additionally, the maximum current that the cell can deliver occurs when the resistance is zero, thus revealing the relationship of maximum current derived from:
$$
I_{max} = \frac{e}{r}
$$
This section emphasizes the importance of considering internal resistance in the design and analysis of circuits that involve electrolytic cells.
Youtube Videos








Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Cells and Emf
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
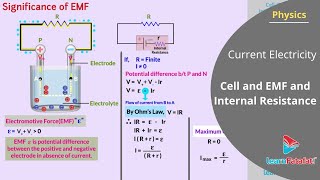
We have already mentioned that a simple device to maintain a steady current in an electric circuit is the electrolytic cell. Basically a cell has two electrodes, called the positive (P) and the negative (N), as shown in Fig. 3.12. They are immersed in an electrolytic solution. Dipped in the solution, the electrodes exchange charges with the electrolyte. The positive electrode has a potential difference V (V > 0) between itself and the electrolyte solution immediately adjacent to it marked A in the figure. Similarly, the negative electrode develops a negative potential –(V )(V ≥ 0) relative to the electrolyte adjacent to it, marked as B in the figure. When there is no current, the electrolyte has the same potential throughout, so that the potential difference between P and N is V – (–V ) = V + V . This difference is called the electromotive force (emf) of the cell and is denoted by e. Thus e = V + V > 0. Note that e is, actually, a potential difference and not a force. The name emf, however, is used because of historical reasons, and was given at a time when the phenomenon was not understood properly.
Detailed Explanation
In this section, we are discussing the concept of an electrolytic cell, which is used to maintain a steady current in an electric circuit. An electrolytic cell consists of two electrodes: the positive (P) and negative (N). The electrodes are immersed in an electrolyte, which allows them to exchange charges. The positive electrode has a higher potential compared to the surrounding solution adjacent to it (point A), while the negative electrode has a lower potential (point B). When there is no current, the potential throughout the electrolyte remains constant, and the total potential difference between the two electrodes is quantified as the electromotive force (emf) of the cell, denoted by e. This emf is simply a measure of the potential difference and is critical for understanding how current flows in the circuit.
Examples & Analogies
Think of an electrolytic cell like a water tank system. The positive electrode is like a water inlet at a higher elevation, while the negative electrode is a drain at a lower elevation. The difference in height (potential difference) between these two points determines how easily water (current) can flow through the system. Just as water flows from high to low elevation, electric charges flow from the positive electrode to the negative one in a circuit.
The Role of Resistance in Current Flow
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
To understand the significance of e, consider a resistor R connected across the cell (Fig. 3.12). A current I flows across R from C to D. As explained before, a steady current is maintained because current flows from N to P through the electrolyte. Clearly, across the electrolyte the same current flows but from N to P, whereas through R, it flows from P to N. The electrolyte through which a current flows has a finite resistance r, called the internal resistance. Consider first the situation when R is infinite so that I = V / R = 0, where V is the potential difference between P and N. Now, V = Potential difference between P and A + Potential difference between A and B + Potential difference between B and N = e.
Detailed Explanation
This chunk explains what happens when a resistor is connected across the electrolytic cell. We denote the fixed resistor as R and consider how a current I flows through it. The internal resistance of the electrolyte is denoted as r. If R is infinite, no current flows through it, meaning the current would be zero. The potential difference across terminals will only be determined by the electromotive force (emf) of the cell, denoting that current will only flow under the emf's influence. This emphasizes the importance of considering internal resistance when analyzing real working circuits.
Examples & Analogies
Imagine a garden hose with a nozzle (the resistor) attached. If you block the nozzle (making R infinite), no water (current) flows through the hose. However, if you allow the hose to be open (having a resistor with low resistance), water flows freely. The internal resistance of the hose (like r) must be accounted for because it dictates how much water can actually flow through the nozzle when it is open.
Calculating Current Flow with Emf and Resistance
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If however R is finite, I is not zero. In that case the potential difference between P and N is V = V + V – I r = e – I r. Note the negative sign in the expression (Ir) for the potential difference between A and B. This is because the current I flows from B to A in the electrolyte. In practical calculations, internal resistances of cells in the circuit may be neglected when the current I is such that e >> I r. The actual values of the internal resistances of cells vary from cell to cell. The internal resistance of dry cells, however, is much higher than the common electrolytic cells.
Detailed Explanation
This part illustrates what happens when a resistor R has a finite value, meaning that current I is now flowing. The potential difference between the electrodes is expressed in the equation V = e – Ir. Here, e is the electromotive force and Ir denotes the voltage drop due to internal resistance. The negative sign indicates that the internal resistance opposes the flow of current. In practical scenarios, if the emf is significantly larger than the drop across internal resistance, the internal resistance can often be ignored for simpler calculations.
Examples & Analogies
Think about riding a bicycle uphill (the emf) and feeling the wind resistance (the internal resistance). When you're pedaling hard (current), you can still make progress, but the wind slows you down (the internal resistance). If you pedal much harder (when e is significantly larger), the effect of the wind becomes less significant in your overall speed.
Maximum Current from a Cell
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We also observe that since V is the potential difference across R, we have from Ohm’s law V = IR. Combining Eqs. (3.38) and (3.39), we get I R = e – I r. Or, I= e / (R + r). The maximum current that can be drawn from a cell is for R = 0 and it is I_max = e/r. However, in most cells the maximum allowed current is much lower than this to prevent permanent damage to the cell.
Detailed Explanation
Here, we derive the equation for calculating the current (I) that can be obtained from an electrolyte cell, taking internal resistance into account. When we use Ohm's law (V = IR), we combine the equations to express the maximum current possible from a cell. The maximum current occurs when R equals zero because all the voltage contributes to driving current through internal resistance r. However, in practice, cells are designed to prevent this maximum flow to avoid damaging themselves.
Examples & Analogies
Picture a water tap (the resistor) attached to a water tank (the cell). When the tap is closed (R = 0), water pressure (the maximum current) in the tank can reach its peak. But if you open the tap too wide, you risk breaking the fixture (cell damage). Manufacturers set limits so you can only partially open it to prevent any overflow or breakage.
Key Concepts
-
Electromotive Force (emf): The voltage created by an electrolytic cell when no current flows.
-
Internal Resistance: Resistance within a cell that impacts the voltage during current flow.
-
Terminal Voltage: The voltage available at the battery terminals when a load is connected.
-
Load Resistor: The external resistance added to the circuit impacting performance.
Examples & Applications
An example of two different electrolytic cells showing varying emf due to internal resistance.
Calculation of terminal voltage across a load resistor when a specific current is drawn from a cell.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
EMF gives the voltage we see, Internal Resistance brings it down, oh me!
Stories
Picture a river (current) flowing, the banks (internal resistance) constrict the flow, affecting the speed as it goes.
Memory Tools
E = V - I*r. Remember: EMF equals the total voltage minus the drop!
Acronyms
R.I.P (Resistance Impacts Power)
Remember
internal resistance impacts power delivery.
Flash Cards
Glossary
- Electromotive Force (emf)
The potential difference produced by a cell when no current flows.
- Internal Resistance
The resistance within the cell that causes a voltage drop when current flows.
- Terminal Voltage
The voltage available across the terminals of a battery when current is drawn.
- Load Resistor
An external resistor connected to a battery or cell in a circuit.
Reference links
Supplementary resources to enhance your learning experience.
