Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Ohm's Law
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to explore Ohm's Law, which establishes the relationship between voltage, current, and resistance. Can anyone tell me what happens to the current if we increase the voltage across a conductor?
I think the current would increase if the voltage increases.
Exactly! This relationship is mathematically expressed as V = RI, where V is the voltage, I is the current, and R is the resistance. We can say that 'voltage is like the pressure pushing the water through a pipe' so if we increase the pressure, more water flows.
So, if I understand correctly, resistance is like the size of the pipe? A larger pipe allows more water to flow?
Spot on! Resistance works the same wayβhigher resistance means less current will flow for a given voltage. Remember the saying, 'R for resistance, Rs for restricts current!'
What units do we use for resistance?
Great question! The unit of resistance is the Ohm, represented by the symbol Ξ©. At the end of this discussion, you'll find it beneficial to remember: 'Ohmβs Law ties V, I, and R together in a single equation!' Let's dive deeper into how resistance depends on the material properties.
Dependence of Resistance
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs discuss how resistance varies not only by the voltage applied but also by the dimensions of the conductor. Who can summarize how changing the length or area affects resistance?
If we increase the length, resistance goes up, but if we increase the area, resistance goes down, right?
Absolutely! The relationship can be remembered with the phrase 'longer means stronger resistance, wider means weaker resistance.' We can express this with equations to show R β l (length) and R β 1/A (area).
What does resistivity have to do with that?
Excellent question! Resistivity is a material property that quantifies how strongly a material opposes the flow of electric current. The formula R = Ο(l/A) articulates that resistance depends on both the resistivity of the material and its physical dimensions.
Can we use this in real-life applications?
Absolutely! Understanding these principles helps in engineering applicationsβsuch as designing electrical wiring. Let's keep practicing these concepts!
Current Density and Drift Velocity
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now weβll dive into current density and drift velocity, which are intertwined with Ohm's Law. Can anyone define current density?
Isn't current density how much current flows per area?
Correct! Current density (j) is defined as j = I/A, where I is the current and A is the cross-sectional area. And now, drift velocityβany ideas?
Drift velocity is the average velocity of charge carriers in a conductor, right?
Exactly! We can relate these concepts using the equation j = n*q*v_d, where n is the number density of carriers, q is the charge, and v_d is the drift velocity. To remember: 'More density, more flow!' So, how do we connect drift velocity back to Ohm's Law?
If drift velocity is linked to the force on the carriers, then itβs influenced by the electric field?
Absolutely right! The force acting on the carriers due to the electric field leads to drift velocity, supporting the concept that current flows as electrons respond to voltage differences. Let's make sure to practice these relationships with examples.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Ohm's Law, formulated by Georg Simon Ohm, states that the voltage (V) across a conductor is proportional to the current (I) flowing through it, represented by the equation V = RI, where R is the resistance. This section explains how resistance varies with the dimensions of conductors and introduces other related concepts like resistivity and current density.
Detailed
Ohmβs Law
Ohm's Law is a foundational principle in electrical engineering that defines the relationship between voltage, current, and resistance. Formulated by Georg Simon Ohm in 1828, the law articulates that:
- Voltage (V) is proportional to the Current (I) flowing through a conductor, leading to the formula:
V = R Γ I
where R denotes the resistance of the conductor.
- The implications of Ohmβs Law extend beyond just the formula; resistance (R) is affected not only by the material of the conductor but also by its physical dimensions. For instance, increasing the length of a conductor results in increased resistance, while increasing its cross-sectional area decreases resistance. These relationships can be expressed mathematically as:
- R β l (length)
- R β 1/A (cross-sectional area)
Combining these factors leads to an expression for resistance in terms of the materialβs resistivity (Ο):
R = Ο(l/A)
The concepts of current density (j), defined as the current per unit area, and drift velocity (v_d), which describes the average velocity of charge carriers, are also intricately linked to Ohm's Law. The complete understanding of these concepts is crucial for exploring the behavior of electric currents in various materials and applications.
Overall, Ohm's Law not only simplifies the analysis of electric circuits but is also vital in predicting how different materials will behave when subjected to electric fields.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Ohm's Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A basic law regarding flow of currents was discovered by G.S. Ohm in 1828. Imagine a conductor through which a current I is flowing and let V be the potential difference between the ends of the conductor. Then Ohmβs law states that
V β I
or,
V = R I (3.3)
where the constant of proportionality R is called the resistance of the conductor. The SI units of resistance is ohm, and is denoted by the symbol W.
Detailed Explanation
Ohm's Law, formulated by Georg Simon Ohm, establishes a direct relationship between the voltage (V) across a conductor and the current (I) flowing through it. The equation V = RI indicates that the voltage is equal to the current multiplied by the resistance (R). This means that if you increase the voltage applied to a conductor, the current will also increase, provided the resistance remains constant. The unit of resistance is called an ohm (Ξ©).
Examples & Analogies
Think of Ohm's Law like water flowing through a hose: the voltage (V) is like the pressure of the water, the current (I) is like the amount of water flowing through per second, and the resistance (R) is like the size of the hose. If you increase the pressure, more water will flow, but if the hose is narrow (higher resistance), less water will flow even with the same pressure.
Factors Influencing Resistance
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The resistance R depends on the material of the conductor and the dimensions of the conductor. The dependence of R on the dimensions of the conductor can easily be determined as follows.
Consider a conductor satisfying Eq. (3.3) to be in the form of a slab of length l and cross section area A. ... Thus, doubling the length of a conductor doubles the resistance. In general, then resistance is proportional to length,
R β l (3.5)
Detailed Explanation
The resistance of a conductor not only depends on the material it is made from but also on its physical dimensions. Specifically, resistance increases with the length of the conductor: a longer conductor provides more material for electrons to collide with, increasing resistance. This can be mathematically represented by R proportional to l (the length of the conductor). Conversely, increasing the cross-sectional area (thickness) of the conductor decreases resistance, allowing more electrons to flow simultaneously.
Examples & Analogies
Imagine a long, skinny straw versus a short, wide straw. Water flows much easier through the wide straw than through the skinny one. Just like the water, electric current flows easier through a thicker conductor than a thinner one. If you make the skinny straw longer, it also becomes harder for the water to pass through, showcasing how resistance increases with length.
Ohm's Law and Resistivity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Combining Eqs. (3.5) and (3.7), we have
R β (l/A)
and hence for a given conductor
R = Ο(l/A)
where Ο is called resistivity.
Detailed Explanation
When you combine the relations for resistance with respect to length and area, you can express resistance in terms of resistivity and the dimensions of the conductor. Resistivity (Ο) is a property inherent to the material of the conductor, indicating how strongly it opposes the flow of electric current. Itβs measured in ohm-meters. The greater the resistivity, the higher the resistance will be for a given length and cross-sectional area of the material.
Examples & Analogies
If you're using different types of hoses to water your garden, some hoses may have material that restricts water flow more than others (like rubber compared to metal). The rubber hose has a higher resistivity, meaning it resists the flow of water more, similar to how a material with high resistivity would resist the flow of electric current.
Drift Velocity and Current Density
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Current per unit area (taken normal to the current), I/A, is called current density j. The SI units of the current density are A/mΒ². Further, if E is the magnitude of the uniform electric field in the conductor whose length is l, then the potential difference V across its ends is El. ... E = jΟ (3.12).
Detailed Explanation
Current density (j) gives an idea of how much current is flowing through a specific area of the conductor. You can think of it as the density of water flowing in a given section of a river. When a uniform electric field (E) is applied, it influences how electrons drift, leading to current density in the conductor. Ohmβs Law can also be expressed in terms of current density, illustrating the relationship between drift velocity, electric field, and resistivity.
Examples & Analogies
Imagine a crowded hallway. If a motivational speaker starts talking at one end, people might start moving toward the speaker. The number of people moving toward the speaker in a given section of the hallway can be thought of as current density. If the group becomes denser, more people are flowing through that section, similar to how more current can flow through a conductor under a stronger electric field.
Limitations of Ohm's Law
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
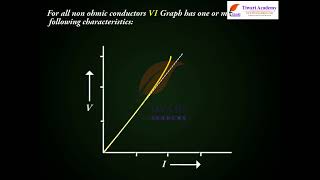
Although Ohmβs law has been found valid over a large class of materials, there do exist materials and devices used in electric circuits where the proportionality of V and I does not hold. ... (c) The relation between V and I is non-unique.
Detailed Explanation
While Ohmβs law is universally applicable in many scenarios, there are exceptions. For instance, in materials like diodes and transistors, the relationship between voltage and current is not linearβmeaning that the same voltage can produce different currents under different conditions. This indicates that resistors and non-ohmic devices do not follow Ohm's law consistently, limiting its applicability.
Examples & Analogies
Think of a light dimmer switch in a room. Turning the knob changes how bright the light is, but it doesnβt follow a simple linear path β you can have dim lights with a certain twist and brighter lights at subsequent twists without following a fixed ratio of voltage to current. This is an example of how, in some devices, increasing voltage doesnβt always result in a proportional increase in current.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Ohm's Law: Describes the relationship between voltage, current, and resistance.
-
Resistance: The opposition a material has to the flow of current.
-
Resistivity: A material property that affects resistance based on material dimensions.
-
Current Density: The amount of current flowing per unit area of a conductor.
-
Drift Velocity: The average speed of charge carriers in a conductor under an electric field.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If a 9V battery is connected across a 3Ξ© resistor, using Ohm's Law, the current through the resistor can be calculated as I = V/R = 9V/3Ξ© = 3A.
-
For a copper wire of length 2 m and cross-sectional area 1 mmΒ² with a resistivity of 1.68 Γ 10β»βΈ Ω·m, the resistance can be calculated as R = Ο(l/A) = 1.68 Γ 10β»βΈ Γ (2)/(1 Γ 10β»βΆ) = 0.0336 Ξ©.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Ohm's Law is the key, V equals I times R, you see!
π Fascinating Stories
-
Imagine a river: the voltage is the flow, the resistance is the rocks, and the current is how fast it goes.
π§ Other Memory Gems
-
VIR: Voltage = Current Γ Resistance.
π― Super Acronyms
RIV - Remember
- Resistance impacts Voltage and Current.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Ohm's Law
Definition:
The principle stating that the current flowing through a conductor is directly proportional to the voltage across it at constant temperature.
-
Term: Resistance (R)
Definition:
A measure of the opposition to current flow in an electrical circuit, measured in Ohms (Ξ©).
-
Term: Voltage (V)
Definition:
The electric potential difference between two points, measured in volts (V).
-
Term: Resistivity (Ο)
Definition:
An intrinsic property of a material that quantifies its opposition to current flow, measured in Ohm-meters (Ω·m).
-
Term: Current Density (j)
Definition:
The amount of electric current per unit area of cross-section, measured in amperes per square meter (A/mΒ²).
-
Term: Drift Velocity (v_d)
Definition:
The average velocity of charge carriers in a conductor due to an electric field.