Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Wheatstone Bridge
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're discussing the Wheatstone Bridge. Can anyone tell me what a bridge circuit is?
Isnβt it a circuit that helps measure resistance?
Exactly! It consists of four resistors arranged in a diamond shape. Why do you think knowing the value of one resistor is useful?
Because if we change one resistor, we can find the unknown one, right?
Right! This balance helps us find the unknown resistance by comparing it to known values. Letβs remember the key formula associated with the balanced state: R1/R2 = R3/R4. You can think of it as 'resistance ratio equals resistance ratio'βsimple!
Applying Kirchhoffβs Rules
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs apply Kirchhoffβs rules to our bridge. Does anyone remember the junction rule?
Yes! The currents entering a junction must equal those leaving.
Great! Now, if we know the currents in two branches, how can we express them in terms of each other in the bridge?
We can set them equal when the bridge is balanced, right? So, Ig = 0 when balanced.
Correct! Under this condition, we can derive the relationships for currents through the resistors using loop rule. For loop ABDA and BCDB, students will demonstrate this by writing down equations. Can you summarize the balance condition we derived?
R1/R2 = R3/R4, which tells us how the resistance ratio must match!
Perfect! This is fundamental for understanding how the Wheatstone Bridge functions.
Practical Applications of the Wheatstone Bridge
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, who can tell me how the Wheatstone Bridge is used practically?
We can use it to measure resistance accurately.
Right! One common device is the meter bridge. Can anyone connect this concept with a real-life application?
It can help calibrate measuring equipment!
Exactly! Such methods ensure accuracy in scientific experiments. Always remember the balance principle when working with circuits!
Example Problem: Calculating Current through a Galvanometer
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs solve an example together. Imagine we have a Wheatstone bridge with resistances 100Ξ©, 10Ξ©, 5Ξ©, and 60Ξ© and a galvanometer attached. How do we approach this?
First, we should set up the equations based on what we learned, right?
Yes! If we maintain a 10V difference across AC, we can calculate the current through the galvanometer. Letβs write the equations for the mesh. What do we start?
We write the mesh equations according to Kirchhoff's loop rule for BADB.
Correct. Letβs do the math and get to the current that passes through the galvanometer!
I got 4.87 mA!
Awesome! You applied the Wheatstone Bridge principles effectively!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
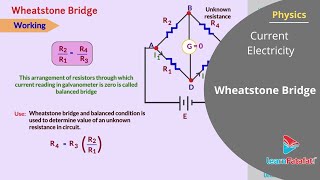
The Wheatstone Bridge consists of four resistors arranged to detect current through a galvanometer. When the bridge is balanced, the ratio of the resistances can be used to determine an unknown resistance based on known resistor values. The principles of Kirchhoff's rules are applied to analyze this circuit for both balanced and unbalanced conditions.
Detailed
Wheatstone Bridge: Detailed Overview
The Wheatstone Bridge is a significant measurement device in electrical circuits, particularly for determining the value of an unknown resistor by balancing two sides of the bridge with known resistors. In its basic form, the bridge comprises four resistors arranged in a diamond shape, with a galvanometer connected between two opposing vertices. The purpose is to find the condition under which no current flows through the galvanometer, indicating a balanced state.
Key Concepts:
- Balanced Bridge Condition: When the potential between the galvanometer terminals is zero (no current), it indicates that the ratio of the two resistances in one arm equals the ratio of the two in the other arm (i.e., R1/R2 = R3/R4).
- Use of Kirchhoffβs Laws: Kirchhoff's junction and loop rules are essential to derive these conditions and evaluate the currents and voltages across the resistors in the bridge.
- Meter Bridge: Practically, a common implementation of the Wheatstone Bridge is the meter bridge, which is used to measure unknown resistances very accurately.
The Wheatstone Bridge demonstrates fundamental concepts of electrical circuits, providing a method for accurate resistance measurement and exhibiting the applications of both Kirchhoffβs laws and the principles of balancing circuits.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Wheatstone Bridge Overview
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As an application of Kirchhoffβs rules consider the circuit shown in Fig. 3.18, which is called the Wheatstone bridge. The bridge has four resistors R1, R2, R3 and R4. Across one pair of diagonally opposite points (A and C in the figure) a source is connected. This (i.e., AC) is called the battery arm. Between the other two vertices, B and D, a galvanometer G (which is a device to detect currents) is connected. This line, shown as BD in the figure, is called the galvanometer arm.
Detailed Explanation
The Wheatstone bridge is a circuit configuration used to determine the unknown resistance in an electrical circuit. It consists of four resistors arranged in a diamond shape, with a voltage source connected across one diagonal and a galvanometer connected across the other diagonal. The key aspect of the Wheatstone bridge is to achieve a balance point where no current flows through the galvanometer, indicating a specific relationship between the resistances.
Examples & Analogies
Imagine you are trying to balance a scale. The Wheatstone bridge acts like a scale where you add known weights (R1 and R2) on one side and adjust an unknown weight (R4) on the other side until the scale levels out, showing no movement. At this point, you can determine the unknown weight using the weights of the known objects.
Balanced Bridge Condition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For simplicity, we assume that the cell has no internal resistance. In general, there will be currents flowing across all the resistors as well as a current I through G. Of special interest, is the case of a balanced bridge where the resistors are such that I g = 0. We can easily get the balance condition, such that there is no current through G.
Detailed Explanation
In a balanced Wheatstone bridge, the ratio of the resistances is such that there is no current through the galvanometer. Mathematically, this condition is expressed as R1/R2 = R3/R4, meaning that the resistances are in proportion. When this balance is achieved, the bridge can accurately measure the unknown resistance based on the known values.
Examples & Analogies
Consider a balanced seesaw. If both sides of the seesaw have equal weights and are positioned equally, it remains stable and horizontal, just like when the Wheatstone bridge is balanced, ensuring no current flows through the galvanometer.
Deriving the Balance Condition
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Thus the condition R1/R2 = R3/R4 relates the four resistors. This last equation relating the four resistors is called the balance condition for the galvanometer to give zero or null deflection. The Wheatstone bridge and its balance condition provide a practical method for determination of an unknown resistance.
Detailed Explanation
To find the unknown resistance R4, one can adjust the known resistors R1 and R2 until the galvanometer shows no deflection. At this point, the condition R1/R2 = R3/R4 holds true, allowing us to calculate the value of R4 based on the other resistances. This method is commonly used in laboratory settings to measure resistance accurately without directly connecting the unknown to a voltage source.
Examples & Analogies
Imagine a tuning fork being used to match the pitch of another fork. By adjusting the tension on the fork, you achieve a perfect match at a certain pitch. Similarly, by adjusting the known resistors in a Wheatstone bridge, you match the conditions until you can determine the unknown resistance accurately.
Practical Uses of the Wheatstone Bridge
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us suppose we have an unknown resistance, which we insert in the fourth arm; R4 is thus not known. Keeping known resistances R1 and R2 in the first and second arm of the bridge, we go on varying R3 till the galvanometer shows a null deflection.
Detailed Explanation
In practical applications, the Wheatstone bridge is widely used in measuring unknown resistances, calibrating measuring instruments, and even in temperature measurement through resistance thermometers. A common method involves inserting an unknown resistance in the fourth position of the bridge and adjusting the other resistors until the galvanometer zeroes out, allowing for precise determination of the unknown value.
Examples & Analogies
Think of a smartwatch that measures your heart rate. Just as the device calibrates certain parameters automatically for accuracy, the Wheatstone bridge calibrates resistors to provide accurate readings of unknown resistances in electric circuits.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Balanced Bridge Condition: When the potential between the galvanometer terminals is zero (no current), it indicates that the ratio of the two resistances in one arm equals the ratio of the two in the other arm (i.e., R1/R2 = R3/R4).
-
Use of Kirchhoffβs Laws: Kirchhoff's junction and loop rules are essential to derive these conditions and evaluate the currents and voltages across the resistors in the bridge.
-
Meter Bridge: Practically, a common implementation of the Wheatstone Bridge is the meter bridge, which is used to measure unknown resistances very accurately.
-
The Wheatstone Bridge demonstrates fundamental concepts of electrical circuits, providing a method for accurate resistance measurement and exhibiting the applications of both Kirchhoffβs laws and the principles of balancing circuits.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of constructing a Wheatstone Bridge to measure unknown resistance using resistors.
-
Example calculation of currents in a balanced Wheatstone Bridge circuit.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
To find the unknown, set the ratios right, With R1 and R2, make the balance tight.
π Fascinating Stories
-
Imagine a tightrope walker (the unknown resistor) using two fixed posts (known resistors) to keep their balance (the balanced bridge). They need to find their center to maintain stability, just like measuring resistance.
π§ Other Memory Gems
-
Rabbits Over Green Grass: R1/R2 = R3/R4 helps remember the Wheatstone balance condition.
π― Super Acronyms
BBS
- Balance Bridge Structure reminds us about Wheatstone Bridge function.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Wheatstone Bridge
Definition:
A circuit used to measure unknown resistances by means of a ratio of known resistors.
-
Term: Balance Condition
Definition:
The state in which no current flows through the galvanometer, indicating equal ratios of resistances.
-
Term: Kirchhoff's Laws
Definition:
Two laws dealing with the current and voltage in electrical circuits, used to analyze complex circuit behavior.
-
Term: Galvanometer
Definition:
An instrument used to detect and measure small electric currents.
-
Term: Resistances
Definition:
Elements in a circuit that oppose the flow of electric current.