Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Motional EMF
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Good morning class! Today we will discuss motional electromotive force, a vital concept in electromagnetism. Can anyone tell me what happens when a conductive material moves through a magnetic field?
I think it produces electricity?
Exactly, Student_1! This phenomenon is explained by Faraday's law of electromagnetic induction. The induced emf can be calculated using the formula \( e = Blv \), where B is the magnetic field strength, l is the length of the conductor, and v is its velocity. Let's break this down!
Why do we multiply those values?
Great question, Student_2! The multiplication helps capture the relationship between these factorsβindicating that higher speeds or stronger magnetic fields will increase the induced emf. Please remember the acronym 'B.E.L.V.' to recall these components!
Motional EMF Application: Generators
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's connect this to practical applications. One of the key uses of motional emf is in electric generators. How do you think motion is involved in generating electricity?
Is it something to do with rotating coils?
Absolutely, Student_3! A rotating coil within a magnetic field created by electromagnets induces an emf as it changes its orientation with respect to the field lines, thus generating electricity. It's a fascinating cycle of energy conversion!
So, without moving parts, can we still generate electricity?
In a way, yes! Static magnetic fields can induce emf in stationary conductors if the magnetic fields themselves vary with time. This is another key aspect of Faraday's law.
Calculating Induced EMF
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Alright class, letβs put our understanding into practice. If a 1-meter-long conductor moves through a magnetic field of 0.5 T at a velocity of 3 m/s, what is the induced emf?
Using the formula, it looks like \( e = 0.5 \times 1 \times 3 = 1.5 \) volts!
Exactly, Student_1! You've nailed it. Now imagine if we increased the velocity to 6 m/s, how much would the emf change?
It would be 3 volts this time!
Perfect! You've just demonstrated how increasing speed linearly increases the induced current. Keep practicing with different values.
Real-life Examples of Motional EMF
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now letβs discuss some real-life scenarios where motional emf plays a role. Can anyone name any such examples?
What about wind turbines?
Excellent, Student_3! Wind turbines indeed use motional emf principles, rotating blades within a magnetic field to generate energy. Any other examples?
Trains with magnetic levitationβthey probably use it too!
Great thinking! These applications highlight the versatility of motional emf in modern technology.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses how motional emf occurs when a conductor moves through a magnetic field, resulting in a change in magnetic flux and subsequent induced current. The laws governing this phenomenon, including the calculation of induced emf through motion, highlight the interplay between magnetic and electric fields, emphasizing practical applications in generators.
Detailed
Motional Electromotive Force
Motional electromotive force (emf) refers to the emf induced in a conductor moving through a uniform magnetic field. The section illustrates how the movement of a conductor in a magnetic field creates a change in magnetic flux, inducing an electric current within a circuit. This result aligns with Faradayβs law of electromagnetic induction, which states that the induced emf is directly proportional to the rate of change of the magnetic flux linked with the circuit.
Key Concepts:
- The induced emf results from the motion of the conductor across magnetic lines of force.
- The formula for calculating the induced emf (
\( e = Blv \)\) incorporates variables such as the strength of the magnetic field (B), the length of the conductor (l), and its velocity (v).
This interplay of velocity and magnetic field is crucial in the operation of electric generators, where mechanical energy is transformed into electrical energy, shaping modern electrical systems and devices.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Motional EMF
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
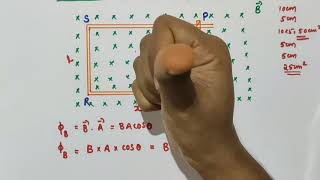
Let us consider a straight conductor moving in a uniform and time-independent magnetic field. Figure 6.10 shows a rectangular conductor PQRS in which the conductor PQ is free to move. The rod PQ is moved towards the left with a constant velocity v as shown in the figure. Assume that there is no loss of energy due to friction. PQRS forms a closed circuit enclosing an area that changes as PQ moves. It is placed in a uniform magnetic field B which is perpendicular to the plane of this system.
Detailed Explanation
In this section, we start by visualizing a straight conductor (a metal rod) that is moving within a magnetic field. Imagine the rod named PQ moving towards the left while a magnetic field, indicated by B, is acting perpendicular to the movement. This setup creates a closed circuit, which changes its area as the rod moves. When the area of a circuit changes in a magnetic field, it leads to the generation of electromotive force (emf), known as motional emf.
Examples & Analogies
Think about riding a bicycle with a small generator attached to the wheel. As you pedal and the wheel spins, the movement causes a conductor to move through the magnetic field inside the generator, producing electricity just like the movement of the rod PQ creates an emf. This principle is leveraged in things like dynamo systems used to power lights on bicycles.
Calculation of Induced EMF
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If the length RQ = x and RS = l, the magnetic flux \( \Phi \) enclosed by the loop PQRS will be \( \Phi = B l x \). Since x is changing with time, the rate of change of flux \( \Phi \) will induce an emf given by: \[ e = - \frac{d\Phi}{dt} = - \frac{d(Blx)}{dt} = -Blv. \]
Detailed Explanation
The flux through the loop changes as the rod moves, which we can express mathematically. The induced emf is based on this changing flux, and it's given by the equation \( e = -Blv \). Here, B is the magnetic field strength, l is the length of the rod, and v is the velocity with which the rod moves. The minus sign indicates the direction of the induced current, in accordance with Lenz's Law, which states the induced current opposes the change in magnetic flux.
Examples & Analogies
Imagine a water wheel that turns in a flowing river. As the wheel spins faster (analogous to the rod moving quickly through the magnetic field), it captures more energy from the water, leading to increased energy being produced. Similarly, the faster the rod moves, the greater the induced emf due to the changing area it sweeps in the magnetic field.
Lorentz Force and Work Done
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
It is also possible to explain the motional emf expression in Eq. (6.5) by invoking the Lorentz force acting on the free charge carriers of conductor PQ. Consider any arbitrary charge q in the conductor PQ. When the rod moves with speed v, the charge will also be moving with speed v in the magnetic field B. The Lorentz force on this charge is qvB in magnitude, and its direction is towards Q.
Detailed Explanation
The concept of Lorentz force comes into play when we look specifically at how individual electrical charges within the conductor respond to the magnetic field as the rod moves. Each charge experiences a force due to the magnetic field, which results in a separation of chargesβleading to the induced emf. The work done to move these charges is related to the induced emf, as the induced potential is essentially the energy per charge produced in the circuit.
Examples & Analogies
You can think of this like how pushing a child on a swing causes the swing to move. If you push harder (representing greater speed or more energy), the swing moves higher. Similarly, the more force exerted on the charges in the conductor due to the Lorentz force, the more emf is produced, like the energy exerted on that swing results in higher movement.
Induced EMF in Stationary Conductors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
On the other hand, it is not obvious how an emf is induced when a conductor is stationary and the magnetic field is changing β a fact which Faraday verified by numerous experiments. In the case of a stationary conductor, the force on its charges is given by \( F = q (E + v \times B) = qE \) since v = 0. Thus, any force on the charge must arise from the electric field term E alone.
Detailed Explanation
Here we explore a different scenario where the conductor remains stationary, but the magnetic field it is situated in changes. When the conductor does not move, the electric field generated needs to be addressed. Faraday demonstrated that during a changing magnetic field, an electric field is produced that exerts a force on the charges within the stationary conductor, thereby leading to induced emf.
Examples & Analogies
Think about a doorbell. When you push the button (the changing action), it creates an electrical signal that rings the bell (induced emf) even though the bell itself doesnβt move. Similarly, a changing magnetic field creates an 'electric push' on stationary charges, inducing an emf in the conductor.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
The induced emf results from the motion of the conductor across magnetic lines of force.
-
The formula for calculating the induced emf (
-
\( e = Blv \)\) incorporates variables such as the strength of the magnetic field (B), the length of the conductor (l), and its velocity (v).
-
This interplay of velocity and magnetic field is crucial in the operation of electric generators, where mechanical energy is transformed into electrical energy, shaping modern electrical systems and devices.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A 1-meter conductor moves at 3 m/s in a magnetic field of 0.5 T, resulting in an induced emf of 1.5 volts.
-
Electric generators use motional emf, with rotating coils inducing electrical currents.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
In fields of magnetic sway, a mover makes the current play!
π Fascinating Stories
-
Imagine a train moving quickly through a tunnel. The train is a conductor moving in a magnetic field, creating electricity!
π§ Other Memory Gems
-
B.E.L.V. β Magnetic Field Strength (B), length of Conductor (l), Velocity (v)
π― Super Acronyms
M.E.F. - Motional Electromotive Force
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Motional EMF
Definition:
The electromotive force induced in a conductor moving through a magnetic field.
-
Term: Magnetic Field (B)
Definition:
A field around a magnet where magnetic forces are exerted.
-
Term: Velocity (v)
Definition:
The speed and direction of a moving object or conductor.
-
Term: Faraday's Law of Induction
Definition:
A law stating that a changing magnetic field within a loop of wire induces an electromotive force in the wire.