Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Fundamentals of Sampling
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're going to discuss the fundamental concept of sampling. Can anyone tell me why sampling is critical in signal processing?
Isn't it about converting continuous signals into discrete ones?
Exactly! Sampling captures the signal value at specific intervals, transforming it from a continuous-time signal into a discrete-time signal. Itβs crucial for going from what we see visually in the time domain to something we can analyze numerically.
What happens if we sample too slowly?
Great question, Student_2! If we sample too slowly, we encounter aliasing, where higher frequency components become indistinguishable from lower ones. We will discuss this later in detail, but remember: 'Sample Right, Avoid Sight' can help us remember the importance of correct sampling rates.
Time and Frequency Domains
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs talk about the two perspectives we have on signals: the time domain and the frequency domain. Who can tell me the primary distinction between the two?
The time domain shows how a signal changes, and the frequency domain shows the frequencies that make up the signal?
Correct! The time domain gives us a view over time, while the frequency domain breaks the signal down into its constituent frequencies, revealing insights such as periodicities. If we want to remember this, we can think of 'Time Ticks, Frequencies Flick.'
So, both domains are needed for a complete understanding of a signal?
Absolutely, Student_4! They provide complementary views that enhance our analysis capabilities.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The introduction highlights the dual representations of signals in the time and frequency domains and sets the stage for a deeper exploration of sampling, reconstruction, and aliasing. These concepts are critical for accurate signal representation and processing.
Detailed
In the realm of signal processing, sampling, reconstruction, and aliasing serve as foundational concepts connecting continuous-time and discrete-time signals. This section elucidates the significance of time and frequency domain representations, which collectively provide a comprehensive view of a signal's characteristics. The time domain illustrates the evolution of a signal over time, while the frequency domain reveals its frequency components, thus allowing for the examination of periodicities and overall signal structure. Within this chapter, we will delve into how these principles influence the accuracy and fidelity of signal representation and processing across both domains. Understanding these concepts is crucial for anyone studying or working in fields related to signal processing.
Youtube Videos
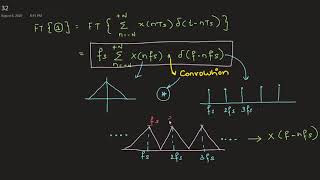
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Foundational Concepts in Signal Processing
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
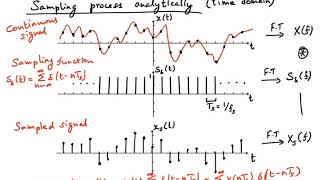
In signal processing, sampling, reconstruction, and aliasing are foundational concepts that bridge the gap between continuous-time signals and discrete-time signals.
Detailed Explanation
This introduction highlights three key concepts in signal processing: sampling, reconstruction, and aliasing. Sampling is the process of converting a continuous signal (which can take any value at any time) into a discrete signal (which is only defined at certain intervals). Reconstruction is the method of converting a discrete signal back into a continuous signal, preserving its original characteristics. Aliasing is the phenomenon that occurs when sampling is done inadequately, leading to misrepresentation of the signal's frequency components.
Examples & Analogies
Imagine you're taking photos of a moving car as it drives past. If you only take a photo every five seconds (low sampling rate), you might miss some key details, like the car's speed or direction. This is similar to sampling in signal processing β if you don't 'capture' the signal often enough, you lose important information about it.
Time and Frequency Domain Representations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A signalβs time and frequency domain representations provide complementary views of the same information. While the time domain represents how a signal evolves over time, the frequency domain represents the signal in terms of its frequency components, allowing for analysis of periodicities and signal structure.
Detailed Explanation
In signal processing, a signal can be examined in two different domains: the time domain and the frequency domain. The time domain representation shows how the signal changes over time, like a graph depicting a sound wave's amplitude at each moment. In contrast, the frequency domain shows what frequencies make up the signal. This analysis helps identify patterns or periodic elements in the signal, making it easier to understand how it behaves.
Examples & Analogies
Think of listening to music. When you hear a song, you're experiencing it in the time domain as you perceive the progression of sounds over time. If you analyze the song using software that displays frequencies, you're looking at the same song in the frequency domain, where you can see the different notes being played. Just like looking at the song from different perspectives gives you more understanding, looking at signals in both domains promotes better signal analysis.
The Focus of This Chapter
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In this chapter, we will explore the relationship between the time and frequency domains with respect to sampling, reconstruction, and aliasing. We will also discuss how these concepts impact the accuracy of signal representation and processing in both domains.
Detailed Explanation
The chapter sets out to investigate how sampling, reconstruction, and aliasing intertwine with the time and frequency representations of signals. It will detail how these concepts each play a vital role in ensuring that signals are represented accurately and processed effectively. Understanding these relationships is crucial for anyone working with signals, be it in audio processing, telecommunications, or any field relying on signal analysis.
Examples & Analogies
Imagine a chef preparing a new recipe. The chef needs to understand the interplay of ingredients (sampling), the process of cooking (reconstruction), and the outcome of the dish (aliasing). Each of these elements affects the final meal. Similarly, comprehending how sampling, reconstruction, and aliasing affect how we perceive signals allows us to work with them effectively, ensuring 'delicious' results in signal processing.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Sampling: Essential for converting continuous signals to discrete ones.
-
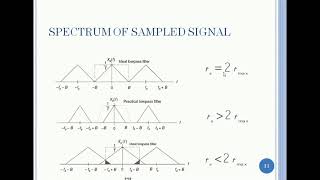
Aliasing: Occurs when high frequencies are misrepresented due to low sampling rates.
-
Time Domain: Illustrates how signals change over time.
-
Frequency Domain: Breaks down signals into their frequency components.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A sound wave recorded at 44.1 kHz captures frequencies up to approximately 22 kHz, adhering to Nyquist's theorem.
-
When a signal containing a 30 Hz wave is sampled at 40 Hz, aliasing occurs as the sampled data misrepresents high frequency components.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Sampling keeps it neat, avoids aliasing defeat.
π Fascinating Stories
-
Imagine a painter who takes quick snapshots of a sceneryβif he snaps too slowly, the moving clouds become indistinguishable from still ones, just as sampling captures a signal inaccurately if not done properly.
π§ Other Memory Gems
-
SAM - Sample and Avoid Misrepresentation.
π― Super Acronyms
FIFTY - Frequency Information Found Through Yonder (to remember the Nyquist theorem).
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Sampling
Definition:
The process of converting a continuous-time signal into a discrete-time signal by measuring its value at specific intervals.
-
Term: Reconstruction
Definition:
The process of restoring a continuous-time signal from its discrete-time samples, often using interpolation methods.
-
Term: Aliasing
Definition:
An effect that occurs when high-frequency signals are undersampled, causing distortion in the reconstructed signal as high frequencies overlap with lower frequencies.
-
Term: Time Domain
Definition:
A representation of a signal based on time, illustrating how the signal evolves over time.
-
Term: Frequency Domain
Definition:
A representation of a signal based on its frequency components, enabling the analysis of periodicities and overall structure.