Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Importance of Reconstruction
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're diving into the reconstruction of signals. Why do you think we need to reconstruct a continuous-time signal from discrete samples?
Is it to get back the original signal?
Exactly! When we sample a continuous signal, we create discrete-time samples, but we must reconstruct the signal for effective processing, especially in real-world applications.
What methods do we use for reconstruction?
Great question! The ideal method uses sinc function interpolation to reconstruct the original signal. The formula for reconstruction is important! Can someone tell me what the sinc function is?
It's \( sinc(x) = \frac{sin(\pi x)}{\pi x} \)!
Perfect! This helps us interpolate smoothly between the sampled points. Remember, we denote our reconstructed signal as \( x_r(t) \).
What happens if the reconstruction isn't ideal?
If the reconstruction isnβt handled properly, we can experience aliasing and distortion, which emphasizes the importance of using appropriate filters.
Letβs summarize: we reconstruct signals to get back to original forms and we primarily rely on sinc interpolation to achieve this. Remember, ideal reconstruction assumes no noise or distortion.
Practical Considerations in Reconstruction
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we understand the theoretical background, letβs discuss how it applies in real-world scenarios. In practice, perfect reconstruction may not be feasible. Why do we face these limitations?
I guess noise can affect the signal?
Correct! Noise and hardware imperfections can impair our ability to reconstruct signals accurately. What do we typically use to handle these issues?
Low-pass filters?
Yes! Low-pass filters help smooth out the signal and approximate the sinc function to mitigate distortion. Can someone summarize how these relate to our sampling frequency?
We need a high enough sampling rate to avoid aliasing, right?
Exactly! So we design our systems to ensure that we sample high enough to capture the necessary frequencies without introducing aliasing during reconstruction. Good job everyone!
Analyzing Practical Examples
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, letβs dig into examples. Suppose we sample an audio signal at a frequency that meets the Nyquist criterion. What can we expect during reconstruction?
We should be able to reconstruct the signal closely to the original?
Absolutely right! And if our sampling frequency is too low? What are the consequences?
We might experience aliasing!
Exactly! In this case, high-frequency components would distort the reconstructed signal. Can anyone suggest how we could use filters to improve reconstruction?
By applying an anti-aliasing filter before sampling?
Thatβs correct! This strategy ensures we capture the right frequency components effectively. As weβve discussed, real-world systems must be designed considering both sampling rates and reconstruction strategies.
Letβs recap this session: proper sampling rates are key to reducing distortion when weβre reconstructing signals, and filters play a crucial role in ensuring this.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
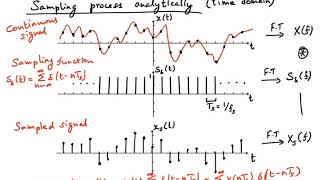
Reconstruction of a continuous-time signal from its discrete-time samples is crucial in signal processing. Ideal reconstruction is achieved through sinc function interpolation, ensuring that the reconstructed signal accurately reflects the sampled data points. In practical systems, low-pass filters approximate the ideal sinc function.
Detailed
Reconstruction from Samples
Reconstructing a continuous-time signal from discrete-time samples is a critical process in signal processing that ensures accurate signal representation after sampling. The ideal method of reconstruction utilizes the sinc function, an interpolation function defined as:
\[ sinc(x) = \frac{sin(\pi x)}{\pi x} \]
The reconstructed signal \( x_r(t) \) can be expressed mathematically as:
\[ x_r(t) = \sum_{n=-\infty}^{\infty} x[n] \cdot sinc\left( \frac{t - nT}{T} \right) \]
In this equation, \( x[n] \) represents the discrete samples, and \( T \) is the sampling period, serving to map the discrete data back to a continuous signal. The sinc function plays a vital role as it passes through each sample point and smoothly interpolates between them, giving rise to an accurate representation of the original continuous signal.
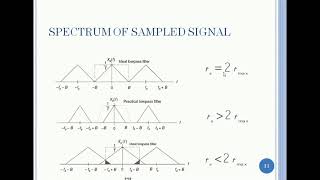
In practical applications, achieving perfect reconstruction is often unattainable due to inherent system limitations, noise, and other factors. As a result, low-pass filters are commonly employed to approximate the ideal sinc function during reconstruction. These filters help mitigate aliasing effects and reconstruct the signal as closely as possible to its original form without distortion.
Youtube Videos
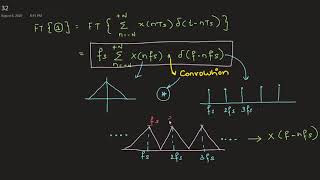
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Ideal Reconstruction with Sinc Function
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Reconstructing a continuous-time signal from its discrete-time samples involves using an interpolation process. Ideal reconstruction is achieved by using the sinc function interpolation. The reconstructed signal is given by:
xr(t)=βn=βββx[n]β
sinc(tβnTT)x_r(t) = _z}
Where:
β sinc(x)=sin (Οx)Οx\text{sinc}(x) = \frac{\sin(\pi x)}{\pi x} is the interpolation function.
β The sinc function ensures that the reconstructed signal passes through each sample point and smoothly interpolates between them.
Detailed Explanation
When we want to recreate a continuous-time signal from discrete samples, we need a way to fill in the gaps between these samples. An interpolation process is used for this purpose. The ideal method of interpolation uses the sinc function, which has a unique shape that can perfectly reconstruct the original signal if the samples are taken correctly.
Mathematically, the reconstructed signal can be represented as a sum of the samples multiplied by the sinc function evaluated at different time points. This means that each sample influences the reconstructed signal according to its distance from that point in time, allowing a smooth transition between the samples.
Examples & Analogies
Think of the sinc function as the behavior of a skilled painter. If you have discrete brush strokes (samples) on a canvas, the painter uses their brush (the sinc function) to blend the strokes together, creating a smooth image. Just like the painterβs brush fills in spaces and connects the colors, the sinc function helps connect the discrete samples so that the reconstructed signal looks seamless.
Practical Reconstruction with Filters
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In practical systems, reconstruction is done using filters (often low-pass filters) that approximate the ideal sinc function, but the ideal case assumes perfect reconstruction without aliasing.
Detailed Explanation
In real-world applications, achieving perfect reconstruction using the sinc function is not always possible due to various limitations. Therefore, engineers often use filters, particularly low-pass filters, to approximate the behavior of the sinc function. A low-pass filter allows low-frequency components to pass through while attenuating high-frequency components that might cause distortion. This approach helps to create a smoother signal that comes closer to what the original continuous-time signal would look like, although it may not be perfect.
Examples & Analogies
Imagine you are trying to remake a recipe from a dish you tasted before, but you don't have the exact ingredients. Instead, you choose the closest substitutes you can find in your pantry. While it might not taste exactly the same, with skill, you can approximate the original dish quite well. Similarly, the filters act as substitutes for the perfect sinc function during the reconstruction process, allowing us to get a close approximation of the original signal.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Reconstruction: Process of recreating a continuous signal from discrete samples.
-
Sinc Function: Used as an interpolation function for ideal signal reconstruction.
-
Aliasing: Occurs when the sampling rate is too low, leading to distortion in the reconstructed signal.
-
Low-Pass Filter: Used in practice to smooth out and reduce aliasing effects in reconstructed signals.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
After sampling a music track at a proper rate, using sinc interpolation can allow clear reproduction of the original sound.
-
When sampling a video signal, if a frame rate is too low, motion blur can occur during reconstruction.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Sinc and samples dance a tune, interpolate to make things bloom.
π Fascinating Stories
-
Once a sound was lost between peaks, it cried for help, for its shape it seeks. A function named Sinc came to the call, bringing the samples back, restoring them all.
π§ Other Memory Gems
-
R.A.S.P: Reconstructing (R) requires (A) aliasing awareness (A), sinc interpolation (S), and practical filters (P).
π― Super Acronyms
P.A.S.T
- Perfectly Achieving Signal Trueness β ensure sampling works accurately with filters.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Sinc Function
Definition:
An interpolation function defined as sinc(x) = sin(Οx) / (Οx) used in the reconstruction of signals.
-
Term: Reconstruction
Definition:
The process of creating a continuous-time signal from its discrete-time samples.
-
Term: Interpolation
Definition:
The method of using known data points to estimate values at other points.
-
Term: Aliasing
Definition:
A phenomenon where high-frequency signals become indistinguishable from low-frequency signals due to insufficient sampling.
-
Term: Lowpass Filter
Definition:
A filter that allows low-frequency signals to pass through and attenuates high-frequency signals, used in the context of reconstruction.