Sampling, Reconstruction, and Aliasing: Time and Frequency Domains
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Sampling
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Welcome class! Today, we'll talk about sampling. Can anyone tell me what sampling means in the context of signals?

Is it like taking a snapshot of a continuous signal at certain moments?

Exactly! Sampling converts a continuous-time signal into discrete-time by measuring its value at specified intervals. Does anyone know how we define those intervals?

I think it's based on the sampling period, right?

Very good! The sampling period, denoted as T, determines how often we take these samples. The frequency of sampling is the reciprocal, called the sampling frequency (fs). Remember, higher fs means more detail in our signal. What do you think might happen if we sample too slowly?

Maybe we miss some information? Like in aliasing?

Spot on! Aliasing occurs when high-frequency components overlap with lower frequencies due to insufficient sampling. Let’s conclude this session with a reminder: Always sample at a rate at least twice the highest frequency in the signal!
Understanding Aliasing and the Nyquist Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

In our last session, we discussed sampling. Now, let’s dive deeper into aliasing. Who can explain what aliasing is?

Aliasing happens when the sampling rate is too low, causing distortion in the reconstructed signal.

Exactly! According to the Nyquist Theorem, to avoid aliasing, we must sample at least at twice the highest frequency in our signal. This critical frequency is called the Nyquist frequency. Can anyone tell me why this is important in practice?

If we don't, we can lose valuable high-frequency information, making the signal look incorrect?

Right! If frequencies above the Nyquist frequency are present, they fold back and distort our perception of the signal. Always remember: 'Sample twice to maintain your voice!' As a mnemonic!
Reconstruction of Signals
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s discuss how we can reconstruct a continuous-time signal from its discrete samples. What do you think is the best way to do this?

I believe we use interpolation, and the sinc function is the ideal interpolation method.

Great! The sinc function interpolates between our sampled points smoothly. Can anyone tell me how the reconstruction formula looks?

I think it’s something like xr(t) = sum of x[n] times sinc(t - nT)?

Exactly! And remember, while perfect reconstruction is theoretically possible using sinc function, practical systems rarely achieve this perfection. They often use filtering. What happens if our reconstruction isn't good?

The signal would sound distorted or lose quality!

Right! Quality of reconstruction depends heavily on the sampling rate and filter used. That's key to signal processing.
Fourier Transform Overview
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's turn our attention to frequency analysis now. Who can explain the Fourier Transform and its role?

It transforms a signal from the time domain to the frequency domain, helping us analyze its frequencies?

Exactly! With Fourier Transform, we can see how much of the signal consists of various frequency components. What is the formula for the Fourier Transform of a continuous signal?

It’s X(f) equals the integral of x(t) times e to the minus j2πft, right?

Perfect! And for discrete signals, we use the Discrete Fourier Transform. Why do you think we prefer FFT for DFT?

Because it's way faster, especially for large datasets!

That's correct! The efficiency of FFT makes it essential for real-time signal processing.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section explains how sampling transforms continuous-time signals into discrete-time signals. It presents the principles of the Fourier Transform and Discrete Fourier Transform for frequency analysis, outlines the Nyquist theorem to prevent aliasing during sampling, and discusses the reconstruction of signals from samples. The importance of understanding these concepts in accurate signal representation is emphasized.
Detailed
Detailed Summary
In signal processing, sampling refers to the process of converting a continuous-time signal into a discrete-time signal by capturing its values at regular intervals, defined by the sampling period (T). The discrete-time signal is represented as a sequence of samples, which is essential for digital processing. The relationship between continuous-time and discrete-time signals is mathematically modeled, emphasizing how important the sampling frequency (
fs
) and Nyquist rates are to accurately capturing signal information, avoiding aliasing.
Fourier Transform is introduced as a method to analyze both continuous and discrete signals in the frequency domain, allowing insights into the signal's frequency content. The Continuous Fourier Transform provides a connection between time and frequency domains, while the Discrete Fourier Transform (DFT) converts discrete samples back into the frequency domain efficiently using algorithms such as the Fast Fourier Transform (FFT).
The section discusses aliasing, which occurs when a signal is sampled at a rate lower than twice its highest frequency (Nyquist frequency), causing higher frequencies to masquerade as lower ones. To avoid this, proper sampling rates should be maintained, along with using anti-aliasing filters before sampling. The reconstruction of the signal after sampling is also addressed, typically using interpolation methods, including the sinc function, to ensure that the signal is accurately reconstructed without distortion.
Overall, understanding these concepts in sampling, reconstruction, and aliasing is critical as they have profound impacts on signal representation and processing.
Youtube Videos

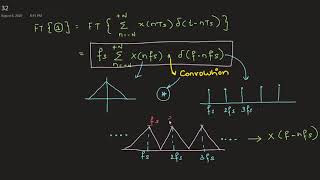
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Signal Processing Concepts
Chapter 1 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In signal processing, sampling, reconstruction, and aliasing are foundational concepts that bridge the gap between continuous-time signals and discrete-time signals. A signal’s time and frequency domain representations provide complementary views of the same information. While the time domain represents how a signal evolves over time, the frequency domain represents the signal in terms of its frequency components, allowing for analysis of periodicities and signal structure. In this chapter, we will explore the relationship between the time and frequency domains with respect to sampling, reconstruction, and aliasing. We will also discuss how these concepts impact the accuracy of signal representation and processing in both domains.
Detailed Explanation
This introduction sets the stage for understanding signal processing by defining three critical concepts: sampling, reconstruction, and aliasing. Sampling is the process of converting a continuous signal into discrete samples. Reconstruction refers to the process of turning those discrete samples back into a continuous signal, while aliasing is an issue that occurs when a signal is not sampled correctly. The time domain and frequency domain are two different ways to represent a signal. The time domain shows how a signal changes over time, while the frequency domain breaks a signal down into its component frequencies, allowing us to analyze its structure and periodicities.
Examples & Analogies
Think of sampling like taking snapshots of a moving object. If you take a photo every second (sampling frequency), you get a good idea of the object's motion. However, if you only take a photo every five seconds, you might miss important details of its movement, akin to how improper sampling can lead to aliasing.
Discrete-Time Signal Representation
Chapter 2 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
A continuous-time signal x(t) is represented as a sequence of discrete-time samples x[n] when sampled at a uniform rate fs (samples per second). The discrete-time signal is given by:
x[n]=x(nT)
Where:
● T is the sampling period, T=1/fs, and fs is the sampling frequency.
● x[n] is the value of the continuous signal at time t=nT, where n is an integer.
Detailed Explanation
This chunk explains how a continuous-time signal is converted into a discrete-time signal. When you sample a continuous signal at specific intervals, you get a sequence of values that can be indexed, represented by x[n]. The sampling period, T, is the time interval between samples, and the sampling frequency, fs, indicates how many samples are taken per second. This conversion is essential for digital signal processing, as computers handle discrete data rather than continuous signals.
Examples & Analogies
Imagine you’re recording a video of a performance. Each frame of the video captures the scene at a specific moment. The sampling period (T) would be the duration between each frame. If you record at 30 frames per second (fs), you can see the performance clearly, but if you only record 5 frames per second, you might not capture the full action.
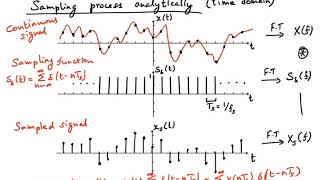
Understanding the Sampling Process
Chapter 3 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Sampling is the process of converting a continuous-time signal into a discrete-time signal by measuring the signal at specific intervals. Mathematically, this is done by multiplying the continuous signal by a periodic impulse train (a series of Dirac delta functions spaced by T):
xs(t)=x(t)⋅∑n=−∞∞δ(t−nT)
Where:
● δ(t−nT) is the Dirac delta function, indicating the sampling instances at t=nT. This produces a discrete-time signal x[n], where each sample corresponds to the value of the signal at specific times.
Detailed Explanation
In this section, the sampling process is described mathematically. Sampling involves taking the continuous signal and 'picking out' values at regular intervals, which is represented by the summation of Dirac delta functions. Each delta function corresponds to a specific sampling instance, and when you multiply the signal by this series, you extract values from the continuous signal, creating a discrete-time representation (x[n]).
Examples & Analogies
Think of sampling like picking apples from a tree. If you only pick apples at certain heights (sampling intervals), you are creating a limited view of all the apples that are actually there. The delta functions are like your hands, choosing which apples to grab based on their position in time (the tree).
Frequency Domain and Fourier Transform
Chapter 4 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The frequency domain provides a representation of a signal in terms of its frequency components, showing how much of the signal is composed of different frequencies. Fourier analysis transforms a signal from the time domain into the frequency domain, enabling us to analyze the signal’s periodic components.
Detailed Explanation
This section introduces the frequency domain, which facilitates the analysis of signals based on their frequency content rather than their time evolution. The Fourier transform is a mathematical tool that converts a time-domain signal (x(t)) into its frequency-domain representation (X(f)). This transform allows signals to be expressed as a combination of sinusoidal functions, each with different frequencies and amplitudes. This is particularly useful for identifying dominant frequencies within a signal.
Examples & Analogies
If you've ever played in a band, you might understand that each instrument produces sound at varying frequencies. The Fourier transform is like a magical tool that helps you figure out which instrument is playing which note, breaking down the entire sound into its components.
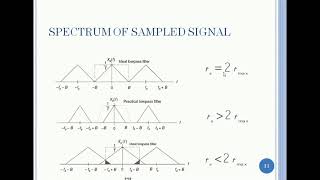
Aliasing in the Frequency Domain
Chapter 5 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Aliasing occurs when the sampling rate is too low to capture the signal's high-frequency components. In the frequency domain, aliasing is manifested as the overlapping of frequency components due to insufficient sampling. If a signal contains frequency components higher than half the sampling rate (the Nyquist frequency), these components will overlap with lower frequencies when sampled. This overlap leads to aliasing, where the high-frequency components are indistinguishable from lower-frequency components, causing distortion in the reconstructed signal.
Detailed Explanation
This section explains aliasing, a significant problem in signal sampling. When the sampling rate is lower than required (below the Nyquist frequency), higher frequency components of a signal can overlap with lower frequencies, resulting in an inaccurate representation. This produces an effect where the reconstructed signal has distortions, as some high-frequency information is misinterpreted as lower frequencies.
Examples & Analogies
Imagine trying to watch a poorly recorded movie where the camera moved too fast, causing the image to blur. Just like that blurred image, if we don't sample a signal fast enough, important details can 'blur' together and lead to a confusing result.
Reconstruction from Samples
Chapter 6 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Reconstructing a continuous-time signal from its discrete-time samples involves using an interpolation process. Ideal reconstruction is achieved by using the sinc function interpolation. The reconstructed signal is given by:
xr(t)=∑n=−∞∞x[n]⋅sinc(t−nT)
Where:
● sinc(x)=sin (πx)/πx is the interpolation function. The sinc function ensures that the reconstructed signal passes through each sample point and smoothly interpolates between them.
Detailed Explanation
This section details how a signal can be accurately reconstructed from its discrete samples using interpolation, particularly the sinc function. This mathematical function helps fill in values between the samples, enabling a smooth representation of the original continuous signal, assuming no aliasing occurred during the sampling process. The formula highlights that the reconstruction process is a summation over all samples to produce a continuous signal.
Examples & Analogies
Consider a bridge built over several pillars (samples). The sinc function acts like the material that fills in the gaps between those pillars, ensuring that the bridge is smooth and continuous, providing a travel path without any bumps or holes.
Practical Considerations: Sampling Rate and Signal Representation
Chapter 7 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Choosing a Sampling Rate: The sampling rate should be high enough to capture the frequency content of the signal without aliasing. In practice, the Nyquist rate is used as a guideline, but often a higher rate is chosen to ensure that the system can handle noise and other imperfections.
Anti-Aliasing Filter: An anti-aliasing filter (typically a low-pass filter) is applied before sampling to remove high-frequency components that might cause aliasing. This ensures that the signal being sampled contains only frequencies within the Nyquist range.
Signal Reconstruction: In practical systems, ideal reconstruction is not possible, and a low-pass filter is used to approximate the ideal sinc interpolation. The quality of reconstruction depends on the filter characteristics and the sampling rate.
Detailed Explanation
This chunk emphasizes practical aspects of sampling in real-world systems. It discusses the importance of choosing an appropriate sampling rate that exceeds the Nyquist rate to avoid aliasing. It also highlights the use of anti-aliasing filters to remove high-frequency noise prior to sampling, ensuring a clean signal. Lastly, it acknowledges that while ideal reconstruction isn't possible in practice, filters can be utilized to get as close to ideal reconstruction as feasible, and the quality of these filters significantly affects the outcome.
Examples & Analogies
Imagine planning a recording of a concert. You want to ensure that your microphone records at a high enough quality (sampling rate) so that you capture all the music clearly without distortion. Before the recording, you may need a filter to cut off any loud high-frequency sounds (anti-aliasing) that could mess up the sound, just like adjusting a camera to avoid overexposing bright lights.
Key Concepts
-
Sampling: The process of converting continuous signals into discrete signals at specific intervals.
-
Aliasing: The distortion resulting from undersampling high-frequency signals.
-
Nyquist Frequency: The maximum frequency that can be sampled without introducing errors.
-
Fourier Transform: A method to analyze signals in the frequency domain, decomposing them into frequency components.
-
Reconstruction: The process of rebuilding a continuous signal from its discrete samples.
Examples & Applications
Example 1: Sampling a sine wave at various rates shows how lower sampling leads to aliasing, while higher rates maintain the signal's integrity.
Example 2: Using the Fourier Transform on a sampled square wave reveals the fundamental frequency and its harmonics.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Sample twice to hear it right, or alias might blur your light.
Stories
Imagine a photographer who snaps pictures of moving cars at a slow rate—they miss crucial moments, leading to blurry images, akin to how sampling too slowly results in aliasing.
Memory Tools
SAM (Sampling, Aliasing, Max frequency) remind us of the three key aspects of this chapter.
Acronyms
N.F. = Nyquist Frequency = ½ Sampling Rate.
Flash Cards
Glossary
- Sampling
The process of converting a continuous-time signal into a discrete-time signal by capturing its value at regular intervals.
- Aliasing
The distortion that occurs when high-frequency components are misrepresented as lower frequencies due to insufficient sampling.
- Nyquist Frequency
Half of the sampling rate; defines the maximum frequency that can be accurately sampled without aliasing.
- Fourier Transform
A mathematical transform that decomposes a signal into its constituent frequencies, allowing for frequency domain analysis.
- Sinc Function
An interpolation function used in reconstructing continuous signals from discrete samples.
- Discrete Fourier Transform (DFT)
A mathematical technique that transforms discrete-time signals into their frequency domain representation.
Reference links
Supplementary resources to enhance your learning experience.
