Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Degrees of Freedom
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Welcome, everyone! Let's begin with the basic concept of Degrees of Freedom, or DOF, in structural engineering. Can anyone tell me what a degree of freedom refers to?
Is it about how a structure can move?
Exactly! A degree of freedom refers to the minimum number of independent coordinates needed to describe the motion of a system. In structural terms, this often relates to the displacements a structure can undergo.
What types of movements does it include?
Great question! We have translational movements along the x, y, or z axes, and rotational movements around these axes. Additionally, some structures may experience coupled DOFs, especially if they are irregular.
How does that affect earthquake engineering?
The complexity of structural analysis increases with the number of degrees of freedom. It shapes our understanding of natural frequencies and mode shapes, which is crucial during seismic events.
So, why do we need to simplify to SDOF systems?
Simplifying to Single-Degree-of-Freedom systems helps us grasp fundamental behaviors before analyzing more complex models. It’s a stepping stone to understanding dynamic responses!
In summary, Degrees of Freedom are essential for defining structural movement, crucial in seismic analysis, and we're going to see how SDOF systems play a key role in that. Moving on, let’s talk more about dynamic degrees of freedom!
Dynamic Degrees of Freedom
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s dive deeper into dynamic degrees of freedom. Who can tell me how these differ from static degrees of freedom?
Are they the same as regular DOF but for moving loads?
That's spot on! Dynamic degrees of freedom refer to the coordinates that dictate a structure's motion under dynamic loads, like those from earthquakes. We need to analyze them carefully.
How do we determine the number of dynamic DOFs?
To determine dynamic DOFs, we look at the structure’s geometry, identify displacement points, and apply constraints and supports. For instance, a cantilever beam primarily has one dynamic DOF related to lateral displacement.
What about more complex structures?
Multi-story frames will have multiple lateral DOFs because each floor can move independently. This highlights the need for careful modeling in dynamic analysis.
In conclusion, understanding dynamic degrees of freedom is pivotal for accurate seismic analysis and allows us to model complex behaviors effectively.
Single-Degree-of-Freedom System
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Fantastic questions! Let’s shift to Single-Degree-of-Freedom systems. Can anyone explain what an SDOF system is?
It's a system that can be described by a single coordinate, right?
Precisely! An SDOF system simplifies complex motions into one variable, usually lateral displacement. They're essential in dynamic analysis.
What are its main components?
SDOF systems consist of a mass, representing inertia, a stiffness component that dictates restoring forces, and optionally damping, which dissipates energy. Together, they form the foundational elements of our analysis.
How do we derive the equations of motion for these systems?
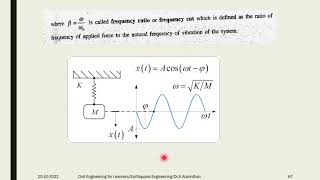
For an undamped SDOF, we use the equation: mu¨(t) + ku(t) = -mu¨(t)g. This shows the acceleration due to ground motion.
What about when damping is included?
Good observation! With damping, it becomes mu¨(t) + cu˙(t) + ku(t) = -mu¨(t)g. Damping alters system response, making it crucial for accurate simulations.
In summary, SDOF systems offer a simplified yet powerful tool for analyzing dynamic responses, enabling us to focus on critical behaviors in seismic design.
Limitations of SDOF Idealization
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Having discussed SDOF systems, let's now explore their limitations. Why might relying solely on SDOF modeling be problematic?
Because real buildings are often more complex than a single mode?
Exactly! SDOF idealization oversimplifies structural behavior, assuming all vibrations occur in a single mode, which isn’t always true. This neglects multi-modal responses.
What about buildings with eccentric mass or stiffness?
Excellent point! Such buildings may experience significant torsional effects that an SDOF model can't capture, potentially leading to critical failures during earthquakes.
So, it’s like an oversimplification?
Yes, precisely! Additionally, SDOF models do not account for localized deformations or failures in different parts of a structure. Thus, while SDOF models are invaluable, relying on them in isolation can lead to underestimations of structural responses.
To summarize, while SDOF systems are useful for initial analyses, recognizing their limitations is equally important when designing for seismic events.
Applications of SDOF Systems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we have a clear understanding of SDOF systems and their limitations, can anyone share where SDOF systems are commonly applied in engineering?
I think they’re used in designing response spectra?
Absolutely! Design response spectra are derived using SDOF models, providing quick estimations of seismic demand on structures. This is a significant practical application.
What about in testing dampers or isolation devices?
Exactly! SDOF models aid in evaluating energy dissipation capacities in devices like viscous dampers before they’re integrated into more complex systems.
Do we use them in time history analysis?
Great observation! Time history analyses often utilize SDOF systems to apply numerical solutions for seismic loads on structures, allowing for better understanding of dynamic responses.
In summary, SDOF systems are foundational tools in seismic design, providing insight for various applications while ensuring we maintain awareness of their limitations.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Degrees of Freedom (DOF) are critical for understanding the motion of structures in earthquake engineering. This section explores various types of DOF, the formulation of single-degree-of-freedom (SDOF) systems, their applications, and limitations, emphasizing the importance of this idealization in structural analysis and design.
Detailed
In structural engineering and particularly earthquake engineering, Degrees of Freedom (DOF) refer to the minimum number of independent coordinates necessary to describe the motion of a system. This section elaborates on definitions and types of DOF, including translational and rotational aspects, as well as their implications for structural analysis during seismic events. Emphasis is placed on Single-Degree-of-Freedom (SDOF) systems, which simplify the modeling process by aggregating structural behavior into a single motion variable. A detailed examination of the formulation of SDOF systems, including the equation of motion for damped and undamped systems, is presented. The section also highlights the appropriate scenarios for idealizing structures as SDOF and discusses the limitations of this approach in capturing complex structural behaviors during earthquakes. The relevance of SDOF systems as foundational tools in seismic design and analysis is underscored, providing a comprehensive understanding of their application and significance.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Degrees of Freedom (DOF)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In the context of earthquake engineering, the concept of degrees of freedom (DOF) plays a foundational role in structural modeling and analysis. The accurate representation of structural behavior under seismic forces begins with understanding how a structure can move—this is captured through its degrees of freedom. For many analysis methods, particularly in dynamic analysis, simplifying complex structures into single-degree-of-freedom (SDOF) systems helps in understanding fundamental behavior before extending to more realistic models.
Detailed Explanation
Degrees of freedom (DOF) define the possible movements a structure can make. In engineering, this means we need to know how the building might sway or flex when forces, like earthquakes, act on it. By simplifying complex structures into single-degree-of-freedom (SDOF) systems, engineers can first understand the basic patterns of movement before dealing with more complicated designs. This simplification helps in creating accurate models that respond to seismic activities.
Examples & Analogies
Think of a swing at a playground. It can move back and forth in one direction (forward and backward), which is similar to a single-degree-of-freedom system. Now imagine a complex ride with multiple swings and movements in different directions; it’s much harder to predict how it will react to someone jumping on it. Similarly, understanding one simple movement first helps us analyze the complex reactions of a structure during an earthquake.
Definition of Degrees of Freedom
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A degree of freedom refers to the minimum number of independent coordinates required to define the motion of a system. In structural engineering, this typically relates to possible displacements (translational or rotational) that a structure can experience.
Detailed Explanation
In structural engineering, a degree of freedom relates to the movement options available to a structure. It identifies how many ways a structure can move independently. For example, if a simple beam can only move up and down, that counts as one degree of freedom. If it can twist or sway as well, then that adds to its degrees of freedom. Understanding these movements allows engineers to predict how structures will behave under stress.
Examples & Analogies
Imagine a puppet on strings. It can move in various directions—up and down, side to side, and even twist. Each of these movements represents a degree of freedom. If you were to control the puppet, knowing how many ways it can move helps you direct it correctly, similar to how engineers predict structural behavior.
Types of Degrees of Freedom
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Translational DOF: Movement along x, y, or z directions.
• Rotational DOF: Rotation about x, y, or z axes.
• Coupled DOFs: Some structural systems exhibit coupling between translation and rotation, especially in irregular or torsionally unbalanced buildings.
Detailed Explanation
Degrees of freedom can be broken down into different types. Translational degrees of freedom refer to linear movements along specific axes—up/down, left/right, or forward/backward. Rotational degrees of freedom involve the ability to rotate around these axes. Coupled degrees of freedom occur in more complex structures where movement in one direction can affect movement in another direction—like when a building twists and sways during an earthquake. Differentiating these types helps engineers analyze how structures will react under various conditions.
Examples & Analogies
Think of a steering wheel in a car. When you turn the wheel (rotational DOF), the car moves in a direction (translational DOF). In certain terrains, such as icy roads, turning the wheel may cause the car to slide sideways (coupled DOFs). Understanding each type of movement helps engineers ensure vehicles remain stable on the road.
Importance of DOF in Earthquake Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Determines the complexity of structural analysis.
• Influences the natural frequencies and mode shapes.
• Helps in selecting appropriate numerical methods (modal analysis, time history, etc.).
Detailed Explanation
In earthquake engineering, understanding degrees of freedom is crucial. It sets the scene for how complex the analysis will need to be. More degrees of freedom usually mean more complex calculations, which can affect how engineers predict the building's behavior during earthquakes. It also impacts the natural frequencies of the building—how quickly it vibrates when hit by seismic waves—and the shape it takes while rocking back and forth, which is essential for safety. Having this knowledge helps in choosing the right analysis techniques to ensure buildings can withstand seismic activity.
Examples & Analogies
Imagine tuning a musical instrument like a guitar. The strings resonate at different frequencies; if you pluck one string (analogous to a degree of freedom), it vibrates and creates sound. If a string is not tuned properly, the music will sound off. Similarly, if engineers don’t understand and properly account for DOF, the structure may not be safe during an earthquake, just like a guitar that doesn’t sound right.
Dynamic Degrees of Freedom
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Dynamic degrees of freedom are those coordinates which define the motion of a structure due to dynamic (time-varying) loads such as seismic ground motion.
Detailed Explanation
Dynamic degrees of freedom refer to how a structure moves when subjected to forces that change over time, like an earthquake. Unlike static loads that are constant, dynamic loads fluctuate, creating different responses in the structure. Identifying these dynamic degrees of freedom is essential for engineers as they model how the building will behave during these specific conditions, enabling them to design more resilient structures.
Examples & Analogies
Think about a dancer performing a routine with choreography. During practice, the movements (dynamic loads) may change based on the beat and rhythm (time-varying conditions). Each position and transition the dancer makes represents a dynamic degree of freedom, helping to visualize how a structure reacts during changing conditions, similar to buildings swaying during an earthquake.
Determination of Dynamic Degrees of Freedom
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To identify the number of dynamic DOFs:
• Examine the geometry of the structure.
• Identify possible independent displacement points.
• Apply constraints and supports.
Detailed Explanation
Determining the number of dynamic degrees of freedom involves assessing the building's shape, finding points that can move independently, and understanding how different constraints (like walls or columns) restrict movements. Engineers must consider each of these elements to accurately gauge how many dynamic DOFs a structure possesses, which aids in creating effective models for analysis.
Examples & Analogies
Imagine a room full of furniture. If you want to rearrange the room without running into obstacles, you first need to figure out how much space you have (geometry), where each piece can be moved independently (displacement points), and how the walls (constraints) guide where you can place the furniture. This analogy illustrates how engineers analyze buildings to determine their dynamic response.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Degrees of Freedom (DOF): Refers to the independent coordinates needed to describe a structure's movement.
-
Single-Degree-of-Freedom (SDOF) System: A model that simplifies structural analysis by representing motion with a single variable.
-
Dynamic Degrees of Freedom: The coordinates that define motion due to dynamic loads, essential in understanding responses to seismic forces.
-
Lumped Mass Idealization: A modeling simplification that assumes mass is concentrated at discrete points.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a cantilever beam, the only significant dynamic DOF may be the lateral displacement at the top.
-
A multi-story frame building where each floor can move independently showcases multiple degrees of freedom.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Degrees of freedom tell a story, one motion at a time can bring us glory.
📖 Fascinating Stories
-
Imagine a dancer, moving freely through the air—some steps are forward, some are turns. Their graceful movement mirrors how structures sway in an earthquake.
🧠 Other Memory Gems
-
D.O.F. = Degrees Of Flexibility – remember how structures can flex in different directions.
🎯 Super Acronyms
SDOF = Single Dynamic Object Function – think of it as one core motion.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Degrees of Freedom (DOF)
Definition:
The minimum number of independent coordinates necessary to describe the motion of a system.
-
Term: SingleDegreeofFreedom (SDOF) System
Definition:
The simplest dynamic model where the motion can be described using a single coordinate, typically lateral displacement.
-
Term: Translational DOF
Definition:
Degrees of freedom related to movement along the x, y, or z directions.
-
Term: Rotational DOF
Definition:
Degrees of freedom related to rotation around the x, y, or z axes.
-
Term: Coupled DOFs
Definition:
Degrees of freedom that exhibit a coupling between translation and rotation, often seen in irregular structures.
-
Term: Dynamic Degrees of Freedom
Definition:
Coordinates defining the motion of a structure due to dynamic loads such as seismic ground motion.
-
Term: Lumped Mass
Definition:
A simplification that assumes mass is concentrated at specific points, commonly at floor levels.
-
Term: Natural Frequency
Definition:
The frequency at which a system tends to oscillate in the absence of any driving force.