Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Concept of Lumped Mass Idealization
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we're discussing Lumped Mass Idealization. This concept helps us simplify the modeling of structures during dynamic analysis by concentrating mass at certain points. Who can tell me where we typically assume this mass is concentrated?
Is it usually concentrated at the floor levels?
Exactly! Great job! We often lump mass at the floors because this helps to simplify complex structures. Now, why do we assume that floors are rigid in their own plane?
Because it makes the analysis easier and more straightforward?
Yes, assuming floors are rigid leads to a more efficient analysis. This is particularly useful in buildings with high stiffness. Can anyone think of examples where we might apply this method?
In modal analysis and response spectrum analysis?
Correct! Those are two of the principal analyses where we utilize the lumped mass model.
To recap, Lumped Mass Idealization simplifies complex structures by concentrating mass at floors, aiding various dynamic analyses.
Justification and Importance of LMI
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's talk about the justifications for using Lumped Mass Idealization. Why do you think it's acceptable in buildings with high floor stiffness?
It probably reflects the actual behavior of the structure without complicating the analysis too much?
Exactly! The assumption holds well when high stiffness results in minimal deformation. This simplification aids significantly in analyzing seismic responses effectively.
So, using lumped mass models helps reduce complexity in computations?
Yes, that's an important aspect. These models also illuminate fundamental behaviors under dynamic loads. Can you think of any downsides to this idealization?
Maybe it wouldn't be accurate for more flexible or irregular buildings?
Exactly! Lumped mass models may not suit all buildings, particularly those exhibiting complex behaviors. It’s crucial to know when this idealization is valid.
In summary, LMI is justified in high-stiffness systems and simplifies complex structural analysis while highlighting vital dynamic behaviors.
Applications and Significance of LMI
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's discuss where we typically apply lumped mass models. Can anyone suggest some specific applications?
I think modal analysis would be one, right?
Absolutely, modal analysis is crucial! What else?
Time history analysis is another application.
Yes! And also response spectrum analysis. These applications enhance our understanding of seismic behavior. Why is this understanding significant?
It helps in designing structures that can withstand earthquake forces better.
Exactly! Understanding the foundational behaviors allows engineers to design safer buildings. Summarizing, lumped mass idealization applies predominantly in modal analyses and helps improve seismic design.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The lumped mass idealization refers to the practice of modeling the mass of a structure as concentrated at specific points, which typically coincide with the floors of a building. This method is useful in dynamic analysis as it assumes high floor stiffness, enabling simpler models for understanding structural behavior under seismic forces.
Detailed
Detailed Summary
In structural engineering, especially in the context of dynamic analysis during seismic events, the concept of Lumped Mass Idealization (LMI) plays a crucial role. This idealization allows for the representation of a complex structure by simplifying its mass distribution into discrete points, typically at floor levels. This method proves effective in scenarios where the stiffness of the floors is significantly high, enabling engineers to reduce intricate models to simpler representations without losing essential behavioral insights. LMI finds application in several analyses, including modal analysis, time history analysis, and response spectrum analysis.
The justification for utilizing lumped mass models can be framed as follows:
* They simplify the analysis of complex structures.
* They allow for more accessible calculations and simulations in dynamic analysis.
* They provide a foundation for understanding the fundamental behaviors of structures under seismic loading.
Despite its advantages, engineers must ensure that the assumptions related to floor stiffness and rigidity are valid for the specific buildings in question, as this idealization could lead to oversights in dynamic responses for structures that do not adhere to these assumptions.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Concept of Lumped Mass Idealization
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
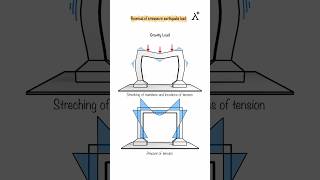
In real structures, mass is distributed throughout. For simplicity in dynamic analysis:
- Mass is assumed to be lumped at specific points (commonly at floor levels).
- Floors are assumed to be rigid in their own plane.
Detailed Explanation
In engineering, particularly when analyzing structures during dynamic events like earthquakes, simplifying complex systems helps us understand their behavior better. The Lumped Mass Idealization assumes that instead of having mass spread out over the entire structure, we can concentrate it at certain key points, which are often at the floors. This approach makes calculations easier and is practical because it also assumes that each floor is sufficiently stiff, or rigid, in terms of its own movement. This means that the effects of the mass can be treated as if it’s concentrated, simplifying how we analyze how a building will sway or respond under loads.
Examples & Analogies
Think of a multi-story building like a stack of books on a shelf. If each book represents the mass of a floor, rather than considering the whole weight of the books distributed evenly across the entire shelf, we treat each book as if it's a lump of weight that only rests on the shelf at one point (the floor level). This concentration makes it easier to calculate how much the shelf will bend or sway when you push down on it, similar to how we analyze buildings during an earthquake.
Justification for Lumped Mass Idealization
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Acceptable in buildings where floor stiffness is high.
- Allows reduction of complex systems to simpler models.
Detailed Explanation
The Lumped Mass Idealization works best in buildings that have strong, rigid floors. When the floors are stiff, they can effectively support the loads without deforming significantly, meaning the behavior of the structure can be modeled accurately with this simplification. Reducing a complex structure to a simpler model allows engineers to perform dynamic analysis without getting weighed down by unnecessary details, enabling quicker reactions and more efficient designs.
Examples & Analogies
Imagine driving a sports car with stiff suspension compared to a minivan with softer suspension. In a sports car, the way it absorbs bumps and handles turns can be accurately predicted by simplifying the model of the car’s movements. Similarly, in a solidly built high-rise building, we can confidently assume a lumped mass model because the floors don’t flex much under stress, just like how the sports car responds predictably.
Applications of Lumped Mass Models
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Lumped mass models are extensively used in:
- Modal analysis
- Time history analysis
- Response spectrum analysis
Detailed Explanation
Lumped mass models find their applications in various types of analyses used in earthquake engineering. In modal analysis, these models help determine the natural frequencies and mode shapes of structures, which are critical in understanding how they will respond to seismic activities. Time history analysis involves observing the structure's response over time against a record of ground motion, while response spectrum analysis allows engineers to visualize expected responses given various dynamic loads. All these methods benefit from the simplicity and clarity offered by lumped mass idealization.
Examples & Analogies
Consider how musicians use simplified sheet music during rehearsals to quickly understand the flow of a complex symphony. By focusing on the key melodies (analogous to structural responses), they can practice parts without getting bogged down in the detailed arrangements. Similarly, using lumped mass models in engineering enables a clear and focused analysis of structural behavior during earthquakes, allowing engineers to design safer buildings efficiently.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Lumped Mass Idealization: A modeling method that concentrates mass at discrete points for simplification.
-
Dynamic Analysis: Analyzing the behavior of structures under time-varying loads.
-
Modal Analysis: A way to analyze the natural frequencies of a structure.
-
Response Spectrum Analysis: A useful technique for assessing maximum structural responses under seismic actions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a five-story building, mass may be lumped at the roof and each floor level to analyze responses in a modal analysis efficiently.
-
In time history analysis, lumped mass models simplify the assessment of how each structural level interacts under seismic loads.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In buildings tall and smart, we lump the mass, that's the art! At each floor, the weight we place, so dynamic analysis has a pace.
📖 Fascinating Stories
-
Once upon a time, a wise engineer decided to simplify heavy structures. He found that by concentrating mass at floors, his analyses became easier and more effective—this method was known as Lumped Mass Idealization.
🧠 Other Memory Gems
-
MASS: M - Model Simplification, A - Allowing for Rigidity, S - Structural Analysis, S - Seismic Relevance.
🎯 Super Acronyms
LMI
- L: - Lumped
- M: - Mass
- I: - Idealization.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Lumped Mass Idealization
Definition:
A modeling technique that simplistically concentrates a structure's mass at discrete points, often at floor levels.
-
Term: Dynamic Analysis
Definition:
The study of structures subjected to dynamic loads, such as seismic forces, to understand their behavior under such conditions.
-
Term: Modal Analysis
Definition:
A method used to determine the natural vibration modes and frequencies of a structure.
-
Term: Response Spectrum Analysis
Definition:
An analytical technique used to summarize the maximum response of a structure subject to seismic excitations across a range of frequencies.
-
Term: Seismic Forces
Definition:
Forces induced in a structure as a result of ground motion during an earthquake.