Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Convolution Integral
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're discussing the convolution integral and how it applies to linear time-invariant systems. The convolution integral helps us understand how systems respond over time to inputs.
What exactly does convolution mean in this context?
Great question! Convolution basically combines two functions by integrating their product. In our case, we are comparing the impulse response function with the external force applied over time.
So, how do we mathematically express this?
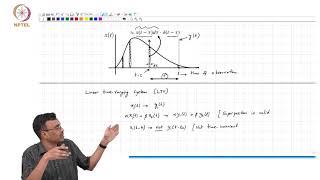
It's expressed as x(t) = ∫₀ˡh(t - τ)F(τ)dτ. This means the output at time t is a combination of past inputs influenced by the impulse response of the system.
Why do we need to focus on linear systems?
Because the principle of superposition, which states that the output for a combination of inputs is the sum of the individual outputs, only holds true for linear systems.
Does this mean we can't apply this to non-linear systems?
Exactly! Non-linear systems require different analysis methods. We'll cover those later in our course.
To summarize, the convolution integral allows us to analyze linear time-invariant systems by combining impulse responses with inputs, and superposition is a key aspect of this approach.
Applications of the Convolution Integral
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s explore the practical applications of the Duhamel integral. Can anyone think of where this would be useful?
Maybe in earthquake engineering?
Correct! In earthquake engineering, we use the Duhamel integral to model how structures respond to ground motion.
How do we get the ground motion into this integral?
Great follow-up! The ground motion provides the input force F(t), which we combine with the system's impulse response h(t) to assess how the structure will react.
What about systems that are not linear?
For non-linear systems, we rely on more complex techniques since the simple convolution approach does not apply.
To sum up, the Duhamel integral is invaluable in understanding and predicting structural responses in linear systems subjected to dynamic loads.
Understanding System Linearity
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's dive deeper into what we mean by system linearity. Who can explain this concept?
I think it means that the response of the system is proportional to the input, right?
Exactly! In a linear system, if you double the input, the output also doubles.
And if that's not true, then we have a non-linear system?
Correct! Non-linear systems can't be analyzed with the convolution integral because their outputs are not directly proportional to their inputs.
Does this apply to all systems?
Not at all! Many real-world systems exhibit non-linear behavior, especially under extreme conditions. That's why we focus on linear systems for our first analysis steps.
In summary, understanding and identifying whether a system is linear or non-linear is critical for effective analysis and choosing the right methods for solving problems.
Implications of Duhamel’s Integral beyond Structural Engineering
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
We've discussed structural applications, but can you think of other areas where the Duhamel integral is employed?
Maybe in signal processing?
Yes! In signal processing, we often use convolution to filter signals, which helps eliminate noise and improve clarity.
Isn't it also used in control systems?
Absolutely! The principles of linearity and the use of impulse responses are fundamental to designing effective control strategies.
So, it applies to more than just mechanical systems, right?
Correct! Convolution has broad applications across disciplines, highlighting its versatility as a mathematical tool.
To wrap up, understanding convolution’s applications extends beyond our immediate field and shows the interconnectedness of engineering concepts.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section delves into the Duhamel integral as a convolution integral applicable to linear time-invariant systems. It highlights the pivotal role of the impulse response function and the output's dependence on the input force. The significance of linearity is stressed, with implications for structural control and digital signal processing.
Detailed
Detailed Summary
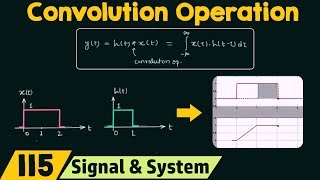
The convolution integral plays a critical role in characterizing the behavior of linear time-invariant (LTI) systems. This section introduces the Duhamel integral, which states that the output response of a system can be expressed as a convolution of the impulse response function, denoted as h(t), and the external input force, F(t). Mathematically, it is represented as:
$$ x(t) = \int_0^{t} h(t - \tau) F(\tau) d\tau $$
This formulation implies that the system's output is determined by the superposition of all past inputs, weighted by the system's impulse response at each interval.
The foundational concept of linearity is emphasized throughout this section. Since the principle of superposition must hold for the Duhamel integral to be valid, non-linear systems cannot be analyzed using this approach. The implications of this are far-reaching in various fields such as structural engineering, where understanding response dynamics under arbitrary loads is crucial.
In summary, the Duhamel integral and convolution integral serve as vital tools in engineering, helping to model responses in systems affected by time-variant forces while reinforcing the necessity of linearity for accurate analysis.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Convolution Integral
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Duhamel integral is a direct application of the convolution integral, which is valid only for linear time-invariant (LTI) systems.
Detailed Explanation
The Duhamel integral uses the concept of convolution to analyze how systems respond to inputs. Convolution integrates the effects of an entire input signal over time, weighted by the system's response to a unit impulse. This means if you know how the system behaves to a specific input, you can figure out its behavior for any arbitrary input by integrating over time. This method assumes the system's properties do not change over time, which is why it's specifically applicable to linear time-invariant systems.
Examples & Analogies
Imagine a sponge soaking up water. If you pour a steady stream of water onto it, the sponge reacts in a predictable way based on its size and material. Now, if you instead pour water in bursts or at intervals, the sponge's response – how much water it soaks up and how quickly – can still be understood if you know its response to a steady stream. This relationship across various inputs is similar to how convolution allows us to understand a system's response to different forces over time.
Mathematical Formulation of Convolution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The mathematical form of convolution: t x(t)=∫h(t−τ)F(τ)dτ 0
Detailed Explanation
This equation expresses the output x(t) at time t as an integral that combines the impulse response of the system h(t−τ) with the input function F(τ). The variable τ acts as a dummy variable that tracks the input force over time as it is applied. By integrating this product from time 0 to time t, we can find the total output of the system considering all previous inputs and how they influenced the current state.
Examples & Analogies
Think of a chef (the input force) making a soup (the system output). The chef adds ingredients (the impulse response) over time. The flavor of the soup at any given moment depends on all the ingredients added up to that point. If the chef adds a bit of spice, it influences the soup’s taste immediately and continuously until the soup is consumed. Just like the convolution integral considers the cumulative effect of all past inputs on the present output.
System Linearity and Superposition Principle
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The principle of superposition must hold, which is why this integral is not suitable for nonlinear systems.
Detailed Explanation
For the convolution integral to be valid, the principle of superposition must apply, meaning the response caused by multiple inputs can be added together to get the total response. In nonlinear systems, this principle breaks down because the response does not simply add up; interactions between inputs can create unpredictable results. This distinction is crucial in engineering and physics when determining which methods to use for analyzing systems under various conditions.
Examples & Analogies
Consider a light dimmer that increases illumination linearly relative to how far you turn it. If you turn it halfway, you get half the light. Now, imagine a more complex lighting system with various fixtures where turning one knob affects the brightness of another fixture in unexpected ways. This would be akin to a nonlinear system. In linear systems, we can confidently predict that mixing multiple light sources simply adds their brightness together, much like how convolution integrates responses in predictable, straightforward ways.
Applications Beyond Structural Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This foundational idea is also critical in structural control, digital signal processing, and filtering in vibration analysis.
Detailed Explanation
The concept of convolution is not limited to earthquake engineering; it finds extensive applications in various fields like digital signal processing (DSP), where it's used to filter signals and in structural control systems that manage vibrations in buildings. In DSP, for instance, convolution helps in smoothing signals by effectively 'blending' them with a designed filter response, leading to clearer sound or image formats. Understanding how different elements interact over time is vital in designing effective systems.
Examples & Analogies
Think of a barista creating a special coffee blend. The barista can mix various coffee extracts to create a unique drink. Each extract influences the final flavor based on when and how much was added, similar to how convolution captures the impact of each input on the total system output over time. In both cases, timing and the cumulative effect of inputs are key elements in crafting the final product.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Convolution Integral: A method used to compute the output response of LTI systems by integrating the product of the impulse response and the input function over time.
-
Principle of Superposition: The concept that the total output of a linear system is the sum of its responses to individual inputs.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
For an earthquake response analysis, we use the ground acceleration as F(t) in our convolution integral to determine how the structure will react over time.
-
The impulse response function h(t) can be derived from the system's characteristics and is then used in the convolution process for predicting system behavior.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Con-o-lution, oh what a treat, it helps us decide on how inputs meet!
📖 Fascinating Stories
-
Imagine a chef mixing ingredients for a cake. Each ingredient's effect is like an impulse response, creating a unique flavor depending on how they blend together, just like the convolution integral does with inputs.
🧠 Other Memory Gems
-
For the Duhamel integral, remember Depends on impulse response and Integrates inputs to Evaluate outputs: 'DIE'.
🎯 Super Acronyms
LTI = **L**inear, **T**ime **I**nvariant for system analysis - remember LTI!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Convolution Integral
Definition:
A mathematical operation used to express the output of an LTI system as a weighted sum of past inputs using the impulse response function.
-
Term: Impulse Response Function
Definition:
The output response of an LTI system when subjected to a unit impulse force.
-
Term: Linear TimeInvariant (LTI) System
Definition:
A system characterized by linearity and time invariance, allowing the output to be computed as a convolution of input and system response.
-
Term: Principle of Superposition
Definition:
A principle stating that the response caused by two or more inputs applied to a linear system equals the sum of the responses that would have been caused by each input separately.
-
Term: Nonlinear Systems
Definition:
Systems where the output is not directly proportional to the input, making them unsuitable for analysis via the convolution integral.